A rod of mass and resistance is placed on fixed, resistanceless, smooth conducting rails (closed by a resistance ) and it is projected with an initial velocity .Find its velocity as a function of time.

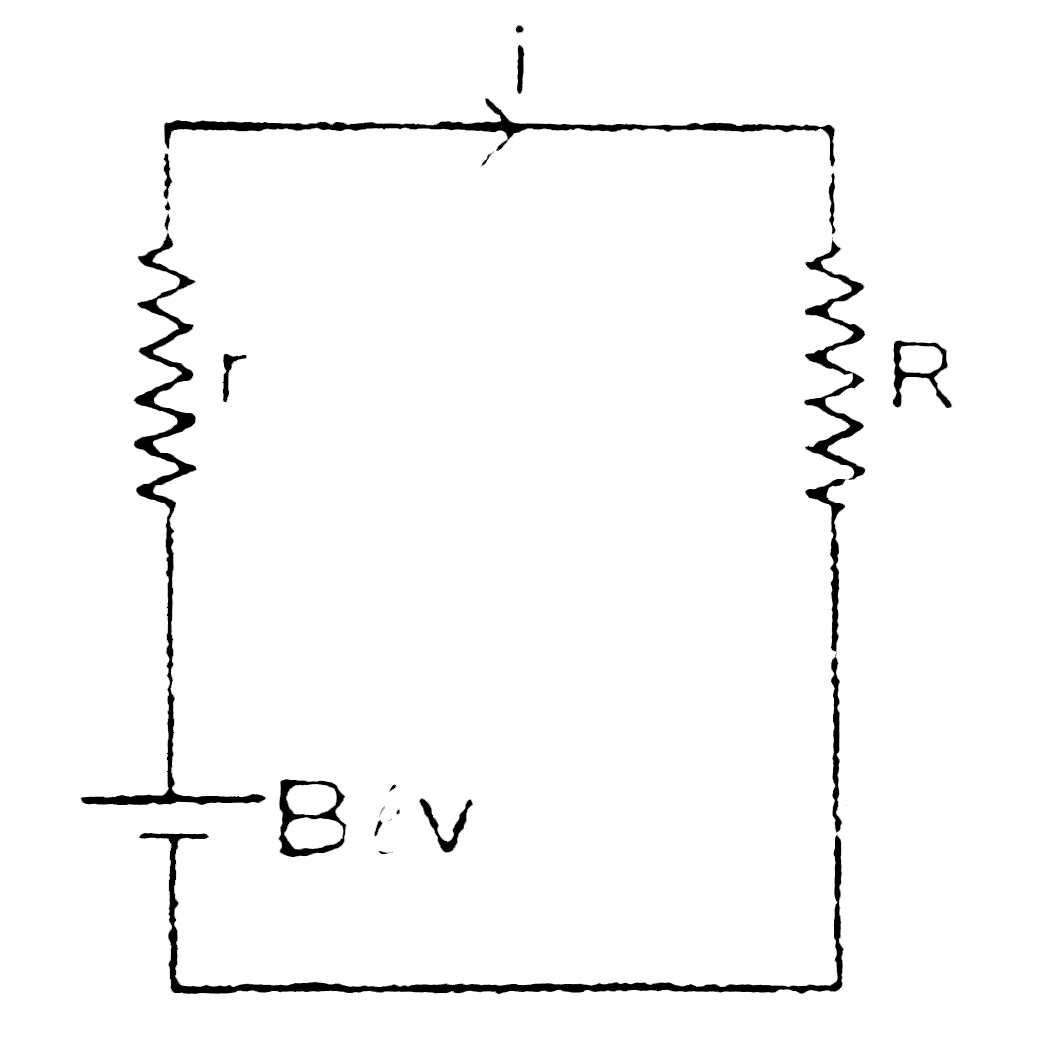
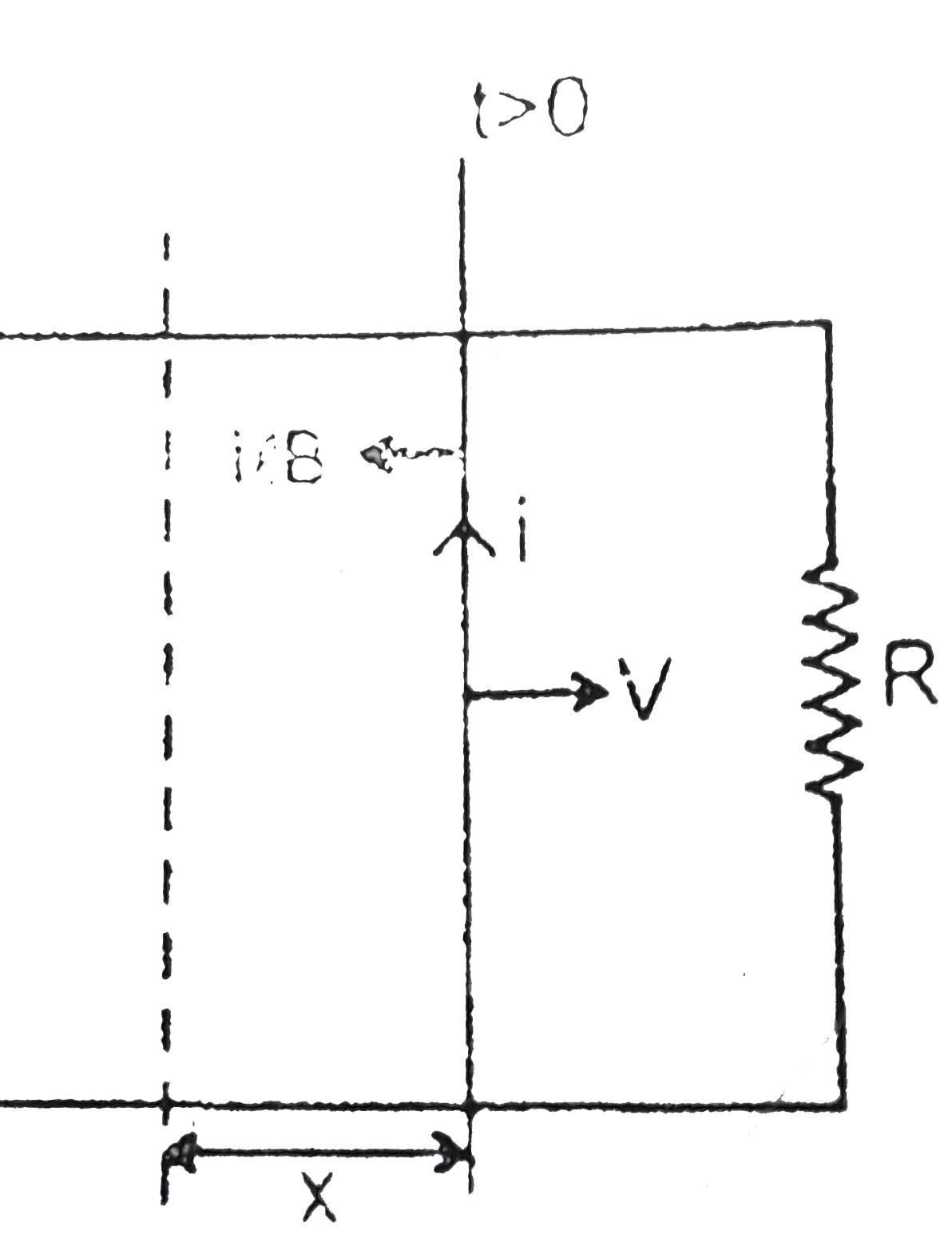
Let at an instant the velocity of the rod be .The induced in the rod will be .The electrically equivalent circuit is shown in the following diagram.
Current in the circuit
At time
Magnetic force acting on the rod is opposite to the motion of the rod.
..(1)
..(2)
Now solving these two equation
let
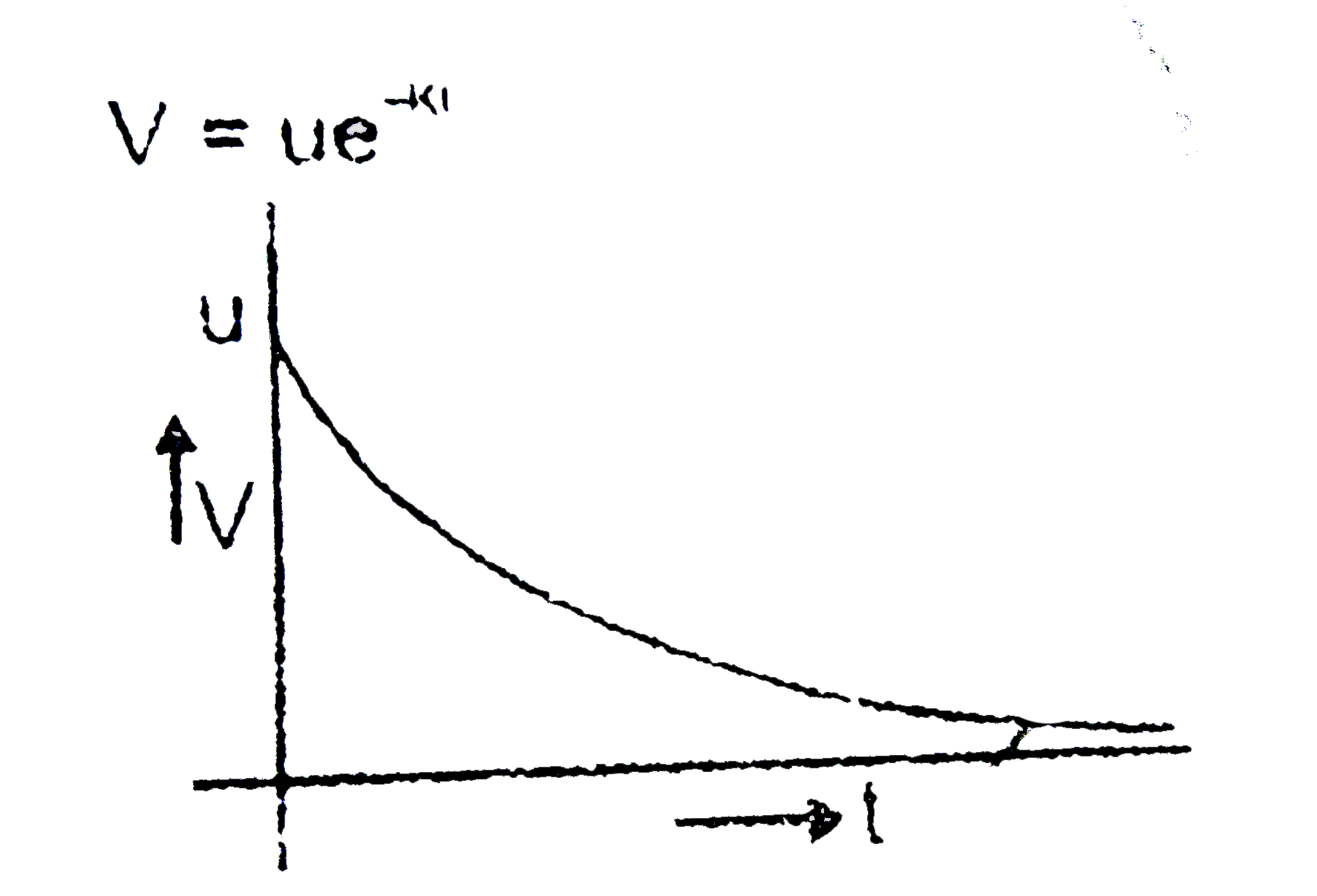
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Problem
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-1
Explore 63 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:HLP
Explore 39 Videos
Similar Questions
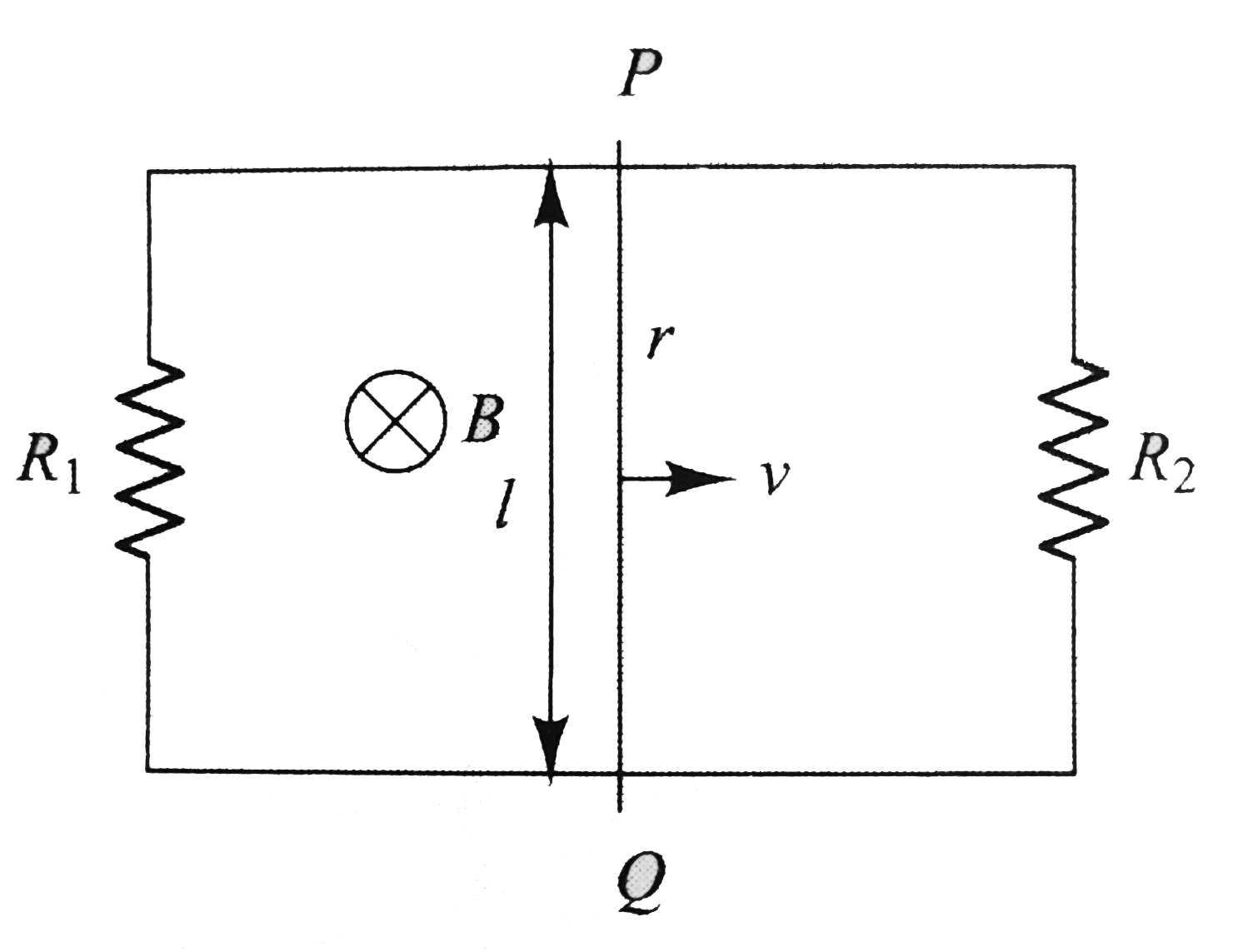
Shows rod PQ of mass m and resistance r moving on two fixed, resistanceless, smooth conducting rails (closed on both sides by resistances R1andR2). Find the current in the rod (at the instant its velocity is v).
View SolutionIn the figure shown PQRS is a fixed resistanceless conducting frame in a uniform and constant magnetic field of strength B. A rod EF of mass m length l and resistance R can smoothly move on this frame.A capacitor charged to a potential difference V0 initially is connected as shown in the figure.Find the velocity of the rod as function of time t if it is released at t=0 from rest.
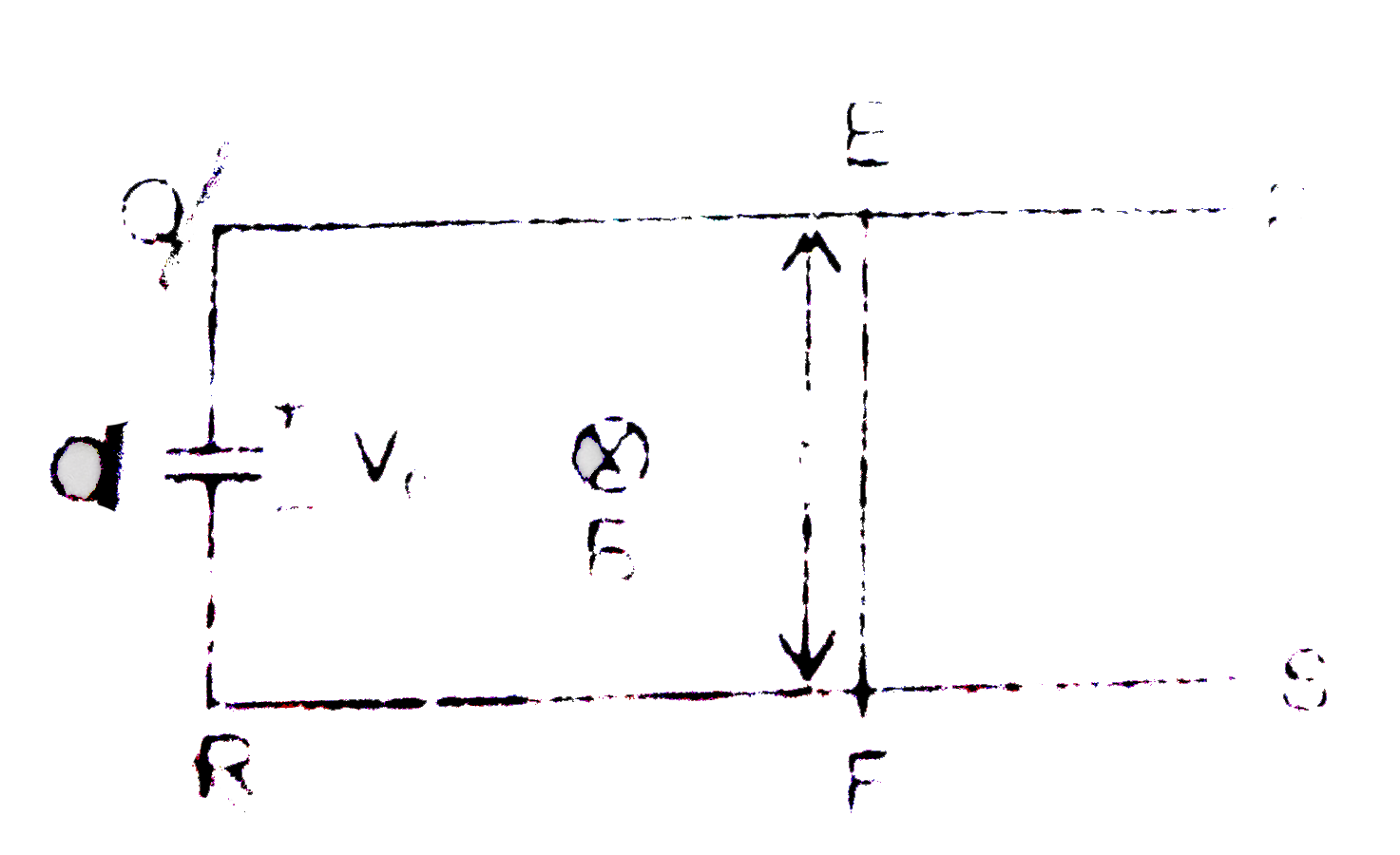
View Solution
Knowledge Check
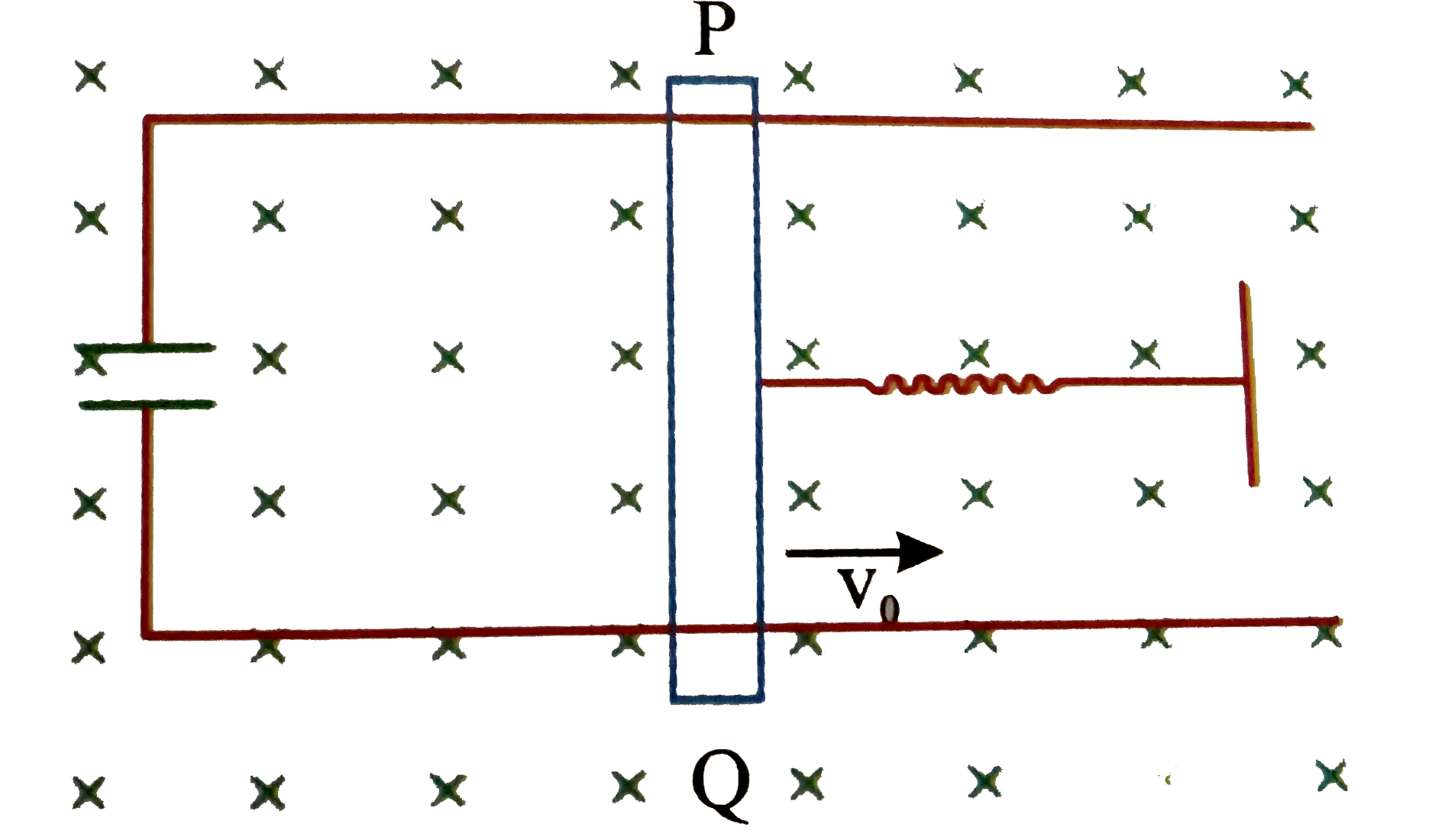
A conducting rod PQ of mass m and length l is placed on two long parallel (smooth and conducting) rails connected to a capacitor as shown. The rod PQ is connected to a non conducting spring of spring constant k, which is initially in relaxed state. The entire arrangement is placed in a magnetic feild perpendicular to the plane of figure.
Neglect the resistance of the rails and rod.
Now, the rod is imparted a velocity v0 towards right, then acceleration of the rod as a function of its displacement x given by
 AkxmBkxm+B2l2CCkxm−B2l2CDkxB2l2C
AkxmBkxm+B2l2CCkxm−B2l2CDkxB2l2C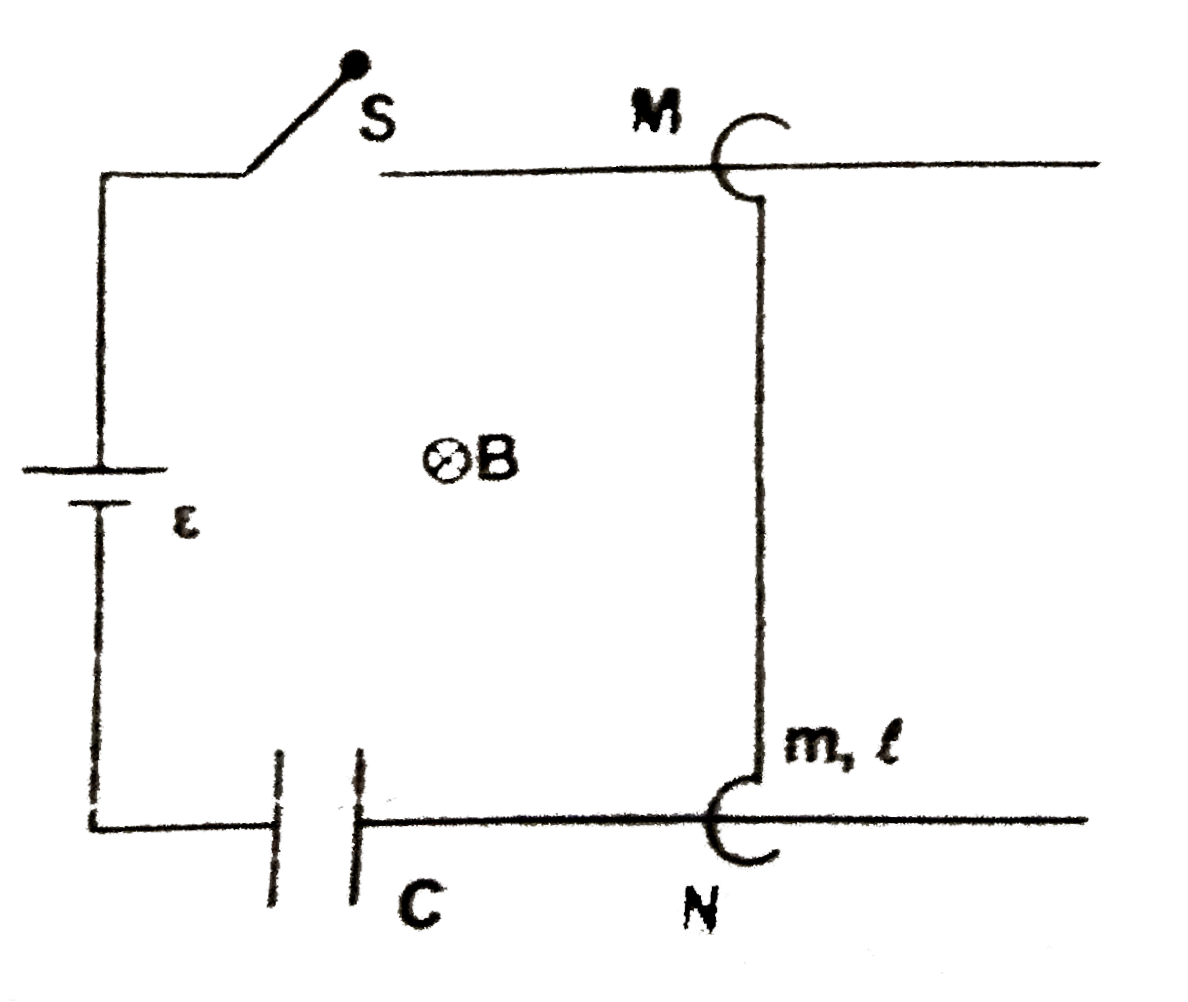
A conducting rod MN of mass m and length 'l' is placed on parallel smooth conducting rails connected to an uncharged capacitor of capacitance C and a battery of emf ε as shown. A uniform magnetic field B is existing perpendicular to the plane of the rails. The steady state velocity acquired by the conducting rod MN after closing switch S is (neglect the resistance of the parallel rails and the conducting rod)A2CBlε(m+CB2l2)BCBlε(m+CB2l2)CCBlε2(m+CB2l2)DCBlε4(m+CB2l2)A particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
A2usinαgB2u2sinαgCusinαgDu2sinαg
A uniform rod AB of mass m and length l is placed over two smooth conducting rails P and Q. If the witch shown as closed at t=0, find the velocity of rod AB as a function of time.
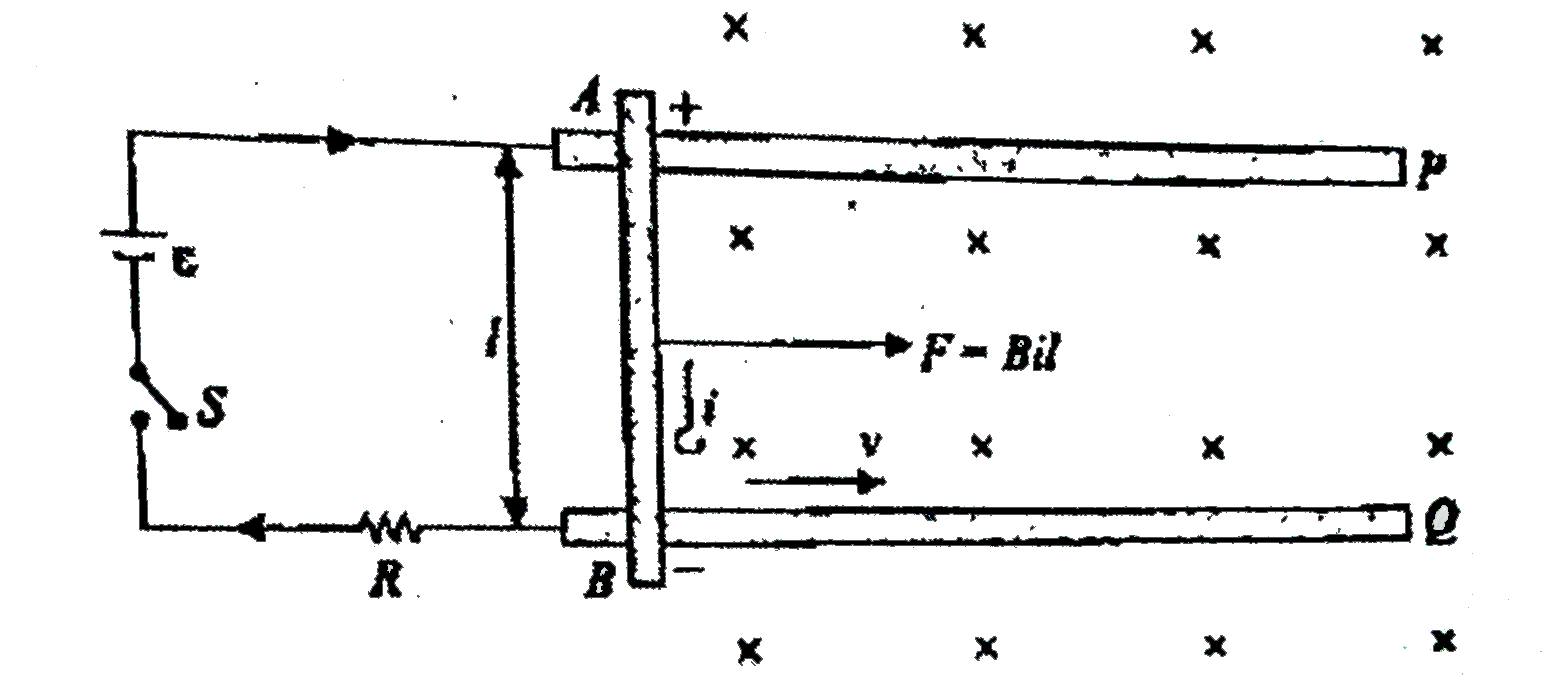
View SolutionA rod of mass m and resistnce R sldes on frictionless and resistanceless rails a distance l a part thast innclude a source of emf E0 (see figure). The rod is initially at rest. Find the expression for the
a. Velocity of the rod v(t). b. current in the loop i(t).
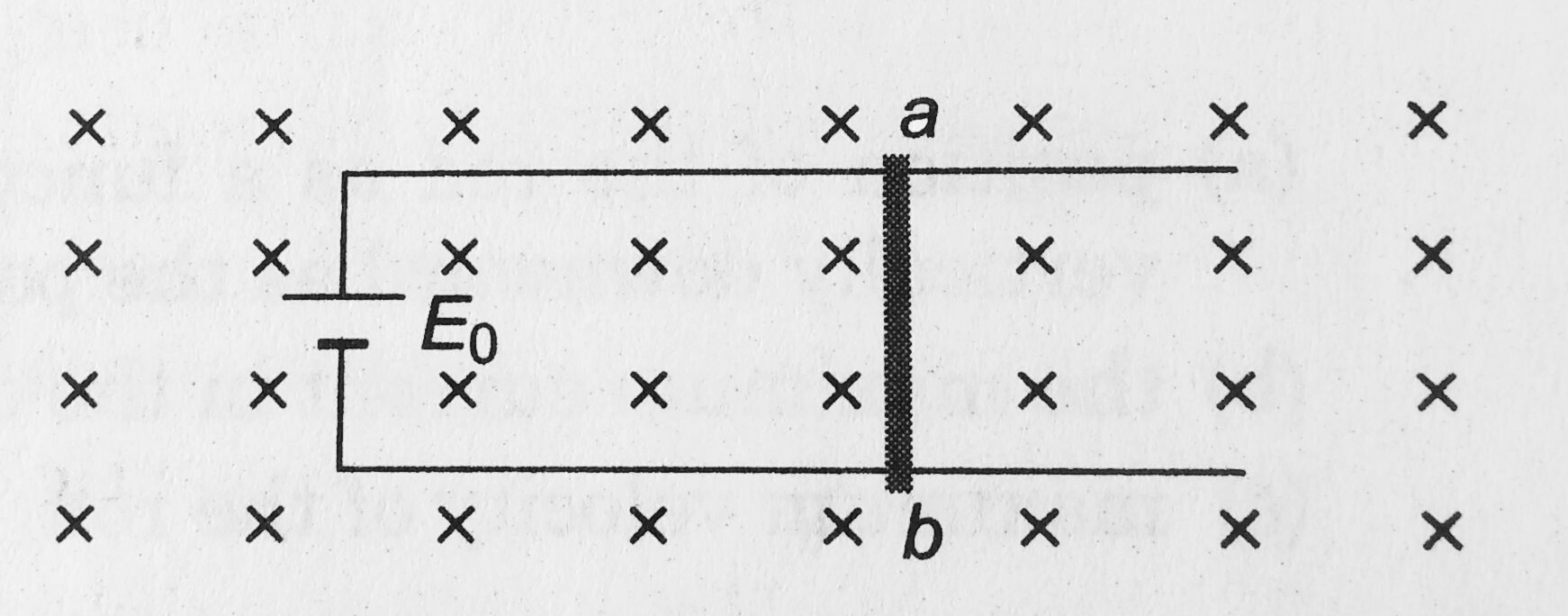
View SolutionIn the figure shown a conducting rod of length l, resistance R and mass m is moved with a constant velocity v. The magnitude field B varies with time t as B=5t, what t is time in second. At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged. the rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance. Find the current in the circuit as a function of time t.
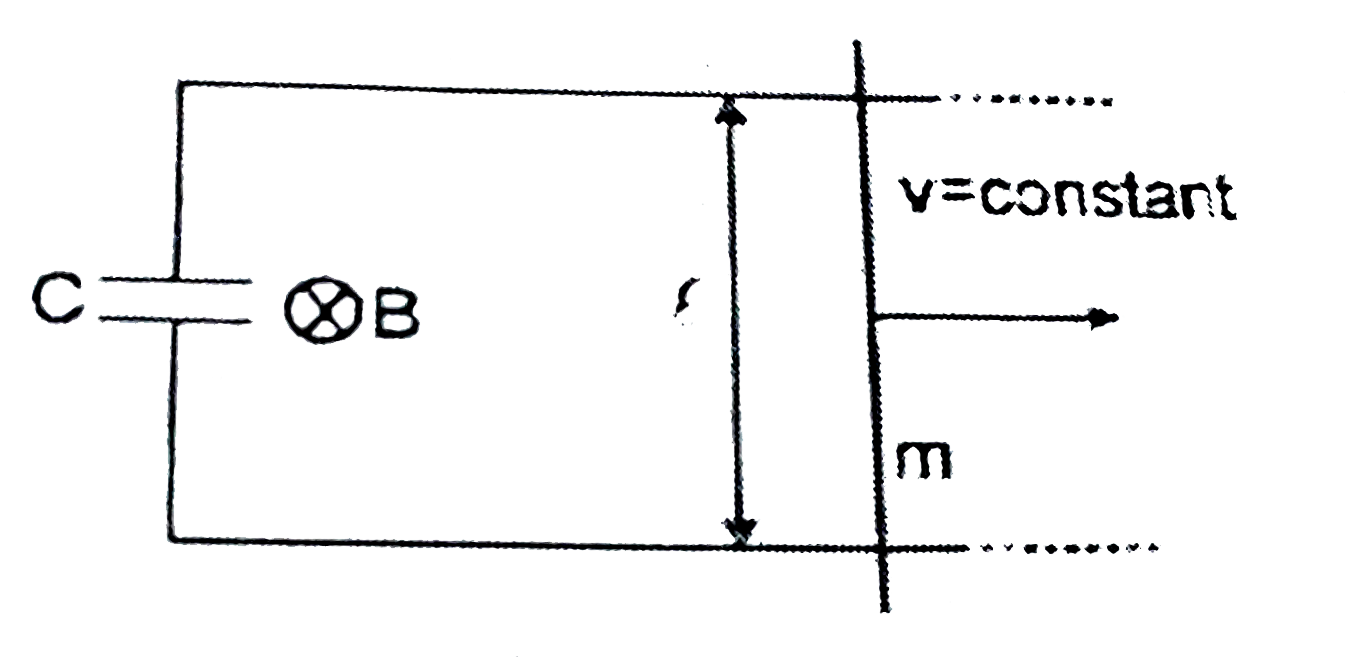
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
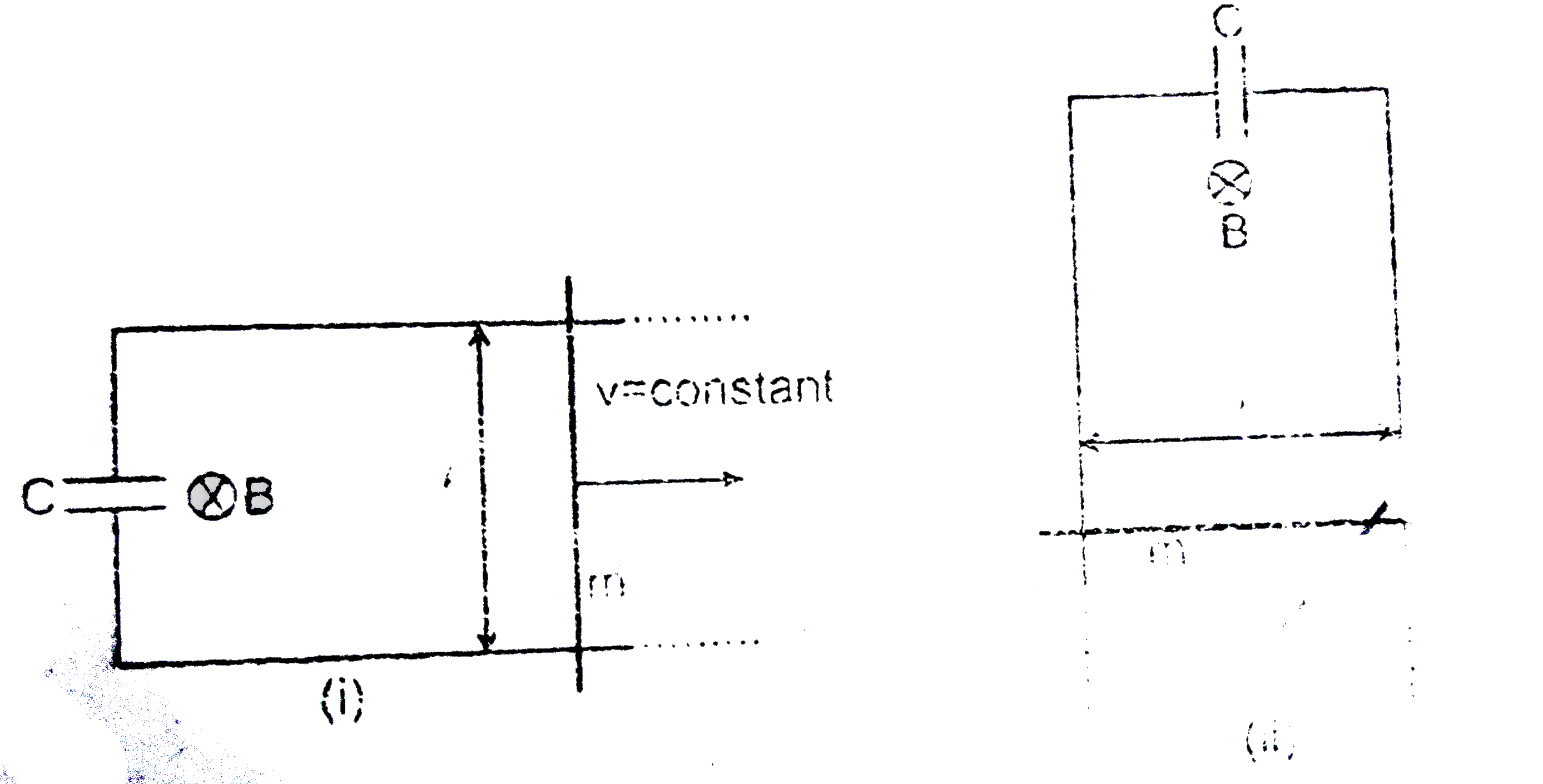
View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
View Solution
