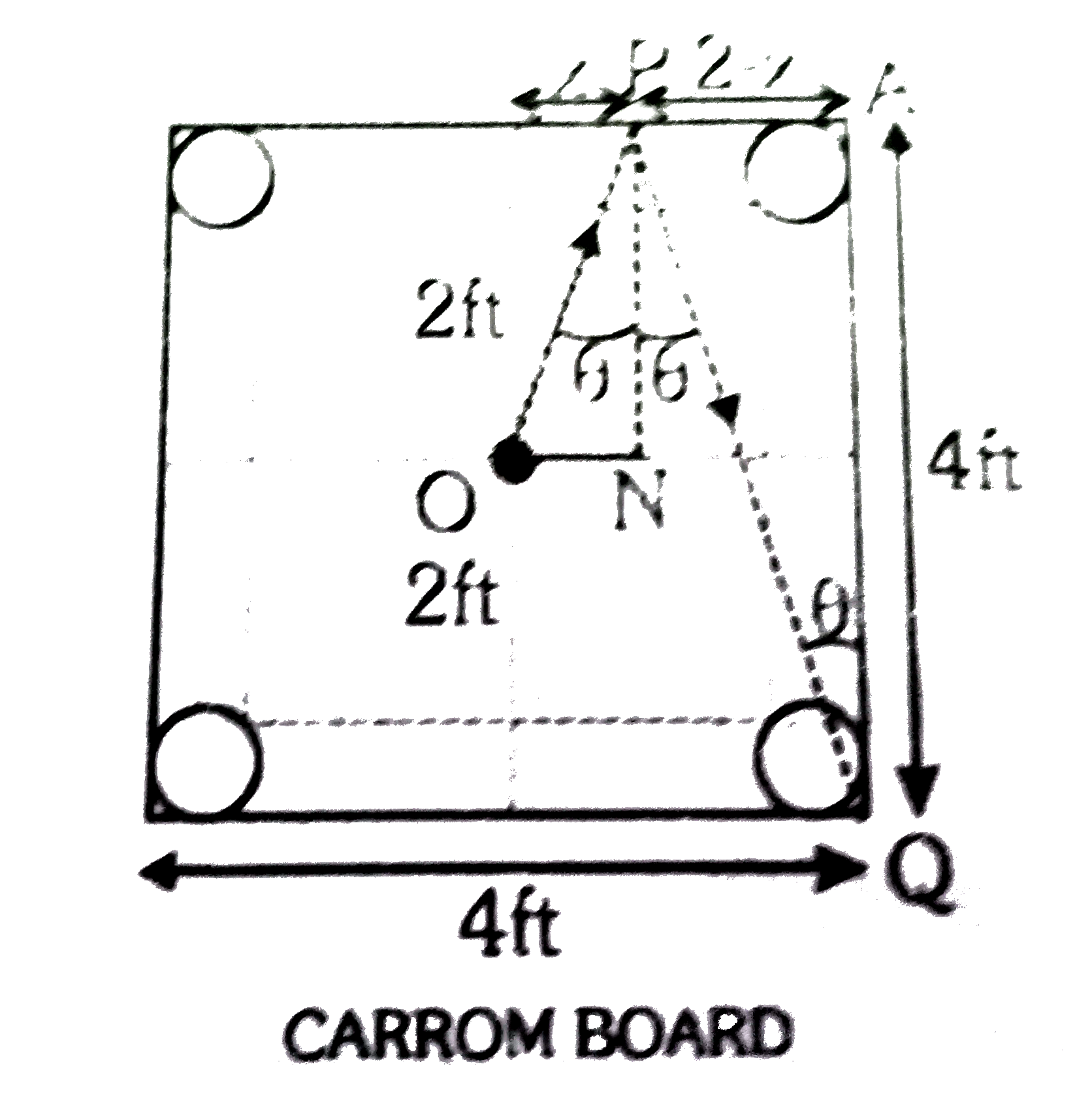
A carrom board 4ft×4ft square has the queen at the centre. The queen hit by the striker moves to the front edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen (a). from the centre to the front edge (b). from the front edge to the hole and (c). from the centre to the hole.
Compare triangle PAQ and ONP
tanθ=2−x4=x2⇒4−2x=4x
∴=46=23 ft.
In DeltaOPN OP=sqrt(ON^(2)+PN^(2))=sqrt(((2)/(3))^(2)+(2)^(2))=sqrt((40)/(9))=(2)/(3)sqrt(10)ft.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-199videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2170videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
A carrom board 4ft×4ft□) has the queen at the centre. The queen hit by the striker moves to the front edge, rebounds and goes in te hole behind the striking line. Find the magnitude of displacement of the queen a. from the centre to the front edge b. from teh front edge to teh hole and c. from the centre to teh hole.
View SolutionA square hole is punched out of a circular lamina, the diagonal of the square being the radius of the circle. If 'a' be the diameter of the sircle, find the distance of centre of mass of the remainder from the centre of the circle.
View Solution
Knowledge Check
- Question 1 - Select One
A square hole is punched out of a circular lamina of diameter a. The diagonal of the square is equal to the radius of the circle and one of the corners is at the centre of the circle . The distance of the C.G. of the remainder from the centre of circle is
Aa8π+4Ba8π−4Ca5π−4Da5π+4 - Question 2 - Select One
A square hole is punched out of a circular lamina of diameter 4 cms., the diagonal of the square being a radius of the circle. Centroid of the remainder from the centre of the circle is at a distance
A12π+1B12π−1C1π+1D1π−1
A mosquito net over a 7ft×4ft bed is 3 ft high. The net hs a hole at one corner of the bed through which diagonally opposite upper corner of the net. A. Find the magnitude of the displaceentof the mosquito. B. Taking the hole as the origin, the length of the bed as the X-axis, its width as teh Y-axis, and verticallup as the Z-axis, write the components of the displacement vector.
View SolutionFind the centre of mass of a unifrom disc of radius a from which a circulr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
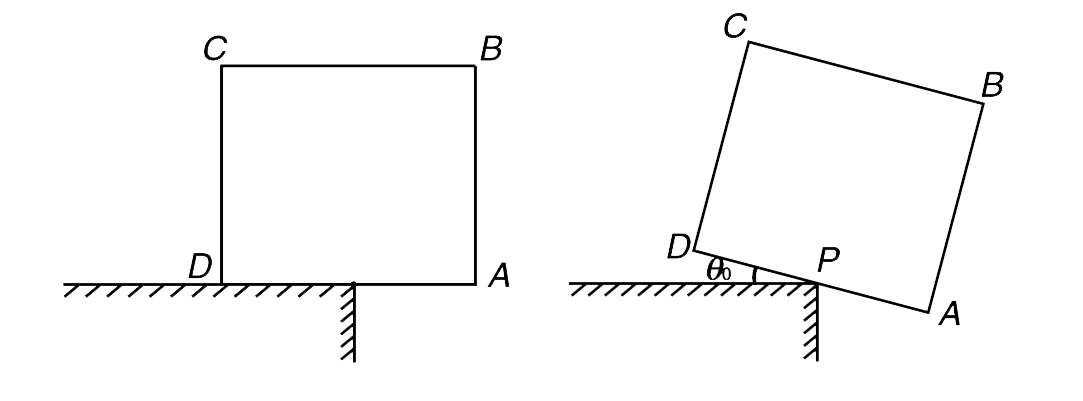
View SolutionA uniform cube of mass M and side length a is placed at rest at the edge of a table. With half of the cube overhanging from the table, the cube begins to roll off the edge. There is sufficient friction at the edge so that the cube does not slip at the edge of the table. Find -
(a) the angle θ0 through which the cube rotates before it leaves contact with the table.
(b) the speed of the centre of the cube at the instant it breaks off the table.
(c) the rotational kinetic energy of the cube at the instant its face AB becomes horizontal.
 View Solution
View SolutionA queen is placed at the centre of carom-board which has side of length a . It is hit from a position with a striker such that after rebounding from the front end, it goes into the hole in the opposite end. Find the distance traveled by the queen
View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View SolutionA disc of radius R is placed on a square plate of edge 4R made up of the same sheet with their planes parallel such that any two adjacent sides ofsquare touch the disc. Find the distance of the centre of mass of the system from the centre of square plate?
View Solution

