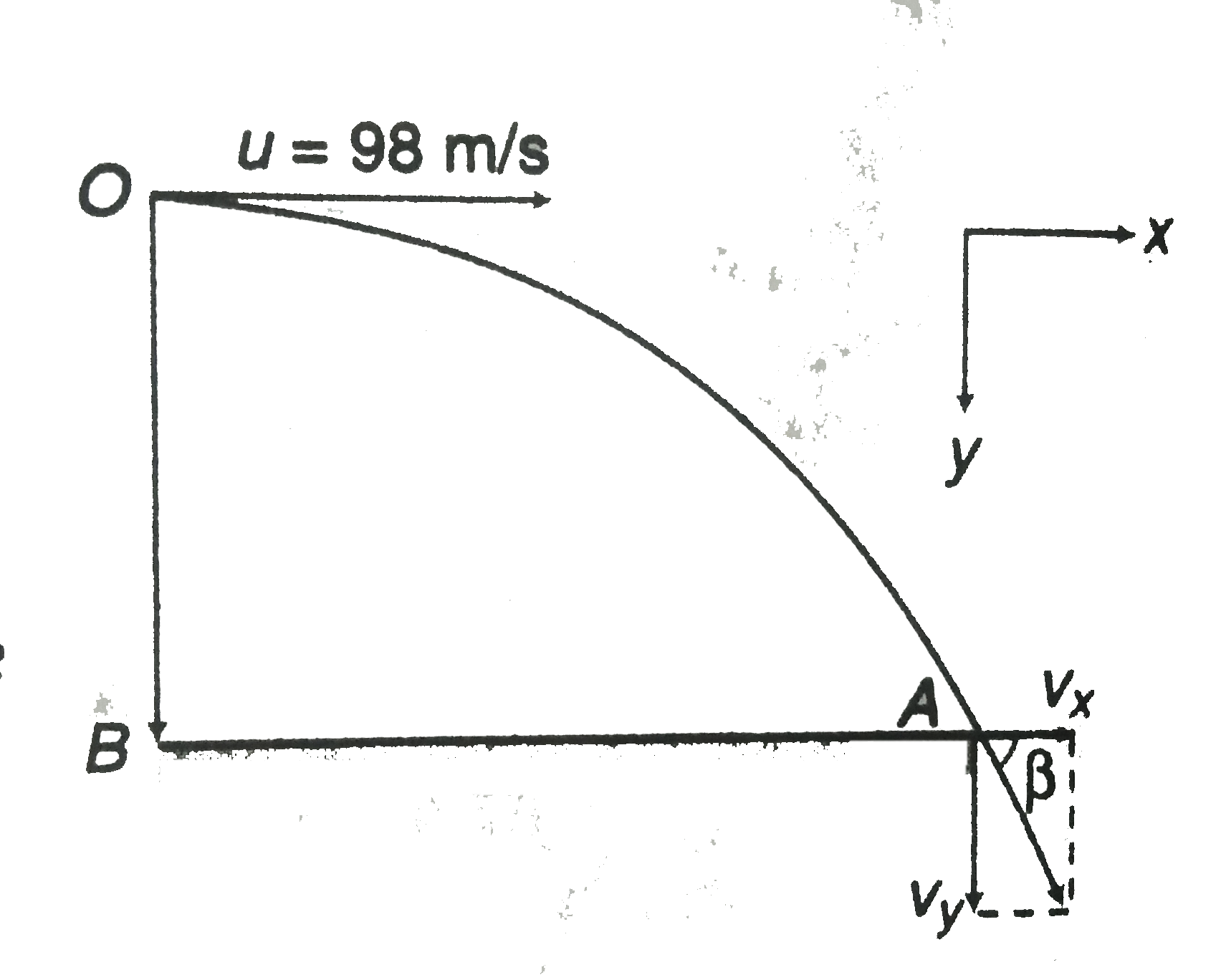
A projectile is fired horizontally with a velocity of $98 m s^{- 1}$ from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.

Video Solution

Text Solution

Verified by Experts

(i) The projectile is fired from the top O of a hill with velocity $u = 98 m s^{1}$ along the horizontal OX. It reaches the target P in vertical distance,
OA=y=490m
As $y = \frac{1}{2} {gt}^{2}$
$∴ 490 = \frac{1}{2} \times 9.8 t^{2}$
or $t = \sqrt{100} = 10 s$ .
(ii) Distance of the target from the hill is
AP=x=horizontal velocity xxtime=98xx10=980m.
(iii) The horizontal components of velocity v of the projectile at point P is $v_{x} = u = 98 m s^{- 1}$
$v_{x} = u_{y} + \geq 0 + 9.8 \times 10 = 98 m s^{- 1}$ and vertical component
$∴ v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{98^{2} + 98^{2}} = 98 \sqrt{2} = 138.59 m s^{- 1}$
Now if the resultant velocity v makes angle $β$ with the horizontal, then
$tan β = \frac{v_{y}}{v_{x}} = \frac{98}{98} = 1$ or $β = 45^{\circ}$

Updated on:21/07/2023

A projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. $(g = 9.8 m / s^{2})$
.
A $12 s$ , $980 m$ , $98 (\sqrt{2}) m / s$ $β = 45$
B $10 s$ , $98 m$ , $98 (\sqrt{2}) m / s$ $β = 45$
C $10 s$ , $980 m$ , $98 m / s$ $β = 45$
D $10 s$ , $980 m$ , $98 (\sqrt{2}) m / s$ $β = 45$
A stone is thrown horizontally with velocity $g m s^{- 1}$ from the top of a tower of height $g$ metre. The velocity with which it hits the ground is $(in m s^{- 1})$
A $g$
B $2 g$
C $\sqrt{3} g$
D $4 g$