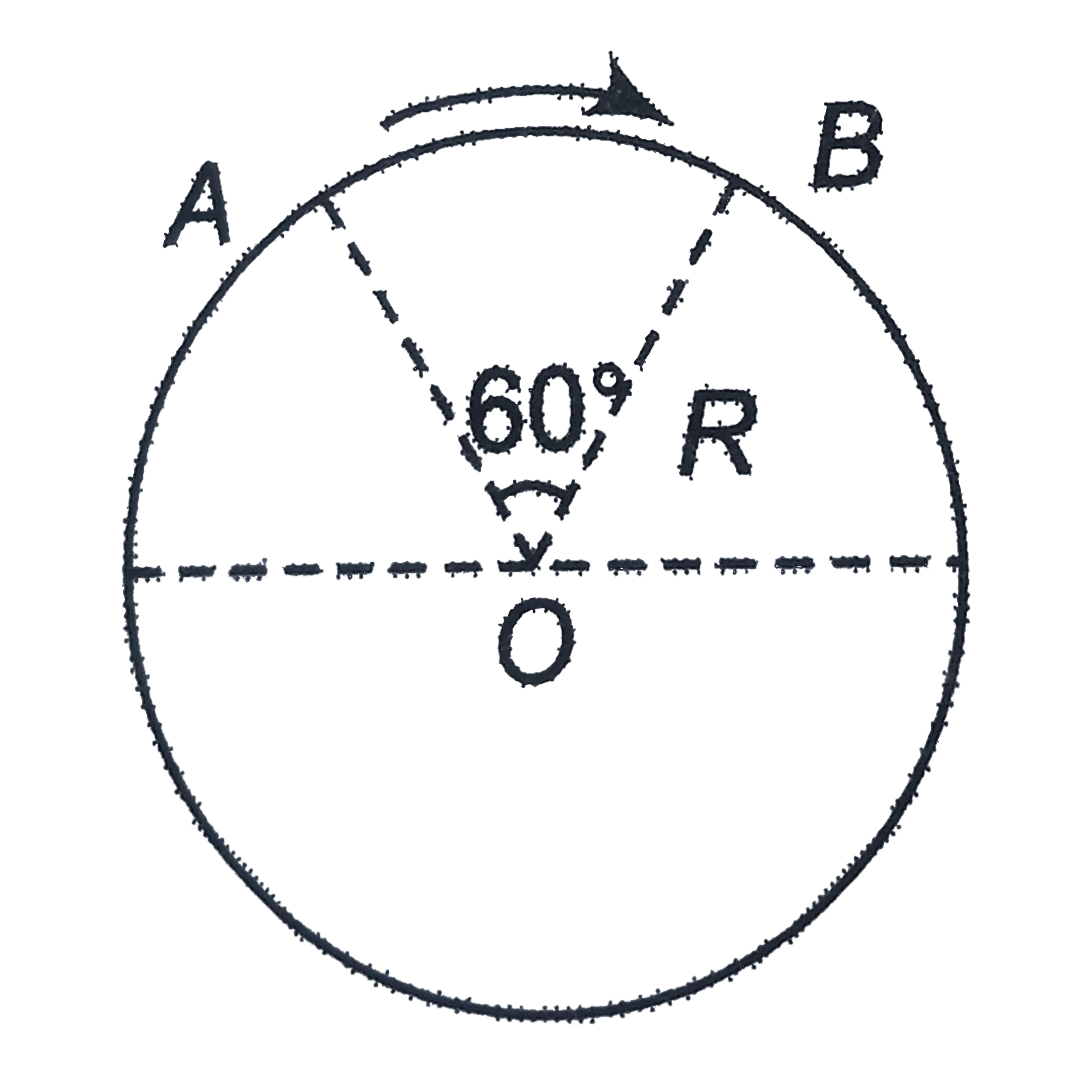
A particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
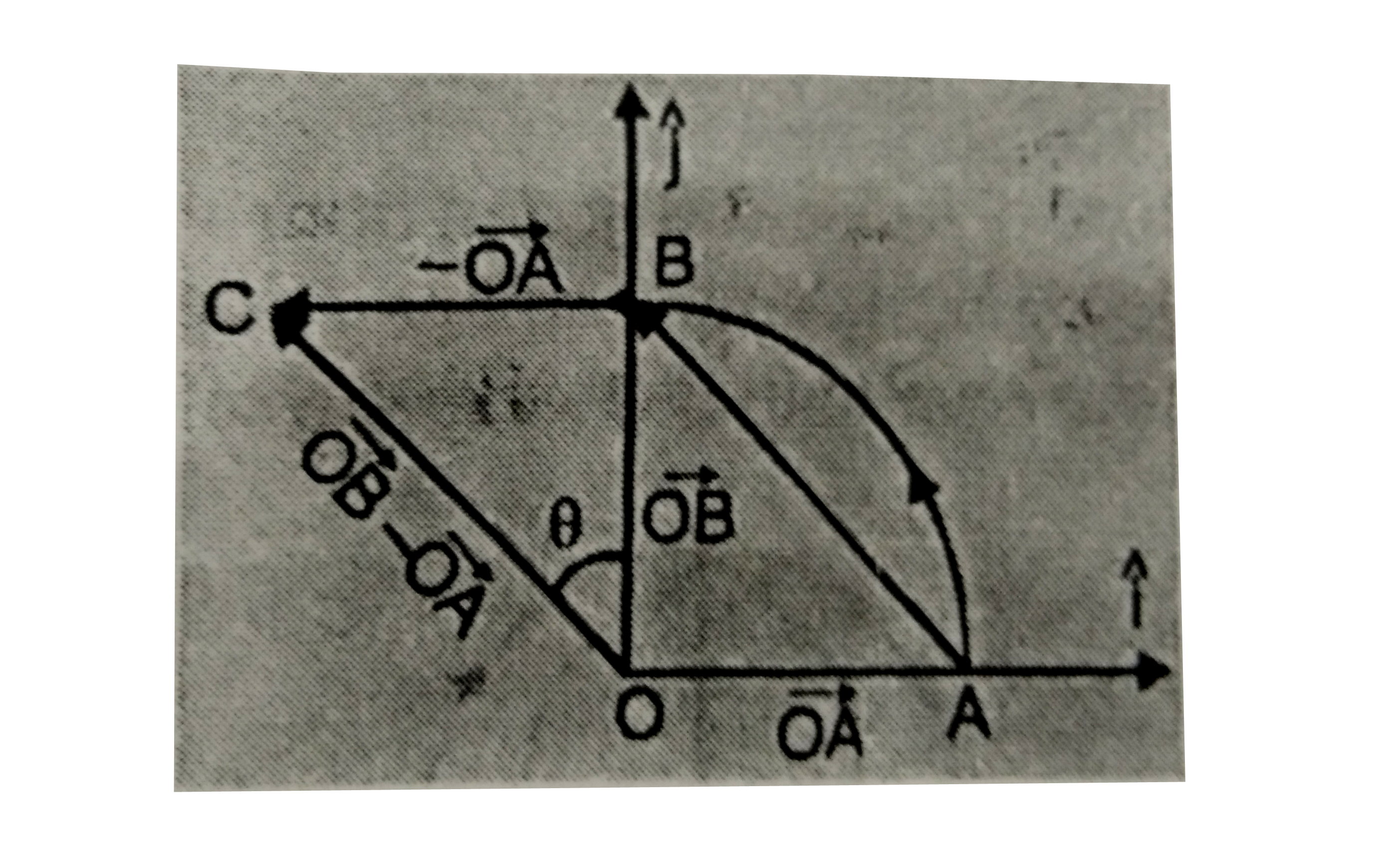
Displacement →AB=→OB−→OA=10ˆj−10ˆi
∣∣→AB∣∣=√102+102=10√2m
From ΔQABtanθ=OAOB=1010=1⇒θ=45∘
Angle between displacement vector →AB and x-axis =90∘C+45∘=135∘
Distance of path AB=14 (circumference) =14(2πR)m=(5π)m

Topper's Solved these Questions
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-1
Explore 99 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-2
Explore 170 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
Similar Questions
Knowledge Check
A particle travels from A to B path shown in figure, then the displacement of particle is :
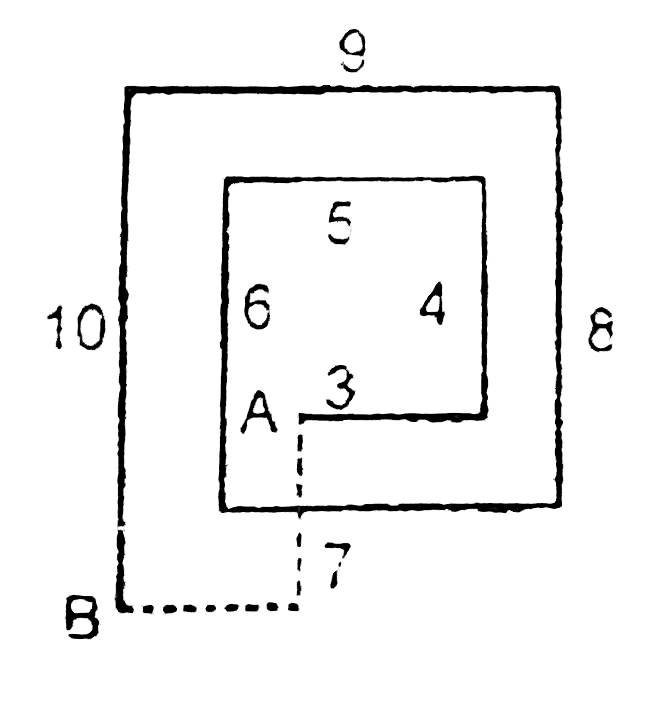 .A2√2mB4√2mC52mDnone of these
.A2√2mB4√2mC52mDnone of theseA particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.
 Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2A body moves along a quadrant of a circle of radius (r). The displacement and distance traveled are.
Ar√2,πr/2Br2πrC2√2r,πrDr1πr/2
A particle moves along an arc of a circle of radius R according to the law l=asinωt, where l is the displacement from the initial position measured along the arc, and a and ω are constants. Assuming R=1.00m, a=0.80m, and ω=2.00rad/s, find:
(a) the magnitude of the total acceleration of the particle at the points l=0 and l=±a,
(b) the minimum value of the total acceleration wmin and the corresponding displacement lm.
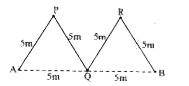
View SolutionFind the distance and displacement if the body moves from A to B along the path APQRB.
View SolutionA particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View Solution