A particle moves in a of radius R from A to B, as shown in the figure. Find the distance and displacement covered.
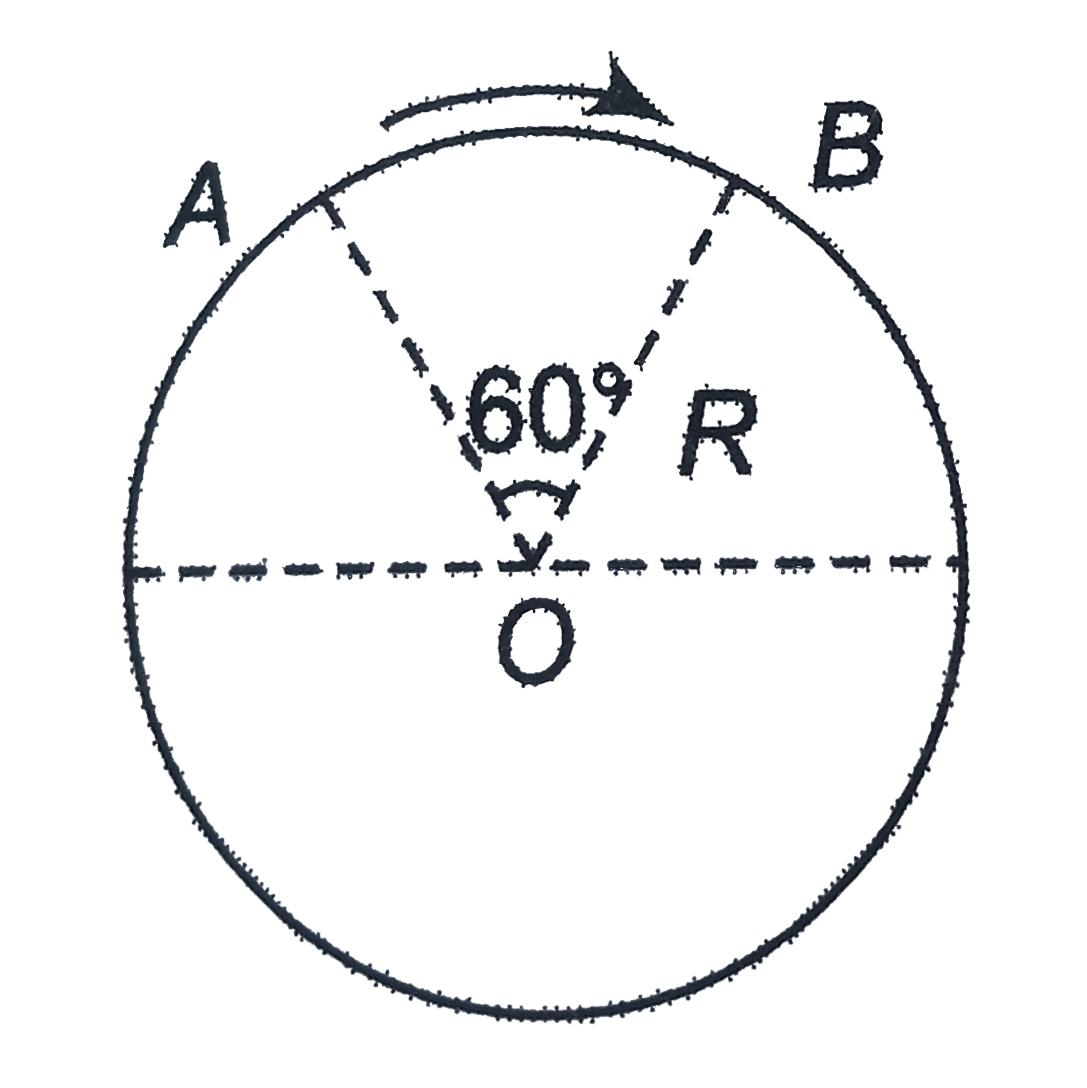
Distance =Length AB=2πR×60360=πR3
For displacement join A and B by a straight line and the length of this line is displacement.
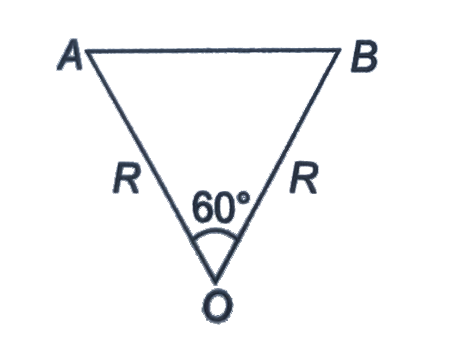
OA=OB=Radius=R
∠OAB=∠OBA=60∘
Hence, AB=Displacement=R
Topper's Solved these Questions
Similar Questions
A particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
View SolutionA person walks along a semicircular path from A to B as shown in the figure given below.
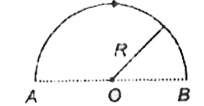
Calculate the distance and displacement traversed by the person.
View Solution
Knowledge Check
A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:
 A10mB5√2mC9mD7√2m
A10mB5√2mC9mD7√2mA particle travels from A to B path shown in figure, then the displacement of particle is :
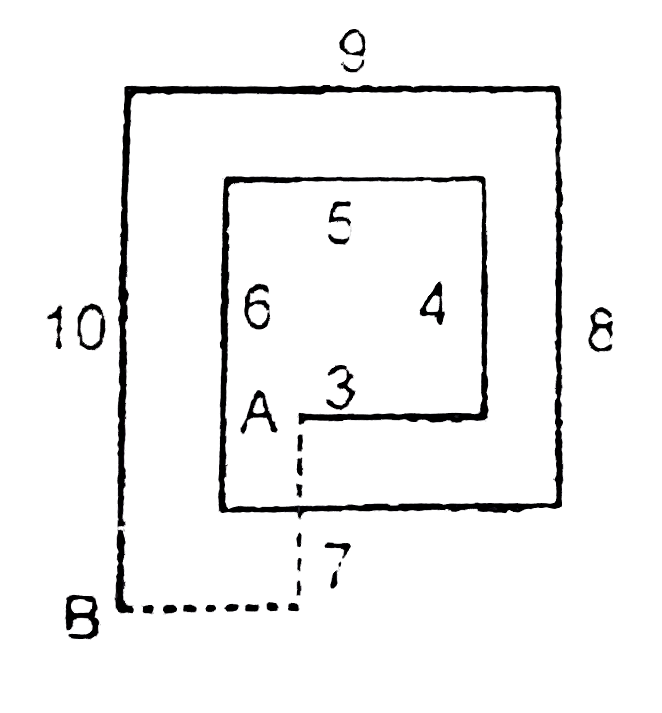 .A2√2mB4√2mC52mDnone of these
.A2√2mB4√2mC52mDnone of theseA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
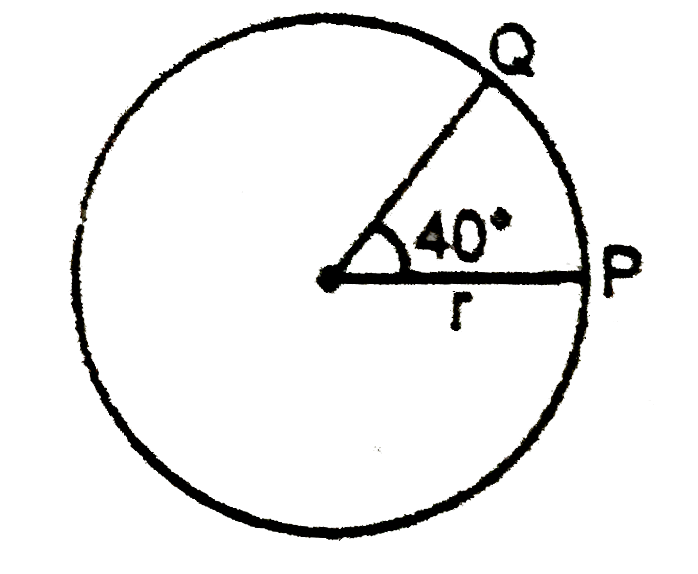 A2vcos40∘B2vsin20∘C2vcos20∘Dnone of these
A2vcos40∘B2vsin20∘C2vcos20∘Dnone of these
The velocity of a particle moving along a straight line varies with time as shown in the Figure. Find the total distance covered and the total displacement between 0 and 20 seconds.
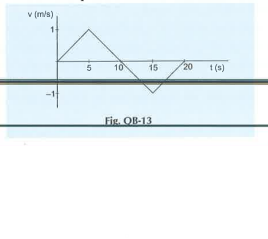
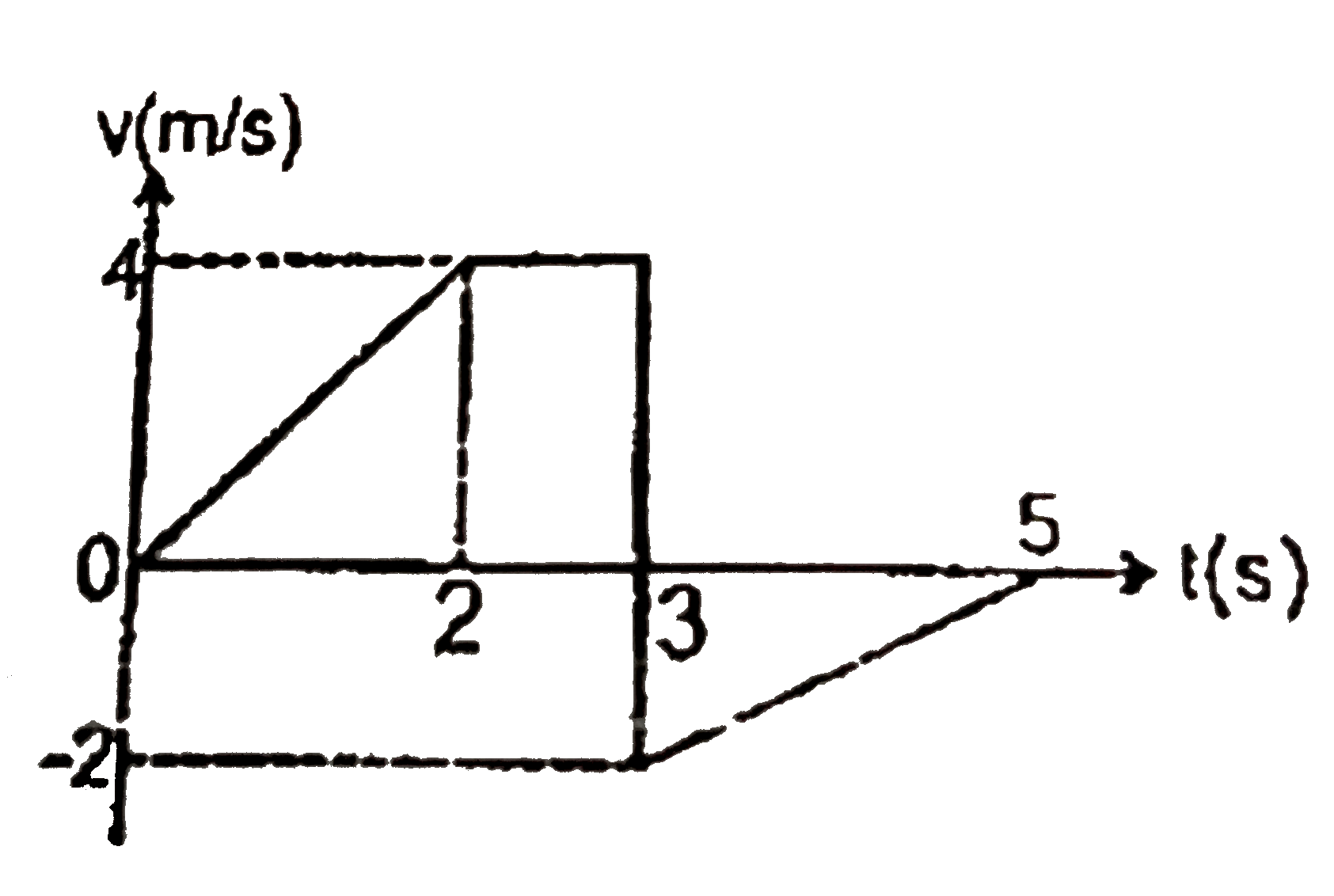
View SolutionFor a particle moving along x-axis, velocity-time graph is as shown in figure. Find the displacement of the particle?
View SolutionA person moves on a track ABC as shown in figure (∠B=90∘). Find distance and magnitude of displacement.
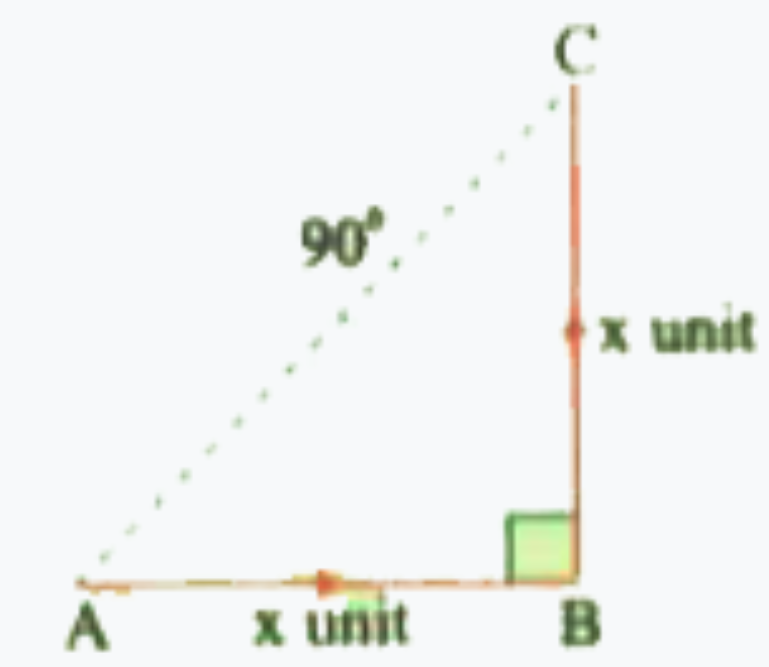
View SolutionA particle is moving in anticlockwise direction along a circle of radius R.
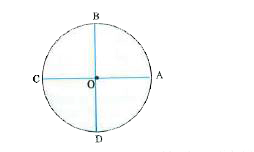
Calculate the distance and displacement covered by the particle (i) from A to C (ii) from A to D.
View SolutionA particle moves in a circle of radius R. In half the period of revolution its displacement is ………… and distance covered is ………. .
View Solution

