Show that [(p∨q)∨r]↔[p∨(q∨r)] is a tautology
Video Solution
Text Solution
Truth table of [(p∨q)∨r]↔[p∨(q∨r)]
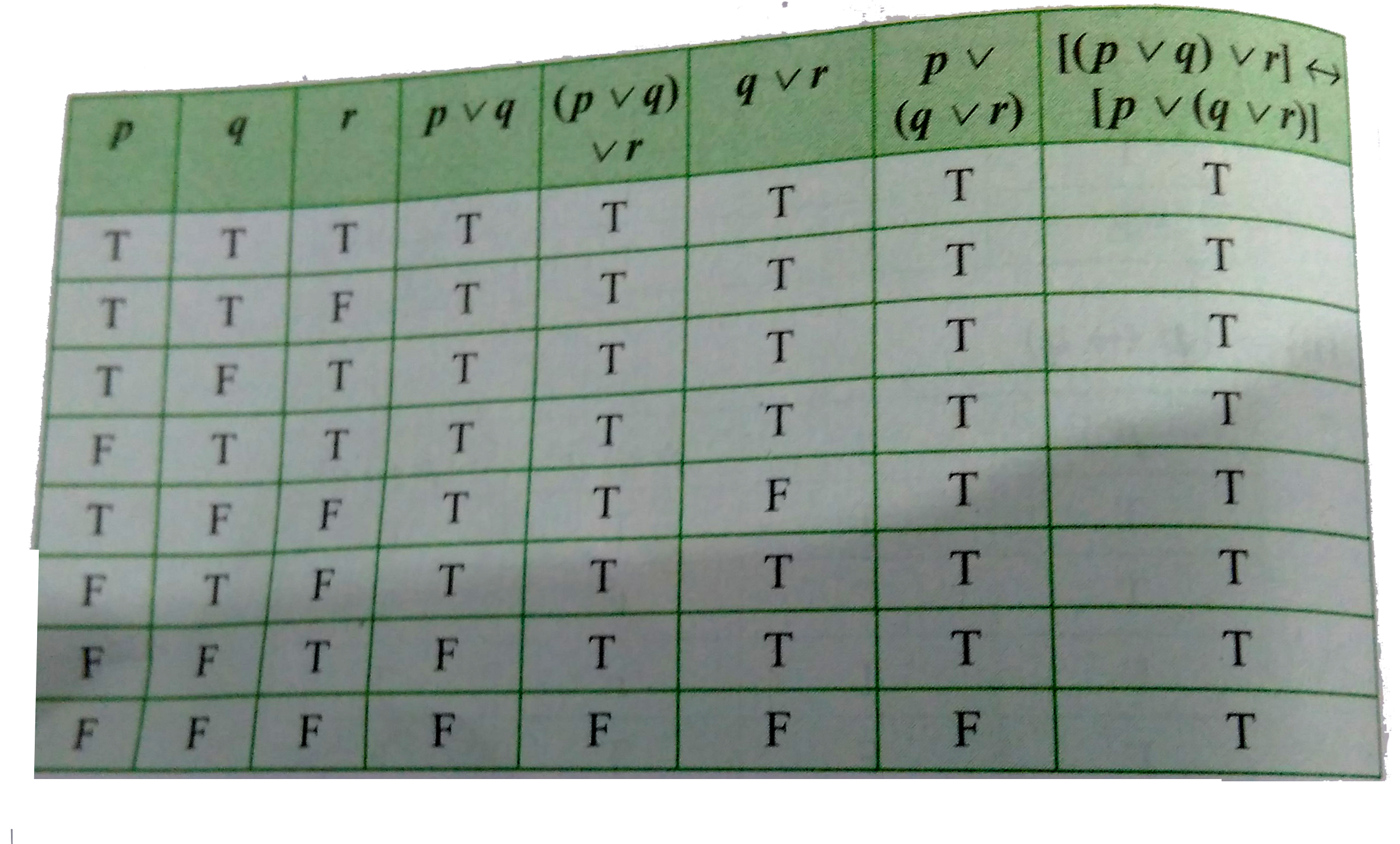
Thus, for all possible truth values of p,q and r , the compound statements : [p∨q)∨r]↔[p∨(q∨r)] is true.
∴[(p∨q)∨r]↔[p∨(q∨r)] is a tautology.
|
Topper's Solved these Questions
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.1
8 Videos
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.2
5 Videos
- LOGARITHM AND ITS PROPERTIESBOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year
5 Videos
- MATRICESBOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises
165 Videos
Similar Questions
Knowledge Check
Consider following statements Statement - I :
(p^~a)^(vpng) is a fallacy.
Statement - II : (p→q)↔(~q→~p) is a tautology.AStatement - I is true, statement -II is false.BStatement - I is false, Statement - II is true.CStatement - I true, Statement - II is true, Statement - II is a correct explanation for Statement - I.DStatement - I is true, Statement - II is true, Statement - II is not a correct explanation for Statement - I.Statement-1 : (p∧~q)∧(~p∧q) is a fallacy.
Statement -2: (p→q)↔(~q→~p) is a tautology .AStatement-1 is True, Statement -2 is Ture, Statement -2 is a correct explanation for statement -3BStatement-1 is True, Statement -2 is True,, Statement -2 is not a correct explanation for statement -3CStatement -1 is True , Statement -2 is false.DStatement -1 is False, statement -2 is True.
Show that
(i) p→(p∨q) is a tautology
(ii)(p∨q)∧(~p∧~q) is a contradiction
View SolutionShow that
(i) ~[p∧(~p)] is a tautology
(ii) ~[p∨(~p)] is a contradication.
View SolutionShow that (p∧q)∨(~p)∨(p∧~q) is a tautology
View Solution~(p∨(~p∨q)) is equal to
View SolutionWithout using truth table, prove that [(p∨q)∧~p]→q is a tautology.
View SolutionConsider : Statement I : (pˆ˜q)ˆ~pˆq is a fallacy. Statement II : (p→q)↔(~q→˜p) is a tautology. (1) Statement - I is True; Statement -II is true; Statement-II is not a correct explanation for Statement-I (2) Statement -I is True; Statement -II is False. (3) Statement -I is False; Statement -II is True (4) Statement -I is True; Statement -II is True; Statement-II is a correct explanation for Statement-I
View Solution