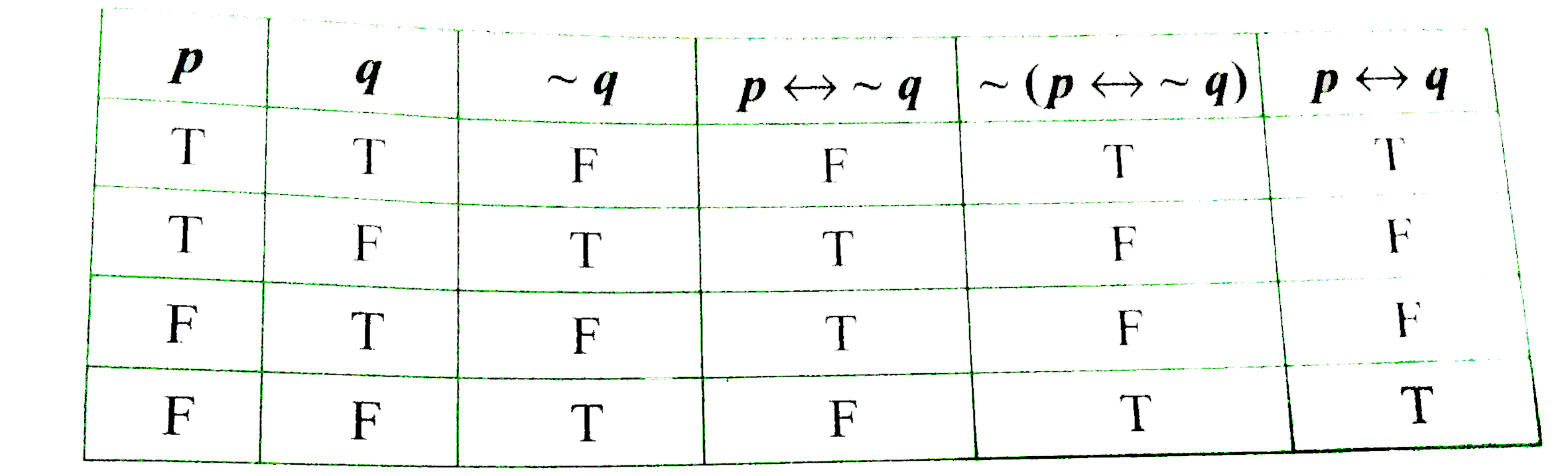
The statement ~(p↔~q) is
A
equivalent to p↔q
B
equivalent to ~p↔q
C
a tautology
D
a fallacy
Video Solution
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:Exercise (Single)
Explore 38 Videos
- LOGARITHM AND ITS PROPERTIESBook:CENGAGEChapter:LOGARITHM AND ITS PROPERTIESExercise:JEE Previous Year
Explore 5 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Solved Examples And Exercises
Explore 165 Videos
Similar Questions
Knowledge Check
The statement ~(p↔~q) is
Aequivalent to p↔qBequivalent to ~p↔qCa tautologyDa fallacyThe statement ~(p↔~q) is
Aequivalent to p↔qBequivalent to ~p↔qCtautologyDfallacyThe statement ~(p↔~q) is
Aequvalent to p↔qBequivalent to ~p↔qCa tautologyDa fallacy
The equivalent for of the statement ~(p→~q) is
View SolutionStatements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: (~p↔~q) is a tautology.
View SolutionThe statement (p⇒q)⇔(~p∧q) is a
View SolutionThe statement (p∧~q) is logically equivalent to-
View SolutionThe negation of the statement(~p∨~q) is
View Solution