The same colour of light takes t1 sec and t2 sec to travel the same distance ‘x’ in two media ‘A’ and ‘B’ respectively. Refractive index of medium ‘A’ w.r.t to ‘B’ is
xT1t2
t2xt1
t2t1
t1t2
The correct Answer is:D
To find the refractive index of medium A with respect to medium B, we can follow these steps:
1. Understanding the Problem: We know that light takes t1 seconds to travel a distance x in medium A and t2 seconds to travel the same distance x in medium B. We need to find the refractive index of medium A with respect to medium B.
2. Define the Speed of Light in Each Medium:
- The speed of light in a vacuum is denoted as c.
- The speed of light in medium A, denoted as vA, is given by:
\(
vA = \frac{c}{\mu_A}
\)
- The speed of light in medium B, denoted as vB, is given by:
\(
vB = \frac{c}{\mu_B}
\)
3. Using the Formula for Distance:
- The distance traveled in each medium can be expressed using the formula:
\(
x = v \cdot t
\)
- For medium A:
\(
x = vA \cdot t1 \implies x = \left(\frac{c}{\mu_A}\right) \cdot t1
\)
- For medium B:
\(
x = vB \cdot t2 \implies x = \left(\frac{c}{\mu_B}\right) \cdot t2
\)
4. Setting the Distances Equal:
- Since both expressions equal x, we can set them equal to each other:
\(
\frac{c}{\mu_A} \cdot t1 = \frac{c}{\mu_B} \cdot t2
\)
5. Canceling c from Both Sides:
- We can cancel c from both sides (assuming c is not zero):
\(
\frac{t1}{\mu_A} = \frac{t2}{\mu_B}
\)
6. Rearranging to Find the Refractive Index:
- Rearranging the equation gives us:
\(
\frac{\mu_A}{\mu_B} = \frac{t1}{t2}
\)
7. Conclusion:
- Therefore, the refractive index of medium A with respect to medium B is:
\(
\mu_A = \frac{t1}{t2} \cdot \mu_B
\)
Final Answer:
The refractive index of medium A with respect to medium B is:
\(
\mu_A = \frac{t1}{t2} \cdot \mu_B
\)
- The speed of light in a vacuum is denoted as c.
- The speed of light in medium A, denoted as vA, is given by:
\(
vA = \frac{c}{\mu_A}
\)
- The speed of light in medium B, denoted as vB, is given by:
\(
vB = \frac{c}{\mu_B}
\)
- The distance traveled in each medium can be expressed using the formula:
\(
x = v \cdot t
\)
- For medium A:
\(
x = vA \cdot t1 \implies x = \left(\frac{c}{\mu_A}\right) \cdot t1
\)
- For medium B:
\(
x = vB \cdot t2 \implies x = \left(\frac{c}{\mu_B}\right) \cdot t2
\)
- Since both expressions equal x, we can set them equal to each other:
\(
\frac{c}{\mu_A} \cdot t1 = \frac{c}{\mu_B} \cdot t2
\)
- We can cancel c from both sides (assuming c is not zero):
\(
\frac{t1}{\mu_A} = \frac{t2}{\mu_B}
\)
- Rearranging the equation gives us:
\(
\frac{\mu_A}{\mu_B} = \frac{t1}{t2}
\)
- Therefore, the refractive index of medium A with respect to medium B is:
\(
\mu_A = \frac{t1}{t2} \cdot \mu_B
\)
The refractive index of medium A with respect to medium B is:
\(
\mu_A = \frac{t1}{t2} \cdot \mu_B
\)
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)
5 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)
23 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFLECTION)
15 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
Knowledge Check
If a ray of light takes t1 and t2 times in two media of absolute refractive indices μ1 and μ2 respectively to travel same distance, then
Aμ1t1=μ2t2Bμ1t2=μ2t1Ct1√μ1=t2√μ2Dt1√μ2=t2√μ1Figure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is
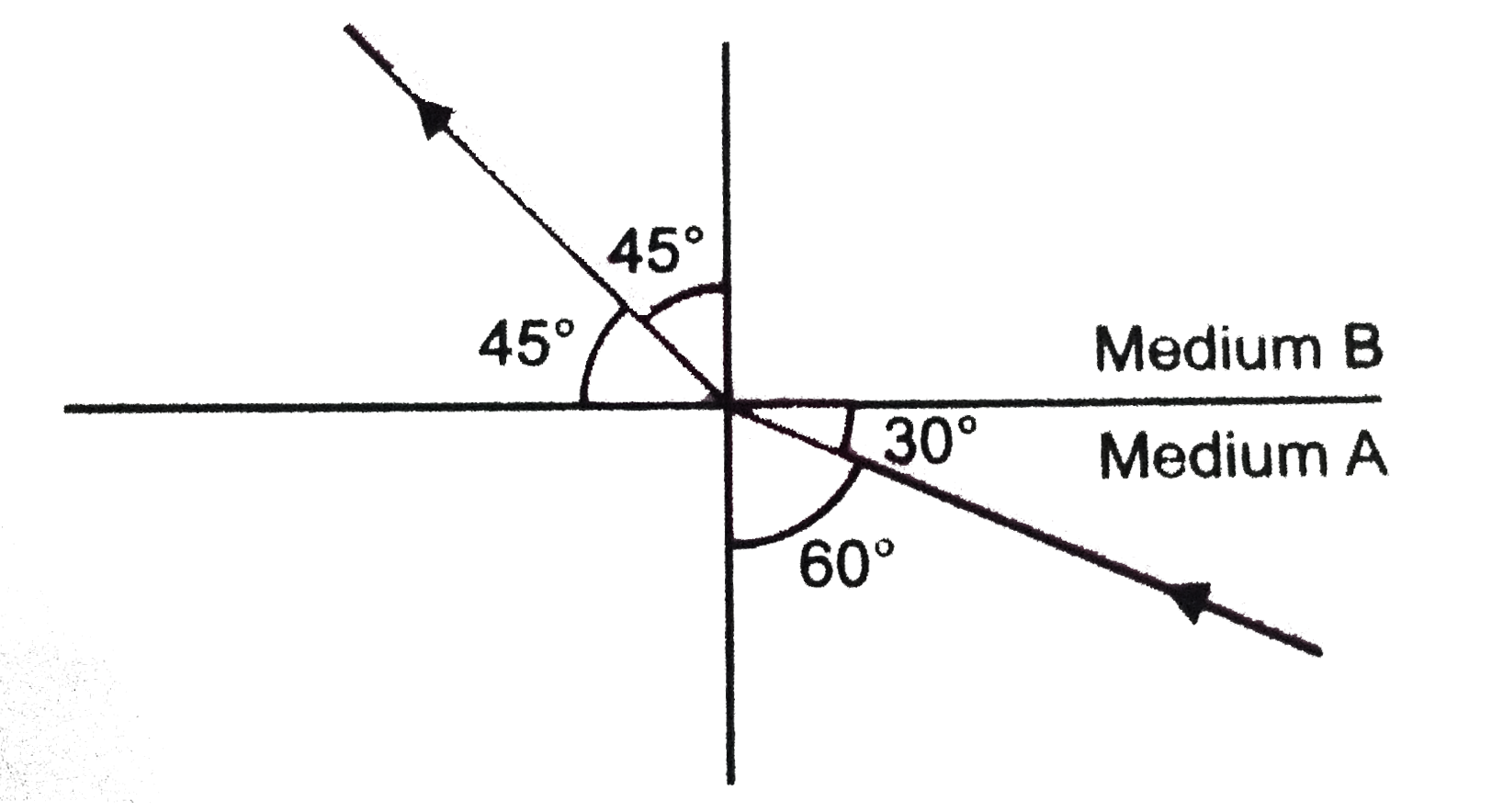 A√3/√2B√2/√3C1/√2D√2
A√3/√2B√2/√3C1/√2D√2Figure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is
 A√3√2B√2√3C1√2D√2
A√3√2B√2√3C1√2D√2
Velocity of light ray in two media A and Bare v1andv2 respectively.
What is the refractive index of B with respect to A?
View SolutionIf speed of light in a medium is 2×108m/sec. Find refractive index of medium.
View SolutionCan the relative refractive index of a medium w.r.t. another medium be less than unity ?
View SolutionFigure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is

View SolutionThe refractive indices of glass and water with respect to air are 3/2 and 4/3 respectively. The refractive index of glass w.r.t. water will be
View Solution
