A light ray is incident at an angle 45∘ on parallel sided glass slab and emerges out grazing the vertical surface. The refractive index of the slab is
√32
√52
√32
√52
The correct Answer is:A
To solve the problem of finding the refractive index of a parallel-sided glass slab through which a light ray grazes the vertical surface, we can follow these steps:
1. Understanding the Geometry:
- A light ray is incident at an angle of 45∘ on a parallel-sided glass slab.
- The ray emerges grazing the vertical surface, which means it exits the slab at an angle of 90∘ to the normal at the point of emergence.
2. Identify the Angles:
- Let θ1=45∘ (the angle of incidence).
- The angle of refraction θ2 when the light enters the slab can be found using Snell's Law:
n1sin(θ1)=n2sin(θ2)
- Here, n1=1 (the refractive index of air) and n2=μ (the refractive index of the glass slab).
3. Using Snell's Law:
- Substituting the known values into Snell's Law:
1⋅sin(45∘)=μ⋅sin(θ2)
- Since sin(45∘)=1√2, we have:
1√2=μ⋅sin(θ2)
4. Emergence Condition:
- When the ray emerges grazing the vertical surface, it means that the angle of incidence at the second surface is 90∘.
- Therefore, the angle of refraction at the second surface must be 0∘ (grazing condition).
5. Applying Snell's Law at Emergence:
- At the second surface, we apply Snell's Law again:
μ⋅sin(θ2)=1⋅sin(0∘)
- Since sin(0∘)=0, this condition indicates that the angle of incidence θ2 must be such that it leads to a critical angle condition.
6. Finding the Critical Angle:
- The critical angle θc can be defined as:
sin(θc)=1μ
- Since the ray grazes the vertical surface, we can set θ2=90∘−θc.
7. Relating Angles:
- From the geometry, we have:
θ2=45∘
- Therefore, we can set:
sin(45∘)=1μ
- This gives us:
1√2=1μ
8. Solving for the Refractive Index:
- Rearranging gives:
μ=√2
Final Answer:
The refractive index of the slab is μ=√2.
---
- A light ray is incident at an angle of 45∘ on a parallel-sided glass slab.
- The ray emerges grazing the vertical surface, which means it exits the slab at an angle of 90∘ to the normal at the point of emergence.
- Let θ1=45∘ (the angle of incidence).
- The angle of refraction θ2 when the light enters the slab can be found using Snell's Law:
n1sin(θ1)=n2sin(θ2)
- Here, n1=1 (the refractive index of air) and n2=μ (the refractive index of the glass slab).
- Substituting the known values into Snell's Law:
1⋅sin(45∘)=μ⋅sin(θ2)
- Since sin(45∘)=1√2, we have:
1√2=μ⋅sin(θ2)
- When the ray emerges grazing the vertical surface, it means that the angle of incidence at the second surface is 90∘.
- Therefore, the angle of refraction at the second surface must be 0∘ (grazing condition).
- At the second surface, we apply Snell's Law again:
μ⋅sin(θ2)=1⋅sin(0∘)
- Since sin(0∘)=0, this condition indicates that the angle of incidence θ2 must be such that it leads to a critical angle condition.
- The critical angle θc can be defined as:
sin(θc)=1μ
- Since the ray grazes the vertical surface, we can set θ2=90∘−θc.
- From the geometry, we have:
θ2=45∘
- Therefore, we can set:
sin(45∘)=1μ
- This gives us:
1√2=1μ
- Rearranging gives:
μ=√2
The refractive index of the slab is μ=√2.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFRACTION THROUGH SPHERICAL SURFACES )
Explore 29 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFRACTION THROUGH A PRISM )
Explore 8 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFLECTION)
Explore 18 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
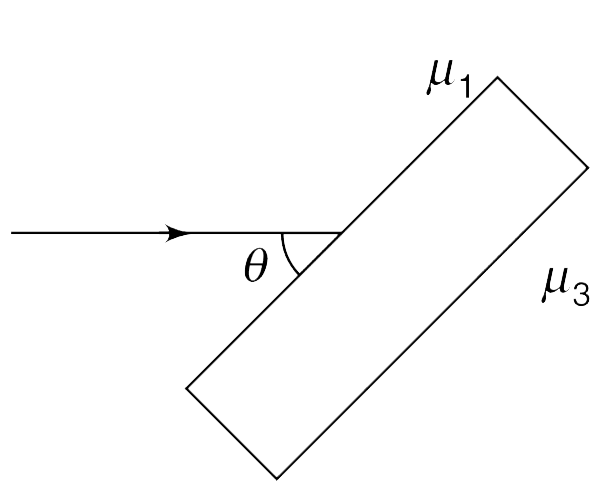
A light ray travelling in a medium of refractive index μ1 is incident on a parallel faced glass slab making an angle of θ with the glass surface. The refractive index of the medium on the other side of the glass slab is μ3(>μ1). Find the angular deviation suffered by the light ray.
View SolutionA ray of light is incident at an angle of 60° on a parallel side of a glass slab of thickness 0.1 m and refractive index 1.5. Calculate the lateral shift produced.
View Solution
Knowledge Check
A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3A ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
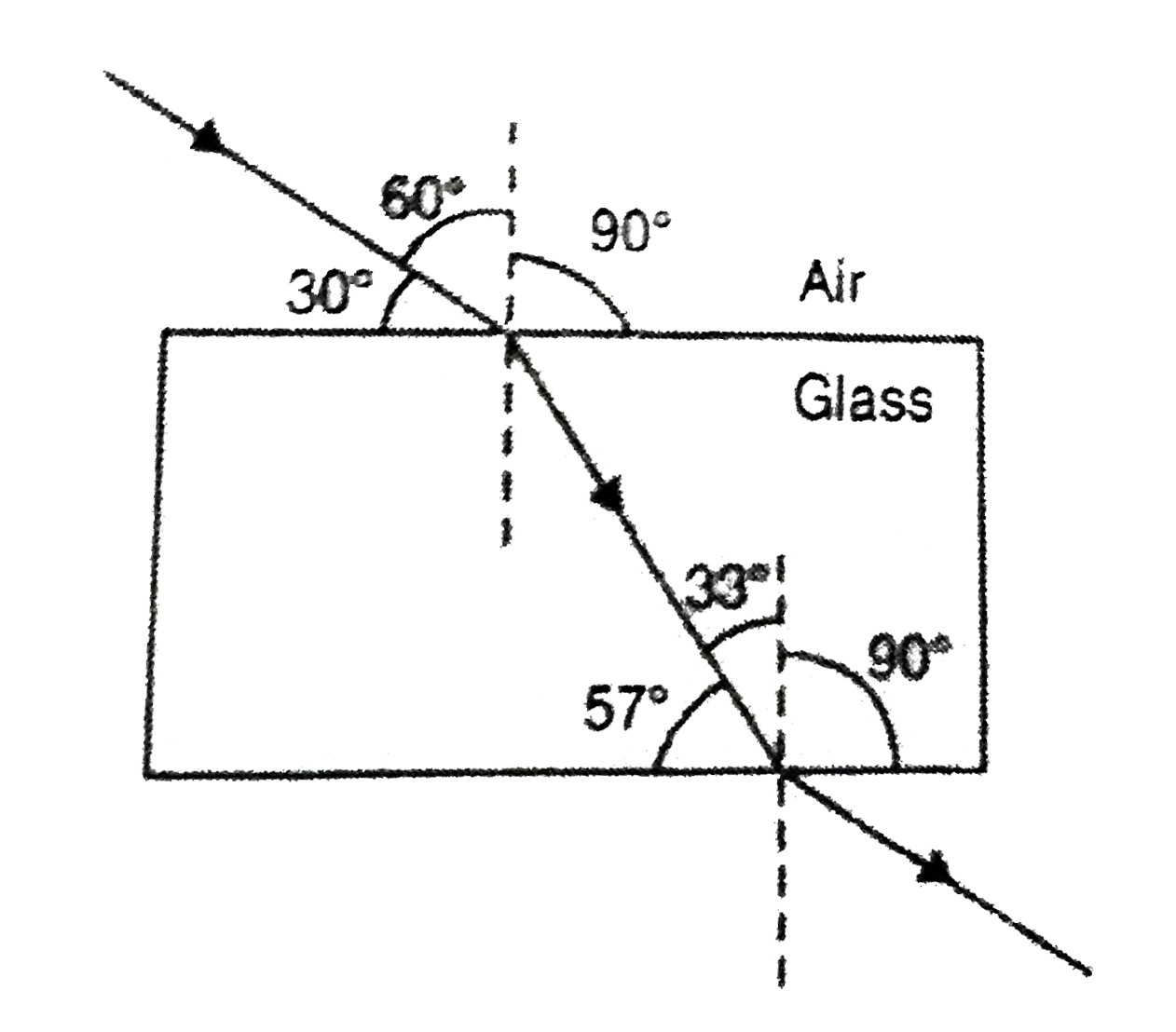 A60∘B33∘C57∘D30∘
A60∘B33∘C57∘D30∘Light is incident at an angle i on a glass slab. If the reflected ray is completely polarised , then the angle of refraction is
A180∘−iB90∘+iCiD90∘−i
A ray of light incident on the horizontal surface of a glass slab at 70∘ just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
View SolutionA light ray is incident at 45∘ on a glass slab. The slab is 3cm thick, and the refractive index of the glass is 1.5. What will the displacement of the ray be as a result of its passage through the slab? At what angle will the ray emerge formn the slab?
View SolutionIn an isosceles prism of prism angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergent ray grazes the emergent surface. Find the refractive index of the material of the prism.For what angle of incidence the angle of deviation will be minimum ?
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionLight is incident at an angle i on a glass slab. The reflected ray is completely polarished . The angle of refraction is
View Solution
