A ray of light incident on the horizontal surface of a glass slab at just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
To solve the problem, we need to find the critical angle and the refractive index of the glass slab given that a ray of light is incident at an angle of 70∘ and just grazes the adjacent vertical surface after refraction.
1. Understanding the Setup:
- We have a glass slab with a horizontal surface. A ray of light strikes this surface at an angle of 70∘ with respect to the normal.
- After refraction, the ray travels through the glass and just grazes the adjacent vertical surface, indicating that it is at the critical angle when it reaches the vertical surface.
2. Applying Snell's Law:
- According to Snell's Law, we have:
n1sin(θ1)=n2sin(θ2)
- Here, n1=1 (for air), θ1=70∘, and n2=μ (the refractive index of glass), and θ2=R (the angle of refraction).
3. Finding the Relationship Between Angles:
- Since the ray just grazes the vertical surface, it means that at this point, the angle of refraction R is equal to the critical angle C.
- Therefore, we can express R as:
R+C=90∘⇒R=90∘−C
4. Substituting into Snell's Law:
- We can rewrite Snell's Law using the relationship we found:
1⋅sin(70∘)=μ⋅sin(R)
- Substituting R=90∘−C:
sin(70∘)=μ⋅sin(90∘−C)=μ⋅cos(C)
5. Using the Critical Angle Formula:
- The critical angle C is related to the refractive index by:
sin(C)=1μ
- Rearranging gives:
μ=1sin(C)
6. Finding the Tangent of the Critical Angle:
- From the equation sin(70∘)=μ⋅cos(C), we can substitute μ:
sin(70∘)=cos(C)sin(C)
- This can be rewritten as:
tan(C)=1sin(70∘)
7. Calculating the Critical Angle:
- To find C, we take the inverse tangent:
C=tan−1(1sin(70∘))
- Calculating this gives C≈46∘.
8. Finding the Refractive Index:
- Now substituting C back into the refractive index formula:
μ=1sin(46∘)≈1.37
Final Answers:
- Critical Angle C: 46∘
- Refractive Index of Glass μ: 1.37
- We have a glass slab with a horizontal surface. A ray of light strikes this surface at an angle of 70∘ with respect to the normal.
- After refraction, the ray travels through the glass and just grazes the adjacent vertical surface, indicating that it is at the critical angle when it reaches the vertical surface.
- According to Snell's Law, we have:
n1sin(θ1)=n2sin(θ2)
- Here, n1=1 (for air), θ1=70∘, and n2=μ (the refractive index of glass), and θ2=R (the angle of refraction).
- Since the ray just grazes the vertical surface, it means that at this point, the angle of refraction R is equal to the critical angle C.
- Therefore, we can express R as:
R+C=90∘⇒R=90∘−C
- We can rewrite Snell's Law using the relationship we found:
1⋅sin(70∘)=μ⋅sin(R)
- Substituting R=90∘−C:
sin(70∘)=μ⋅sin(90∘−C)=μ⋅cos(C)
- The critical angle C is related to the refractive index by:
sin(C)=1μ
- Rearranging gives:
μ=1sin(C)
- From the equation sin(70∘)=μ⋅cos(C), we can substitute μ:
sin(70∘)=cos(C)sin(C)
- This can be rewritten as:
tan(C)=1sin(70∘)
- To find C, we take the inverse tangent:
C=tan−1(1sin(70∘))
- Calculating this gives C≈46∘.
- Now substituting C back into the refractive index formula:
μ=1sin(46∘)≈1.37
- Critical Angle C: 46∘
- Refractive Index of Glass μ: 1.37
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Sample Problem(a)
Explore 5 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(a)
Explore 14 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(NCERT)Exercise With Solution
Explore 38 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
A ray of light incident on the horizontal surface of a glass slab at an angle of incidence ‘i’just grazes the adjacent vertical surface after reflection. Compute the critical angle and refractive index of glass
View SolutionConsider the figure given below. A ray of light is incident on one of the horizontal surfaces of glass slab at an angle of 60∘ and it just grazes along the adjacent vertical sides after refraction. Calculate the critical angle .
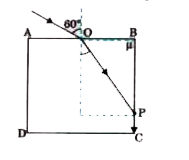
View Solution
Knowledge Check
A light ray is incident at an angle 45∘ on parallel sided glass slab and emerges out grazing the vertical surface. The refractive index of the slab is
A√32B√52C√32D√52A ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
A33.7∘B23.7∘C43.7∘D53.7∘A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
A35∘B39∘C42∘D44∘
A ray of light is incident on the surface of a glass plate of index of refraction 1.55 at the polarizing angle. Calculate the angle of refraction.
View SolutionAt the bottom of a trough filled with water a rectangular glass slab is placed. A ray of light is incident on the water surface at an angle of 30∘ and enters the glass after passing through the water. What is the angle of refraction in glass? Given, refractive index of water is 1.33 and that of glass is 1.5.
View SolutionA ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
View SolutionA ray of light is incident normally on one of the refracting surfaces of a prism of refracting angle A,. The emergent ray grazes the other refracting surface. Find the refractive index of the material ofprism.
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View Solution