An under water swimmer looks upward at an unobstructed overcast sky. The vertex angle does the sky appear to subtend at the eye of swimmer is (critical angle for water air interface is C)
C
C/2
2C
3C
The correct Answer is:C
To solve the problem of determining the vertex angle that the sky appears to subtend at the eye of an underwater swimmer, we can follow these steps:
1. Understanding the Setup:
- The swimmer is underwater, looking up towards the sky.
- We need to consider the critical angle (C) for the water-air interface, which is the angle of incidence above which total internal reflection occurs.
2. Identifying the Critical Ray:
- When the swimmer looks up, light rays from the sky enter the water.
- The critical ray is the ray that makes an angle of C with the normal at the water-air interface. Beyond this angle, light will not exit the water but will be totally internally reflected.
3. Drawing the Diagram:
- Imagine a vertical line representing the water surface.
- Draw the normal line (perpendicular) to the surface at the point where the swimmer is looking up.
- The critical angle (C) is measured from the normal to the critical ray.
4. Calculating the Vertex Angle:
- The critical ray makes an angle C with the normal on both sides (left and right) of the vertical line.
- Therefore, the angle between the two critical rays (the vertex angle θ) is given by:
θ=C+C=2C
5. Conclusion:
- The vertex angle that the sky appears to subtend at the eye of the swimmer is 2C.
Final Answer:
The vertex angle that the sky appears to subtend at the eye of the swimmer is 2C.
---
- The swimmer is underwater, looking up towards the sky.
- We need to consider the critical angle (C) for the water-air interface, which is the angle of incidence above which total internal reflection occurs.
- When the swimmer looks up, light rays from the sky enter the water.
- The critical ray is the ray that makes an angle of C with the normal at the water-air interface. Beyond this angle, light will not exit the water but will be totally internally reflected.
- Imagine a vertical line representing the water surface.
- Draw the normal line (perpendicular) to the surface at the point where the swimmer is looking up.
- The critical angle (C) is measured from the normal to the critical ray.
- The critical ray makes an angle C with the normal on both sides (left and right) of the vertical line.
- Therefore, the angle between the two critical rays (the vertex angle θ) is given by:
θ=C+C=2C
- The vertex angle that the sky appears to subtend at the eye of the swimmer is 2C.
The vertex angle that the sky appears to subtend at the eye of the swimmer is 2C.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFRACTION THROUGH SPHERICAL SURFACES )
Explore 29 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFRACTION THROUGH A PRISM )
Explore 8 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFLECTION)
Explore 18 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
A fish in a water tank sees the outside world as if it (the fish) is at the vertex of cone such that the circular base of the cone coincides with the surface of water. Given the depth of water where fish is located being h and the critical angle for water - air interface being iC, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height h.
View SolutionA fish in a water tank sees the outside world as if it (the fish) is at the vertex of cone such that the circular base of the cone coincides with the surface of water. Given the depth of water where fish is located being h and the critical angle for water-air interface being ic, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height h.
View Solution
Knowledge Check
A fish looks upward at an unobstructed overcast sky. What total angle does the sky appear to subten?(Take refractive index of water as √2.)
A180∘B90∘C75∘D60∘A diver at a depth of 12 m in water (μ=4/3) sees the sky in a cone of semi-vertical angle
Asin−1(4/3)Btan−1(4/3)Csin−1(3/4)D90∘When the surface of a lake is calm , a fish submerged in water will see the entire outside world within an inverted cone whose vertex is situated at the eye of the fish . What is the vertex angle of the cone ?
(anw=43) and sin49∘=0.75A110∘B98∘C48∘D68∘
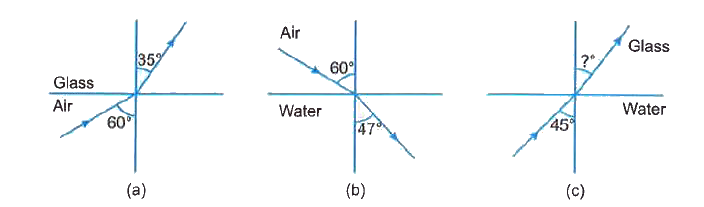
Fig. 9.02(a) and (b), show refraction of a ray in air incident at 60∘ with the normal to a glass - air and water - air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45∘ with the normal to a water - glass interface [Fig. 9.02(c)].
View Solutiona) The anlge subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnifications?
b) in viewing through a magnifying glass, one usually positions one's eyes very close to the lens. Does angular magnification change if the eye is moved back?
c) magnifying power of a simple microscopes is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?
d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?
e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it fot best veiwing. Why? How much should be that short distance between the eye and eyepiece?
View SolutionAnswer the following questions :
(a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification ?
(b) In viewing through a magnifying glass, one usually positions one's eyes very close to the lens. Does angular magnification change if the eye is moved back ?
(c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power ?
(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths ?
(e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why ? How much should be that short distance between the eye and eyepiece ?
View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View SolutionAn air masked eye placed inside water refractive index, μ sees the outside world. The vertex angle of the cone in which the eye will see the outside world is
View Solution

