Equal charges q are placed at the three corners B, C, D of a square ABCD of side 'a'. The ratio of potential at A to centre O is
2√2+13√2
2+√26
2√2+16
2√2+13
The correct Answer is:C
To solve the problem of finding the ratio of the electric potential at point A to that at the center O of the square ABCD, we will follow these steps:
Step 1: Calculate the potential at point A
The electric potential V due to a point charge q at a distance r is given by the formula:
V=k⋅qr
where k is Coulomb's constant, approximately 8.99×109N m2/C2.
In our case, we have three charges q located at points B, C, and D. We need to find the distance from point A to each of these charges:
1. Distance from A to B: AB=a
2. Distance from A to C: AC=√a2+a2=a√2
3. Distance from A to D: AD=a
Now, we can calculate the total potential at point A due to the three charges:
VA=VB+VC+VD
Substituting the distances into the potential formula:
VA=k⋅qa+k⋅qa√2+k⋅qa
Combining the terms:
VA=k⋅qa+k⋅qa+k⋅qa√2=2kqa+kqa√2
Step 2: Calculate the potential at the center O
The center O of the square is at a distance of a√2 from each of the corners B, C, and D. Therefore, the potential at point O due to each charge is:
VO=VB+VC+VD
Calculating the potential at O:
VO=k⋅qa√2+k⋅qa√2+k⋅qa√2
This simplifies to:
VO=3⋅k⋅q⋅√2a
Step 3: Find the ratio of potentials VAVO
Now we can find the ratio of the potentials at A and O:
VAVO=(2kqa+kqa√2)3⋅kq⋅√2a
Canceling kq/a:
VAVO=2+1√23√2
Step 4: Simplify the ratio
To simplify further, we can express 1√2 as √22:
VAVO=2+√223√2=4+√26√2
Thus, the final ratio of the potential at A to that at O is:
VAVO=4+√26√2
2. Distance from A to C: AC=√a2+a2=a√2
3. Distance from A to D: AD=a
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 4 (NCERT EXAMPLAR PROBLEMS)
Explore 6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise-2(C.W)
Explore 53 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
Four charges +q,+2q,+3q and +4q are placed at the four corners ABCD of a square of side a. Calculate the field and potential at the centre of the square.
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View Solution
Knowledge Check
Equal charges q are placed at the three corners B, C, D of a square ABCD of side a. The potential at A is
A14πε0qaB3q4πε0Cq4πε0a[2+1√2]Dq4πε0a[1+√2]Equal charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
A3Q24πε0a2B4Q24πε0a2C(1+1√22)Q24πε0a2D(2+1√2)Q24πε0a2Three charges ,each of +4μC ,are placed at the corners A,B,C of a square ABCD of side 1m.The electric field at the centre O of a square ABCD of side 1m.The electric field at the centre O of the square is
A7.2×104N/C towards DB7.2×104N/C towards BC3.6×104N/C towards AD7.2×104N/C towards C
Five equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionFour point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
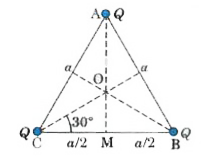
View SolutionThree identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
View SolutionEqual charges q are placed at the four corners A,B,C,Dof a square of length a. The magnitude of the force on the charge at B will be
View SolutionThree masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View Solution
