Three identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
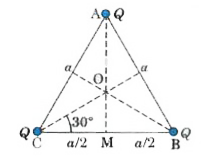
cos30∘=MCOC=a2OC
⇒OC=a22√3=a√3=OA=OB
The potential at O is same for all charges, so we can multiply the potential due to any of the charges by three to get the net potential at point O. Hence, potential at point O is as follows:
VO=314πε0QOC=3Q4πε0(a√3)
⇒VO=3√3Q4πε0a
At point M, the potential due to B and C are same, and the potential due to charge on A has different magnitude. Hence, the total potential at M is as follows:
VM=214πε0QBM+14πε0QAM
⇒VM=214πε0Qa2+14πε0Q√a2−a24
⇒VM=14πε04Qa+14πε02Qa√3
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 1
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 2
Explore 21 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
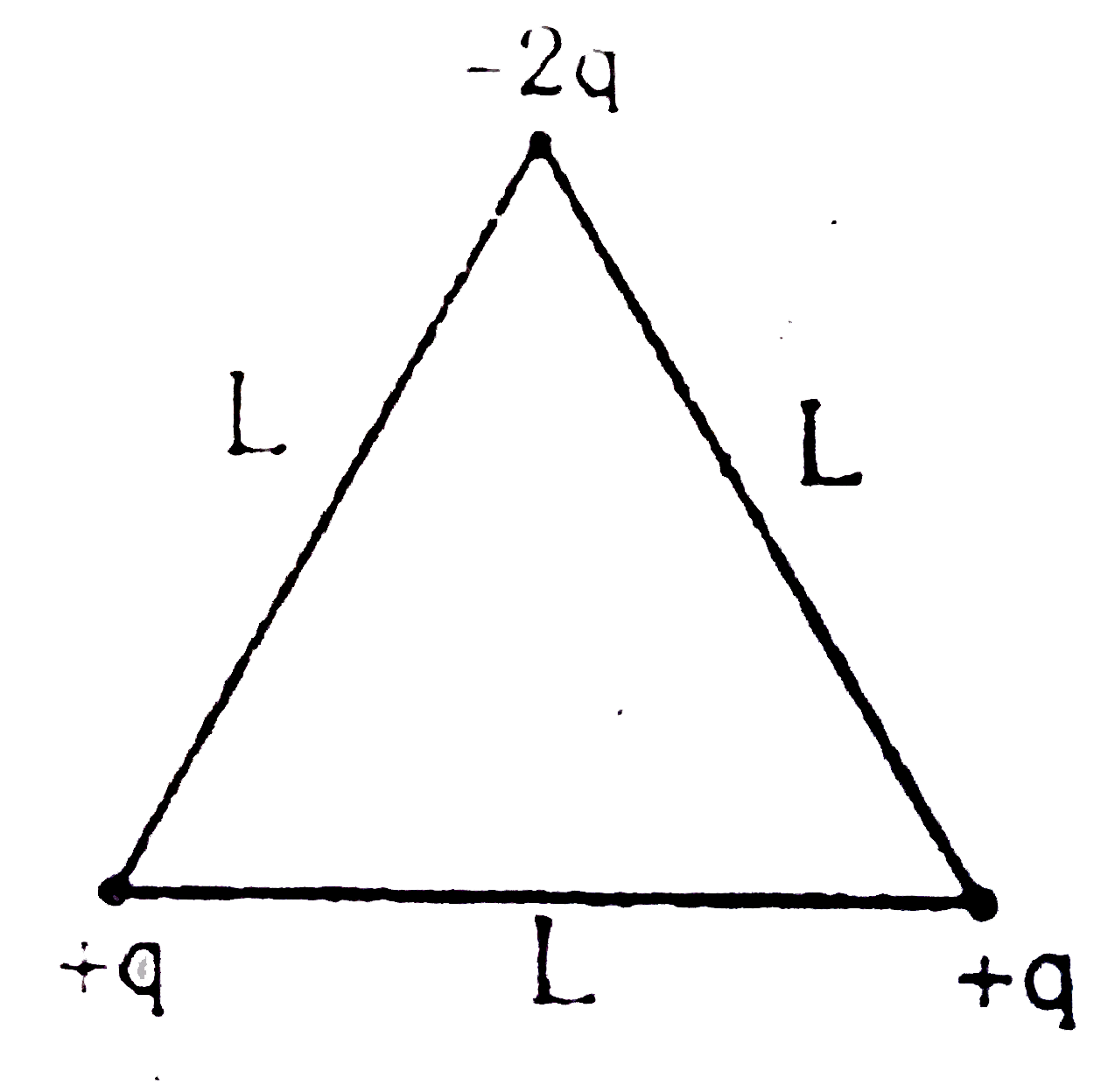
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
View SolutionThree point charges are kept at the three corners of an equilateral triangle of edge length a, as shown in the figure. The net electric dipole moment of the system is

View Solution
Knowledge Check
Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2Three equal charges Q are placed at the three corners of an equilateral triangle of side length a. Work done in shifting a charge q from infinity to the centroid of the triangle is
A3Qq4π∈0aB3Qq4π∈0√3aC3√3Qq4π∈0aD√3Qq4π∈03aThree charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
A18×10−6JB9JC9×10−6JD27J
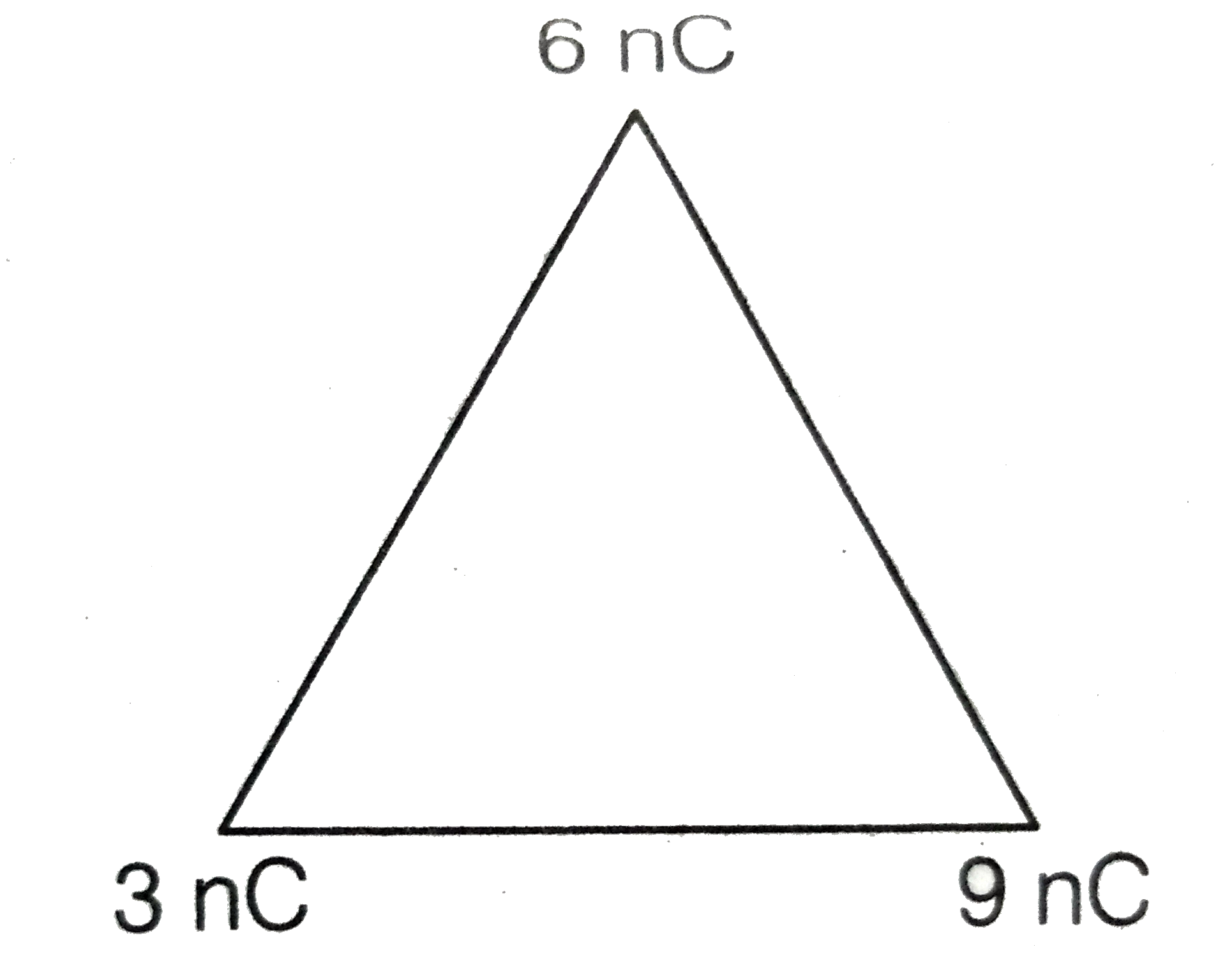
Three point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
View SolutionEqual charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View SolutionThree charges of 1 nC, 2 nC and 3 nC are placed at the corners of an equilateral triangle of side √3m. Calculate electrostatic potential at a point equidistant from the three corners of the triangle.
View SolutionThree point charges are placed at the corner of an equilateral triangle. Assuming only electrostatic forces are acting.
View Solution

