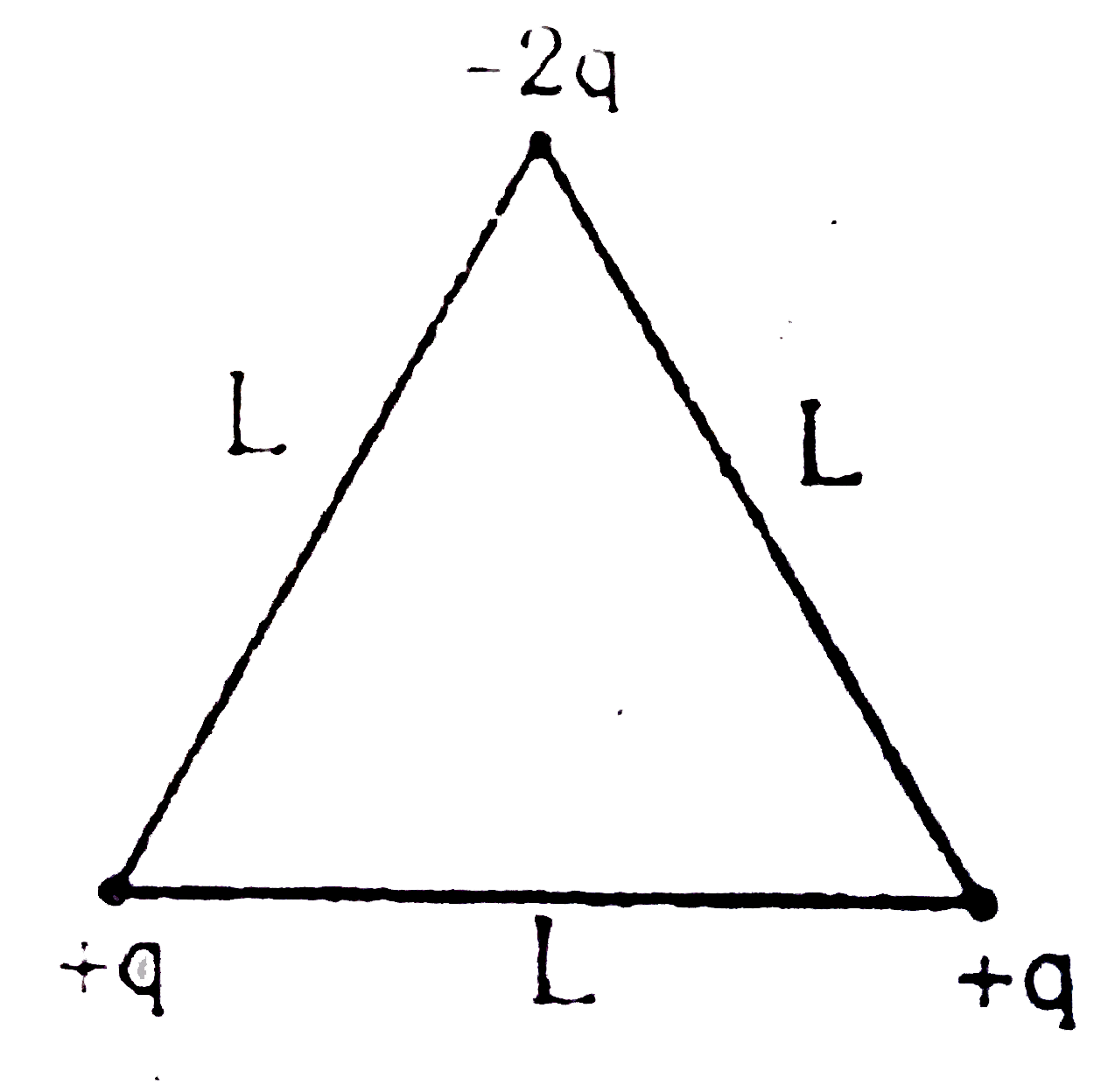
Three point charges are placed at the corner of an equilateral triangle. Assuming only electrostatic forces are acting.
the system can never be in equilibrium
the system will be equilibrium if the charges rotate about the centre of the triangle
the system will be in equilibrium if the charges have different magnitudes and different signs
the system will be in equilibrium if the charges have the same magnitude but different signs.
The correct Answer is:A
To solve the problem of determining the conditions under which three point charges placed at the corners of an equilateral triangle can be in equilibrium, we can follow these steps:
Step 1: Understand the Forces Acting on Each Charge
In an equilateral triangle, each charge will experience forces due to the other two charges. If we label the charges as q1, q2, and q3, we need to analyze the forces acting on each charge.
Step 2: Analyze the Forces on One Charge
Let's consider the charge q1. The forces acting on q1 due to q2 and q3 will depend on the nature of the charges (whether they are like or unlike).
- If q2 and q3 are of the same sign as q1, then q1 will experience repulsive forces from both q2 and q3.
- If q2 and q3 are of opposite sign to q1, then q1 will experience attractive forces from both.
Step 3: Conditions for Equilibrium
For q1 to be in equilibrium, the net force acting on it must be zero. This can happen if:
1. The magnitudes of the forces acting on q1 from q2 and q3 are equal.
2. The directions of these forces must be opposite.
Step 4: Analyze the Geometry
In an equilateral triangle, the angles between the lines connecting the charges are 60∘. Therefore, the forces due to q2 and q3 acting on q1 cannot be directly opposite to each other. This means that even if the magnitudes of the forces are equal, they cannot cancel each other out due to their directions.
Step 5: Conclusion
Since the forces cannot be equal and opposite due to the geometry of the triangle, we conclude that it is impossible for the system to be in equilibrium under the influence of electrostatic forces alone.
Final Answer
The system of three point charges placed at the corners of an equilateral triangle can never be in equilibrium.
---
In an equilateral triangle, each charge will experience forces due to the other two charges. If we label the charges as q1, q2, and q3, we need to analyze the forces acting on each charge.
Let's consider the charge q1. The forces acting on q1 due to q2 and q3 will depend on the nature of the charges (whether they are like or unlike).
- If q2 and q3 are of opposite sign to q1, then q1 will experience attractive forces from both.
For q1 to be in equilibrium, the net force acting on it must be zero. This can happen if:
1. The magnitudes of the forces acting on q1 from q2 and q3 are equal.
2. The directions of these forces must be opposite.
In an equilateral triangle, the angles between the lines connecting the charges are 60∘. Therefore, the forces due to q2 and q3 acting on q1 cannot be directly opposite to each other. This means that even if the magnitudes of the forces are equal, they cannot cancel each other out due to their directions.
Since the forces cannot be equal and opposite due to the geometry of the triangle, we conclude that it is impossible for the system to be in equilibrium under the influence of electrostatic forces alone.
The system of three point charges placed at the corners of an equilateral triangle can never be in equilibrium.
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field Due To Point Charge
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion
37 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
Three charges each of magnitude q are placed at the corners of an equilateral triangle, the electrostatic force on the charge place at the centre is (each side of triangle is L)
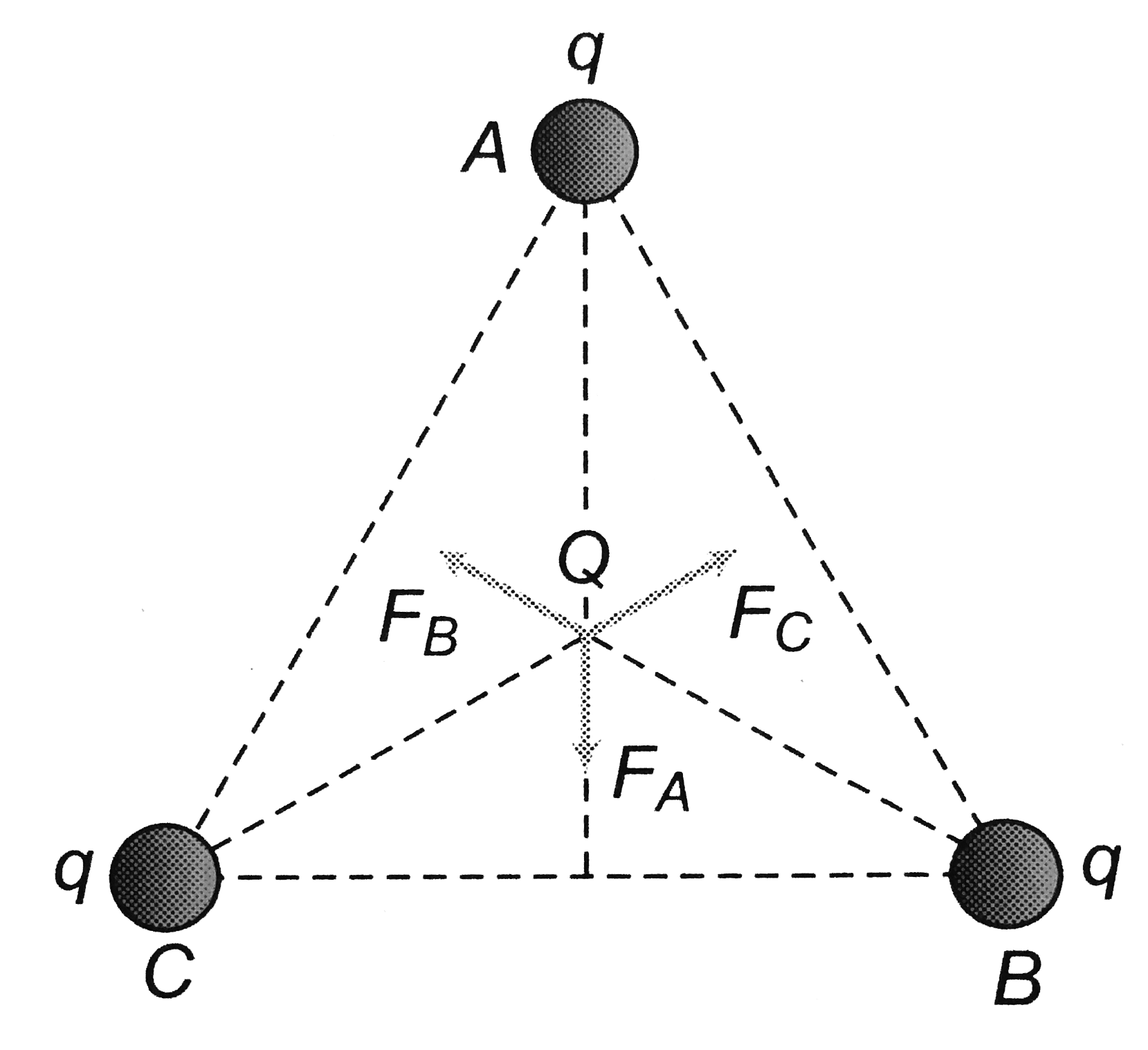 AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2
AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2Three charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
A3q24πε0a2Bq24πε0a2Cq22πε0a2D3q22πε0a2
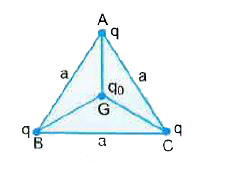
Three identical charges of q each are placed at the three verticess of an equilateral triangle ABC of side a, Electrostatic force experienced by a point charge q0 situated at the centroid G of triangle is ___________
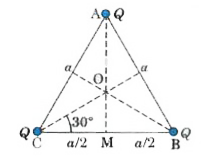
View SolutionThree identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
View SolutionThree point charges of 1C, 2C and 3C are placed at the . corners of an equilateral triangle of side 1m. Calculate the work required to move these charges to the corners of a smaller equilateral triangle of side 1.5m.
View Solution(i) Three equak charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out dorce acting on one of the charge due to other two charges ?
(ii) In the above question, if one of the charge is replaced by negative charge then find out force acting on it due to other charges ?
(iii) Repeat the part (i) if magnitude of each charge is doubled and side of triangle is reduced to half.
View SolutionThree identical point charges, q, are placed at the vertices of an equilateral triangle as shown in the figure. The length of each side of the triangle is d. Determine the magnitude and direction of the total electrostatic force on the charge at the top of the triangle.
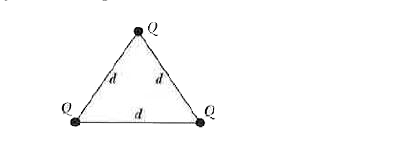
View Solution