Four particles, each of mass m and charge q, are held at the vertices of a square of side 'a'. They are released at t = 0 and move under mutual repulsive forces speed of any particle when its distance from the centre of square doubles is
[14π∈0q2ma(1+12√2)]12
(14π∈0q2ma)12
[14π∈02q2ma2(1+12√2)]12
(14π∈0q2ma2)12
The correct Answer is:A
To solve the problem of finding the speed of any particle when its distance from the center of the square doubles, we can follow these steps:
Step 1: Understand the Initial Configuration
We have four particles, each with mass m and charge q, positioned at the vertices of a square with side length a. The distance from the center of the square to any vertex is given by:
d=a√2
Step 2: Determine the Initial Potential Energy
The potential energy U between two charges q separated by a distance r is given by:
U=kq2r
where k is Coulomb's constant.
For our square configuration:
- There are 4 pairs of charges on the sides, each at a distance a.
- There are 2 pairs of charges on the diagonals, each at a distance √2a.
Thus, the initial potential energy Ui is:
Ui=4(kq2a)+2(kq2√2a)=4kq2a+2kq2√2a
Step 3: Determine the Final Configuration
When the particles move away from each other, the distance from the center of the square doubles. The new distance from the center to any vertex becomes:
d′=2d=2⋅a√2=√2a
Step 4: Calculate the Final Potential Energy
Now, we need to calculate the final potential energy Uf when the particles are at this new distance:
- The distance between charges on the sides is now 2a.
- The distance between charges on the diagonals is now 2√2a.
Thus, the final potential energy Uf is:
Uf=4(kq22a)+2(kq22√2a)=2kq2a+kq2√2a
Step 5: Calculate the Change in Potential Energy
The change in potential energy ΔU is given by:
ΔU=Uf−Ui
Substituting the expressions for Uf and Ui:
ΔU=(2kq2a+kq2√2a)−(4kq2a+2kq2√2a)
=−2kq2a−kq2√2a
Step 6: Relate Change in Potential Energy to Kinetic Energy
According to the work-energy theorem, the change in kinetic energy ΔK is equal to the negative of the change in potential energy:
ΔK=−ΔU
The initial kinetic energy is zero (since they start from rest), so:
12mv2=−ΔU
Step 7: Solve for Speed
Substituting ΔU into the equation:
12mv2=2kq2a+kq2√2a
v2=4kq2ma+2kq2√2ma
v=√4kq2ma+2kq2√2ma
Final Result
Thus, the speed of any particle when its distance from the center of the square doubles is:
v=
⎷kq2ma(4+2√2)
We have four particles, each with mass m and charge q, positioned at the vertices of a square with side length a. The distance from the center of the square to any vertex is given by:
d=a√2
The potential energy U between two charges q separated by a distance r is given by:
U=kq2r
where k is Coulomb's constant.
- There are 4 pairs of charges on the sides, each at a distance a.
- There are 2 pairs of charges on the diagonals, each at a distance √2a.
Ui=4(kq2a)+2(kq2√2a)=4kq2a+2kq2√2a
When the particles move away from each other, the distance from the center of the square doubles. The new distance from the center to any vertex becomes:
d′=2d=2⋅a√2=√2a
Now, we need to calculate the final potential energy Uf when the particles are at this new distance:
- The distance between charges on the sides is now 2a.
- The distance between charges on the diagonals is now 2√2a.
Uf=4(kq22a)+2(kq22√2a)=2kq2a+kq2√2a
The change in potential energy ΔU is given by:
ΔU=Uf−Ui
ΔU=(2kq2a+kq2√2a)−(4kq2a+2kq2√2a)
=−2kq2a−kq2√2a
According to the work-energy theorem, the change in kinetic energy ΔK is equal to the negative of the change in potential energy:
ΔK=−ΔU
The initial kinetic energy is zero (since they start from rest), so:
12mv2=−ΔU
Substituting ΔU into the equation:
12mv2=2kq2a+kq2√2a
v2=4kq2ma+2kq2√2ma
v=√4kq2ma+2kq2√2ma
Thus, the speed of any particle when its distance from the center of the square doubles is:
v=
⎷kq2ma(4+2√2)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 4 (NCERT EXAMPLAR PROBLEMS)
Explore 6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise-2(C.W)
Explore 53 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2GmlFind the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
A+4.0GB7.5GC−5.4GD+6.3GFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
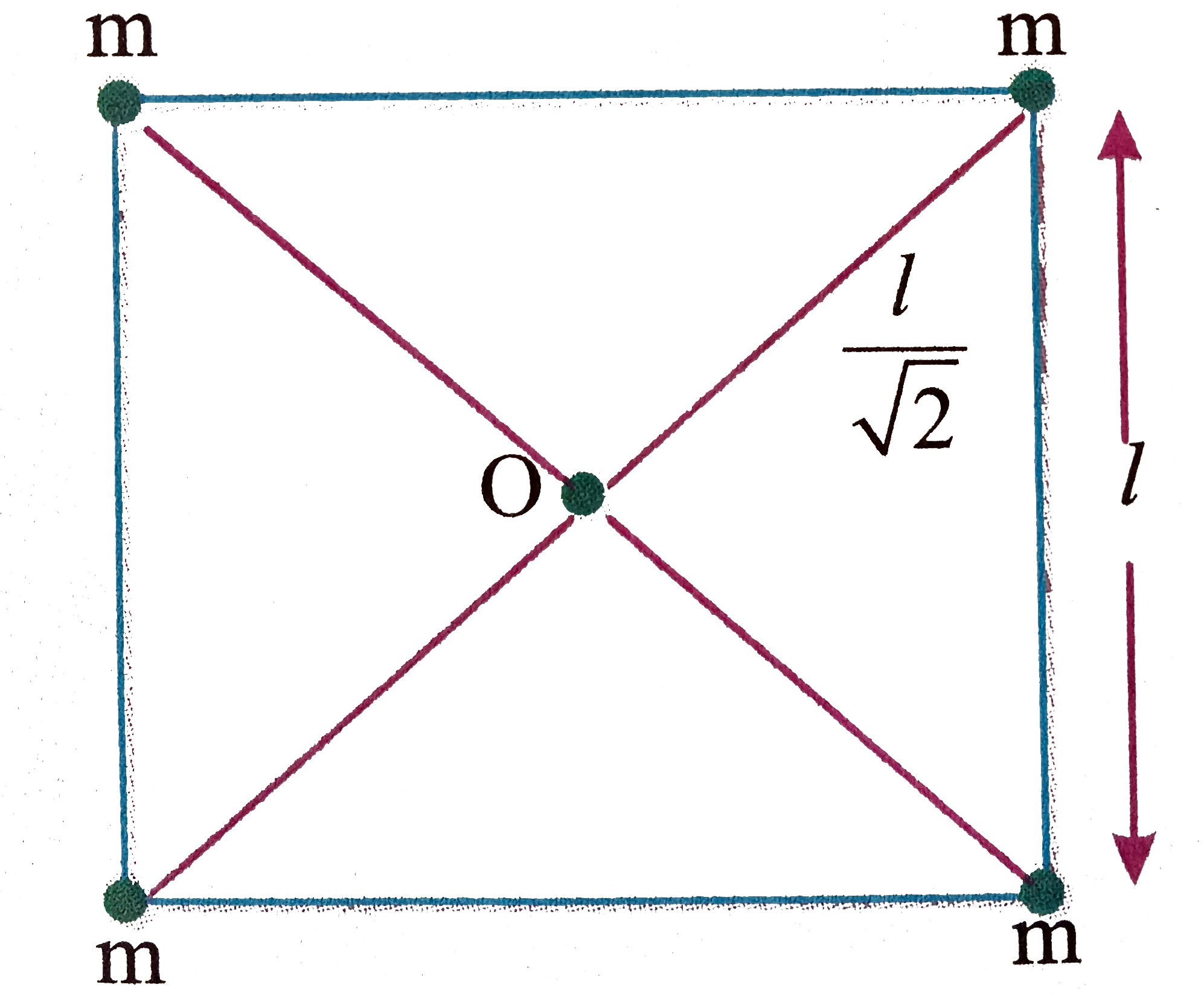 A−√32GMLB−√64GML2CzeroD−√16GML
A−√32GMLB−√64GML2CzeroD−√16GML
Four particle each of mass 1kg are at the four orners of a square of side 1m . The work done to move one of the particles to infinity
View SolutionFour particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionA, B, C and D are four particles with each of mass M lying on the vertices of a square of side a. They always move along a common circle with velocity v under mutual gravitational force. Find v so that they always remain on the vertices of the square
View Solution

