A and B are two condensers of capacities 2μF and 4μF. They are charged to potential differences of 12V and 6V respectively. If they are now connected (+ve to +ve), the charge that flows through the connecting wire is
24μC from A to B
8μC from A to B
8μC from B to A
24μC from B to A
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the initial charges on each capacitor.
The charge Q on a capacitor is given by the formula:
Q=C×V
where C is the capacitance and V is the voltage.
1. For capacitor A:
- Capacitance C1=2μF=2×10−6F
- Voltage V1=12V
- Charge Q1=C1×V1=2×10−6×12=24μC
2. For capacitor B:
- Capacitance C2=4μF=4×10−6F
- Voltage V2=6V
- Charge Q2=C2×V2=4×10−6×6=24μC
Step 2: Determine the total charge before connecting the capacitors.
The total charge Qtotal before connecting the capacitors is:
Qtotal=Q1+Q2=24μC+24μC=48μC
Step 3: Connect the capacitors (positive to positive).
When capacitors are connected positive to positive, they share the total charge until they reach a common potential. The total capacitance Cnet of capacitors in parallel is given by:
Cnet=C1+C2=2μF+4μF=6μF
Step 4: Calculate the common potential after connection.
The common potential Vcommon can be calculated using the formula:
Vcommon=QtotalCnet
Substituting the values:
Vcommon=48μC6μF=8V
Step 5: Calculate the final charges on each capacitor.
Now that we have the common potential, we can find the final charges on each capacitor using the formula Q=C×V.
1. For capacitor A:
- QA=C1×Vcommon=2μF×8V=16μC
2. For capacitor B:
- QB=C2×Vcommon=4μF×8V=32μC
Step 6: Calculate the charge that flows through the connecting wire.
The charge that flows through the connecting wire is the difference between the initial charge and the final charge on each capacitor.
1. For capacitor A:
- Initial charge Q1=24μC
- Final charge QA=16μC
- Charge that flows from A: QflowA=Q1−QA=24μC−16μC=8μC
2. For capacitor B:
- Initial charge Q2=24μC
- Final charge QB=32μC
- Charge that flows to B: QflowB=QB−Q2=32μC−24μC=8μC
Final Answer:
The charge that flows through the connecting wire is 8μC.
---
The charge Q on a capacitor is given by the formula:
Q=C×V
where C is the capacitance and V is the voltage.
- Capacitance C1=2μF=2×10−6F
- Voltage V1=12V
- Charge Q1=C1×V1=2×10−6×12=24μC
- Capacitance C2=4μF=4×10−6F
- Voltage V2=6V
- Charge Q2=C2×V2=4×10−6×6=24μC
The total charge Qtotal before connecting the capacitors is:
Qtotal=Q1+Q2=24μC+24μC=48μC
When capacitors are connected positive to positive, they share the total charge until they reach a common potential. The total capacitance Cnet of capacitors in parallel is given by:
Cnet=C1+C2=2μF+4μF=6μF
The common potential Vcommon can be calculated using the formula:
Vcommon=QtotalCnet
Substituting the values:
Vcommon=48μC6μF=8V
Now that we have the common potential, we can find the final charges on each capacitor using the formula Q=C×V.
- QA=C1×Vcommon=2μF×8V=16μC
- QB=C2×Vcommon=4μF×8V=32μC
The charge that flows through the connecting wire is the difference between the initial charge and the final charge on each capacitor.
- Initial charge Q1=24μC
- Final charge QA=16μC
- Charge that flows from A: QflowA=Q1−QA=24μC−16μC=8μC
- Initial charge Q2=24μC
- Final charge QB=32μC
- Charge that flows to B: QflowB=QB−Q2=32μC−24μC=8μC
The charge that flows through the connecting wire is 8μC.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 4 (NCERT EXAMPLAR PROBLEMS)
Explore 6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise-2(C.W)
Explore 53 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
Two capacitors of capacitance 10 μF and 20 μF are charged to potential 20 V and 10 V respectively. If they are connected to share charges, then loss of energy is
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View Solution
Knowledge Check
The charge and energy stored in the capacitor of capacity 32μF, when it is charged to a potential difference of 0.6 kV are respectively
A1.92×10−2C,5.76JB2.92×10−2C,5.76JC1.92×102C,5.76JD1.92×10−2C,4.76JA condenser of capacitance 12μF was initially charged to 20V. Now potential difference is made 40V. The increase in potential energy is
A7.2×10−3JB4×10−3JC3×10−4JD5×10−6JTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
A100B300C1000D3000
Two capacitors A and B with capacities 3μF and 2μF are charged to a potential difference of 100V and 180V, respectively. The plates of the capacitors are connected as show in figure with one wire of each capacitor free. The upper plate of A is positive and that of B is negastive. An uncharged 2μF capcitor C with lead wires falls on the free ends to complete the circuit. Calculate
a. the final charge on the three capacitors.
b. the amount of electrostatic energy stored in the system before and after completion of the circuit.
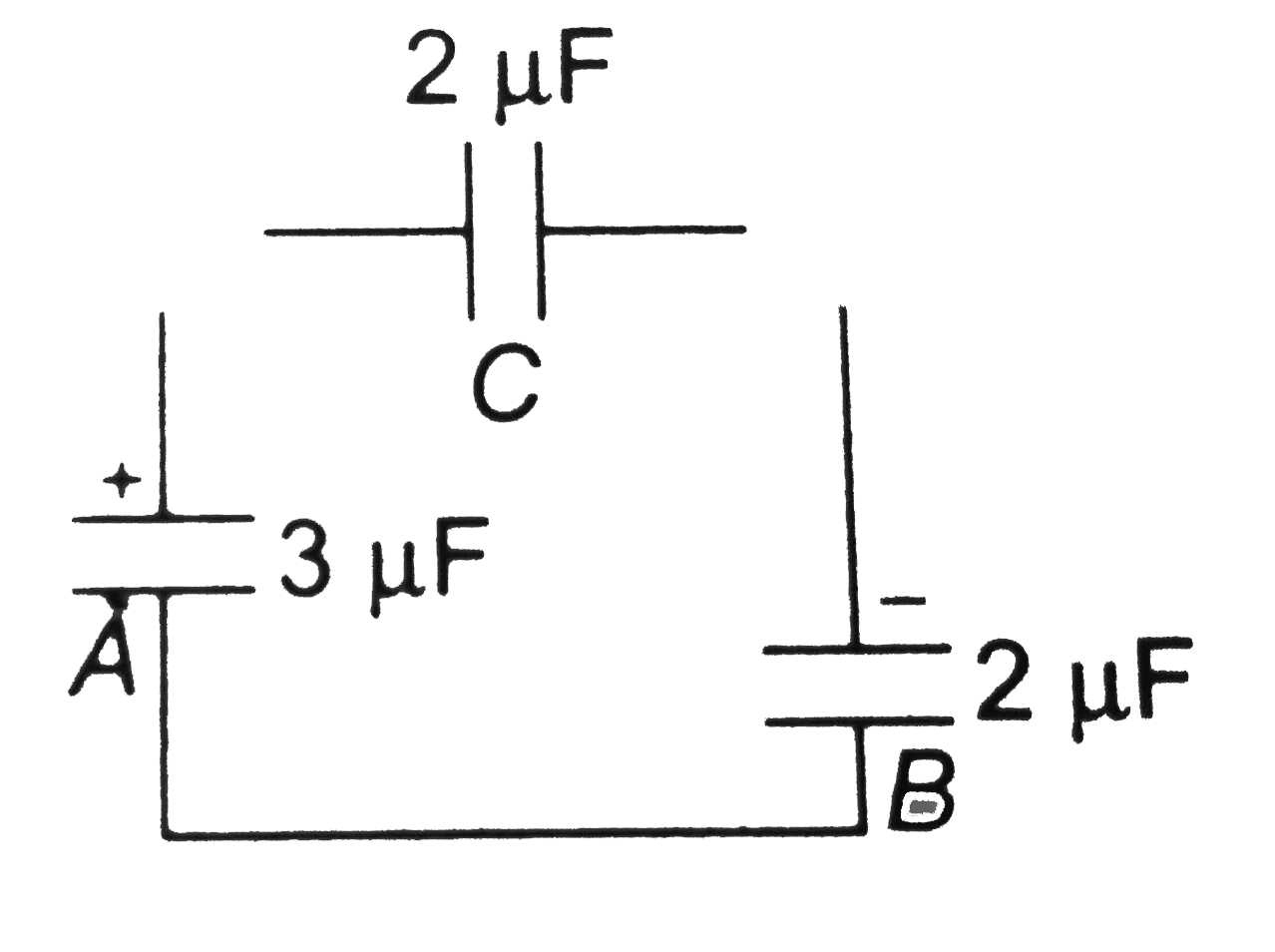
View SolutionTwo capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionThree capacitors of capacitances 1μF,2μF, and 2μF, are cahrged up to the potential difference 30V,10V, and 15V, respectivly. If terminal A is connected with DC is connected with E and F is connected eith B, the find the charge flow in the ciruit and the final charge on the capacitors.
 .
.
View SolutionTwo condensers of capacities 8μF,and4μF are connected in parallel across a potential difference of 120 V. The charge and potential difference across 4μF capacitior is respectively
View Solution

