The longer side of a rectangle is twice the length of its shorter side. A charge q is kept at one vertex. The maximum electric potential due to that charge at any other vertex is V, then the minimum electric potential at any other vertex will be
2V
√3V
V/√5
√5V
The correct Answer is:C
To solve the problem step by step, we will analyze the rectangle and the electric potential due to the charge q at different vertices.
Step 1: Define the rectangle dimensions
Let the length of the shorter side of the rectangle be L. Therefore, the longer side will be 2L.
Step 2: Identify the vertices
Assume the rectangle has vertices at:
- A(0,0) (where the charge q is located)
- B(L,0)
- C(L,2L)
- D(0,2L)
Step 3: Calculate distances from charge q to other vertices
We need to find the distances from charge q at vertex A to the other vertices:
- Distance to vertex B: rAB=L
- Distance to vertex C: rAC=√L2+(2L)2=√L2+4L2=√5L2=L√5
- Distance to vertex D: rAD=2L
Step 4: Calculate electric potential at each vertex
The electric potential V due to a point charge q at a distance r is given by:
V=kqr
where k=14πϵ0.
1. At vertex B:
VB=kqL
2. At vertex C:
VC=kqL√5
3. At vertex D:
VD=kq2L
Step 5: Identify maximum and minimum potentials
From the calculations:
- The maximum potential Vmax occurs at vertex B:
Vmax=kqL
- The minimum potential Vmin occurs at vertex C:
Vmin=kqL√5
Step 6: Relate Vmin to V
Given that the maximum electric potential at any other vertex is V:
V=kqL
Thus, we can express the minimum potential in terms of V:
Vmin=V√5
Final Answer
The minimum electric potential at any other vertex is:
Vmin=V√5
---
Let the length of the shorter side of the rectangle be L. Therefore, the longer side will be 2L.
Assume the rectangle has vertices at:
- A(0,0) (where the charge q is located)
- B(L,0)
- C(L,2L)
- D(0,2L)
We need to find the distances from charge q at vertex A to the other vertices:
- Distance to vertex B: rAB=L
- Distance to vertex C: rAC=√L2+(2L)2=√L2+4L2=√5L2=L√5
- Distance to vertex D: rAD=2L
The electric potential V due to a point charge q at a distance r is given by:
V=kqr
where k=14πϵ0.
VB=kqL
VC=kqL√5
VD=kq2L
From the calculations:
- The maximum potential Vmax occurs at vertex B:
Vmax=kqL
Vmin=kqL√5
Given that the maximum electric potential at any other vertex is V:
V=kqL
Thus, we can express the minimum potential in terms of V:
Vmin=V√5
The minimum electric potential at any other vertex is:
Vmin=V√5
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE -2 (H.W)
Explore 50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise -1 (H.W)
Explore 43 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
[" ABCD is a square,An electric charge + "Q" is kept at the vertex A.The electric intensity at "B" has a "],[" magnitude of "E" .Then the magnitude of the electric intensity at "C" will be "]
View Solution[" ABCD is a square,An electric charge + "Q" is kept at the vertex A.The electric intensity at "B" has a "],[" magnitude of "E" .Then the magnitude of the electric intensity at "C" will be "]
View Solution
Knowledge Check
If the base of a triangle and the ratio of the lengths of the other two unequal sides are given, then the vertex lies on
A. straight lineBcircleCellipseDparabolaA charge +Q at A (see figure) produces electric field E and electric potential V at D. If we now put charges −2Q and +Q at B and C respectively, then the electric field and potential at D will be
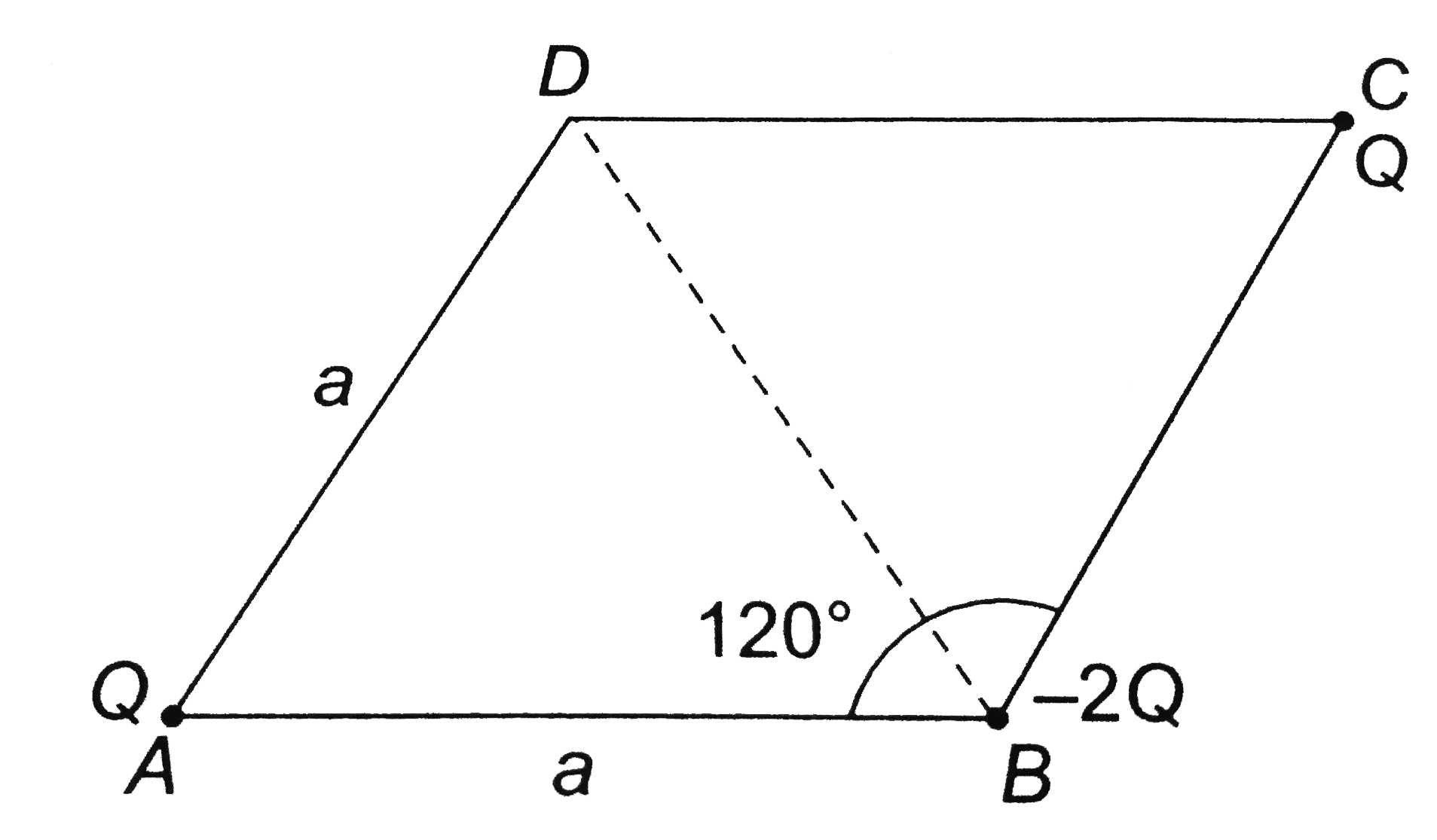 AE and 0B0 and VC√2E and V√2DE√2 and V√2
AE and 0B0 and VC√2E and V√2DE√2 and V√2
If the base of a triangle and the ratio of the lengths of the other two unequal sides are given, then the vertex lies on
View SolutionA charge q is placed at the centre of an imaginary spherical surface. What will be the electric flux due to this charge through any half of the sphere.
View SolutionIf a line through one vertex of a triangle divides the opposite sides in the Ratio of other two sides; then the line bisects the angle at the vertex.
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionA cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
View SolutionIf a charge q is placed at each vertex of a regular polygon, the net electric field at its centre is zero. Show it.
View Solution