A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
We know that the length of diagonal of the cube side b is √3b2=b√3
∴ Distance between center of cube and each vertex, r=b√32
AS V=14π∈0qr
and 8 charges each of value q are present at the eight verticies of the cube, therefore,
V=14π∈08qb√3/2orV=4q√3π∈0b
Further electric field intensity at the center due to all the eight charges is zero, because the fileds due to individual charges cancel in pairs.
Similar Questions
A cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
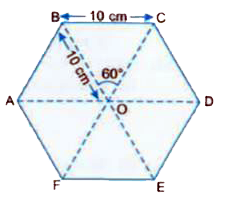
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
View Solution
Knowledge Check
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A0B14π∈0.qa2C14π∈0.6qa2D14π∈0.6q2a2A hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104VA cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
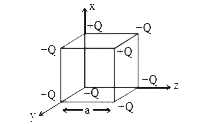 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionA cube of side a has a charge q at each of its vertices. The potential energy of the system, of charges is "(Kq^(2))/(a)((12)/(z)+6sqrt(x)+(4)/(sqrt(y)))." Then find "x+y+z".
View SolutionGiven a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionThe total electric flux through a cube when a charge 8q is placed at one corner of the cube is
View SolutionThe total electric flux through a cube when a charge 8q is placed at one comer of the cube is
View Solution

