Given a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
To calculate the force exerted on any of the charges located at the vertices of a cube due to the other seven charges, we can follow these steps:
Step 1: Identify the Charges and Geometry
We have a cube with point charges q located at each of its vertices. We will calculate the force acting on one of the charges, say charge A.
Step 2: Determine the Distances
The distances between charge A and the other charges are as follows:
- Distance to adjacent charges (1 edge away): A
- Distance to diagonal charges on the same face (2 edges away): √2A
- Distance to the charge directly opposite (3 edges away): √3A
Step 3: Calculate the Forces
Using Coulomb's law, the force F between two point charges is given by:
F=kq2r2
where k=14πϵ0 and r is the distance between the charges.
Forces from Adjacent Charges
For the three adjacent charges (distance A):
Fadj=kq2A2
The direction of these forces will be along the edges of the cube.
Forces from Diagonal Charges
For the three diagonal charges on the same face (distance √2A):
Fdiag=kq2(√2A)2=kq22A2
These forces will be directed diagonally in the plane.
Force from the Opposite Charge
For the charge directly opposite (distance √3A):
Fopp=kq2(√3A)2=kq23A2
This force will be directed towards the opposite vertex.
Step 4: Vector Addition of Forces
Now we need to add these forces as vectors. The forces from the adjacent charges will point along the axes, while the diagonal forces will have components in two directions.
1. Sum of forces from adjacent charges (3 forces):
- Each contributes Fadj along the axes.
- Total force from adjacent charges: 3Fadj^r where ^r is the unit vector along each axis.
2. Sum of forces from diagonal charges (3 forces):
- Each contributes Fdiag at 45∘ to the axes.
- Total force from diagonal charges: 3Fdiag^d where ^d is the diagonal unit vector.
3. Force from the opposite charge:
- This force acts directly towards the opposite vertex.
Step 5: Resultant Force Calculation
The resultant force Fresultant can be calculated by summing all the vector contributions from the adjacent, diagonal, and opposite charges.
Fresultant=Fadj+Fdiag+Fopp
Step 6: Final Expression
After calculating and summing all the forces, we can express the total force acting on charge A due to the other seven charges.
We have a cube with point charges q located at each of its vertices. We will calculate the force acting on one of the charges, say charge A.
The distances between charge A and the other charges are as follows:
- Distance to adjacent charges (1 edge away): A
- Distance to diagonal charges on the same face (2 edges away): √2A
- Distance to the charge directly opposite (3 edges away): √3A
Using Coulomb's law, the force F between two point charges is given by:
F=kq2r2
where k=14πϵ0 and r is the distance between the charges.
For the three adjacent charges (distance A):
Fadj=kq2A2
The direction of these forces will be along the edges of the cube.
For the three diagonal charges on the same face (distance √2A):
Fdiag=kq2(√2A)2=kq22A2
These forces will be directed diagonally in the plane.
For the charge directly opposite (distance √3A):
Fopp=kq2(√3A)2=kq23A2
This force will be directed towards the opposite vertex.
Now we need to add these forces as vectors. The forces from the adjacent charges will point along the axes, while the diagonal forces will have components in two directions.
- Each contributes Fadj along the axes.
- Total force from adjacent charges: 3Fadj^r where ^r is the unit vector along each axis.
- Each contributes Fdiag at 45∘ to the axes.
- Total force from diagonal charges: 3Fdiag^d where ^d is the diagonal unit vector.
- This force acts directly towards the opposite vertex.
The resultant force Fresultant can be calculated by summing all the vector contributions from the adjacent, diagonal, and opposite charges.
After calculating and summing all the forces, we can express the total force acting on charge A due to the other seven charges.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Video
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionA cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
View Solution
Knowledge Check
A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
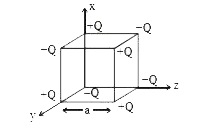 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)A point charge q is kept at a corner of a cube
AElectric flux linked with individual faces of the cube may be zeroBElectric flux linked with individual faces of the cube may be non-zeroCElectric flux linked with a certain face of the cube may be q/8ε0DElectric flux linked with a certain face of the cube may be q/24ε0A regular pentagon has four charges each +q at four of its vertices. At the centre of the pentagon, a charge +q is kept. If the distance of a vertex from the center is a the magnitude of the net force acting on the charge at the center is
Aq24pe0a2BzeroC4q24pe0a2D2q24pe0a2
Eight point charges , each q , are placed on the vertices of a cube of side a. Find the potential energy of the system of charges.
View SolutionThree identical point charges q are kept on each vertices of an equilateral triangle of side a. Calculate the work done in slowly moving the charges to the mid points of each side, covering the shortest possible distance.
View SolutionDoes the force on a charge due to another charge depend on the charges present nearby?
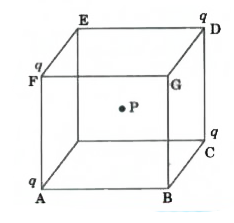
View SolutionFour identical charged particles of charge q are kept on the vertices of a cube with side 20 cm as shown in the figure. Calcualte the electric potential at point P in the centre of the cube due to all these charges.
View SolutionAssertion :The force with which two charges attract or repel each other are not affected by the presence of a third charge.
Reason : Force on any charge due to a number of other charges is the vector sum of all the forces on that charge due to other charges, taken one at a time.
View Solution