Eight point charges , each , are placed on the vertices of a cube of side . Find the potential energy of the system of charges.
To find the potential energy of a system of eight point charges, each of charge q, placed at the vertices of a cube with side length a, we can follow these steps:
Step 1: Determine the number of unique pairs of charges
The total number of unique pairs of charges can be calculated using the combination formula (n2), where n is the number of charges. For 8 charges, the number of pairs is:
Number of pairs=(82)=8×72=28
Step 2: Classify the pairs based on their separation distances
In a cube, the pairs of charges can be classified based on their separation distances:
1. Side length pairs: Charges that are separated by a distance a.
2. Face diagonal pairs: Charges that are separated by a distance √2a.
3. Body diagonal pairs: Charges that are separated by a distance √3a.
Step 3: Count the number of pairs for each type of separation
1. Pairs separated by side length a: Each edge of the cube has 1 pair, and there are 12 edges.
- Total pairs = 12
2. Pairs separated by face diagonal √2a: Each face has 2 diagonals, and there are 6 faces.
- Total pairs = 2×6=12
3. Pairs separated by body diagonal √3a: There are 4 body diagonals in a cube.
- Total pairs = 4
Step 4: Calculate the potential energy contribution from each type of pair
The potential energy U between two point charges q separated by a distance r is given by:
U=kq2r
where k is Coulomb's constant.
1. For side length pairs (12 pairs):
Uside=12×kq2a
2. For face diagonal pairs (12 pairs):
Uface=12×kq2√2a=12kq2√2a
3. For body diagonal pairs (4 pairs):
Ubody=4×kq2√3a=4kq2√3a
Step 5: Sum the contributions to find the total potential energy
Now, we can sum the contributions from all types of pairs:
Utotal=Uside+Uface+Ubody
Utotal=12kq2a+12kq2√2a+4kq2√3a
Step 6: Factor out common terms
Factoring out kq2a:
Utotal=kq2a(12+12√2+4√3)
Final Result
Thus, the potential energy of the system of charges is:
Utotal=kq2a(12+12√2+4√3)
The total number of unique pairs of charges can be calculated using the combination formula (n2), where n is the number of charges. For 8 charges, the number of pairs is:
Number of pairs=(82)=8×72=28
In a cube, the pairs of charges can be classified based on their separation distances:
1. Side length pairs: Charges that are separated by a distance a.
2. Face diagonal pairs: Charges that are separated by a distance √2a.
3. Body diagonal pairs: Charges that are separated by a distance √3a.
1. Pairs separated by side length a: Each edge of the cube has 1 pair, and there are 12 edges.
- Total pairs = 12
2. Pairs separated by face diagonal √2a: Each face has 2 diagonals, and there are 6 faces.
- Total pairs = 2×6=12
3. Pairs separated by body diagonal √3a: There are 4 body diagonals in a cube.
- Total pairs = 4
The potential energy U between two point charges q separated by a distance r is given by:
U=kq2r
where k is Coulomb's constant.
Uside=12×kq2a
Uface=12×kq2√2a=12kq2√2a
Ubody=4×kq2√3a=4kq2√3a
Now, we can sum the contributions from all types of pairs:
Utotal=Uside+Uface+Ubody
Utotal=12kq2a+12kq2√2a+4kq2√3a
Factoring out kq2a:
Utotal=kq2a(12+12√2+4√3)
Thus, the potential energy of the system of charges is:
Utotal=kq2a(12+12√2+4√3)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
A18×10−6JB9JC9×10−6JD27J
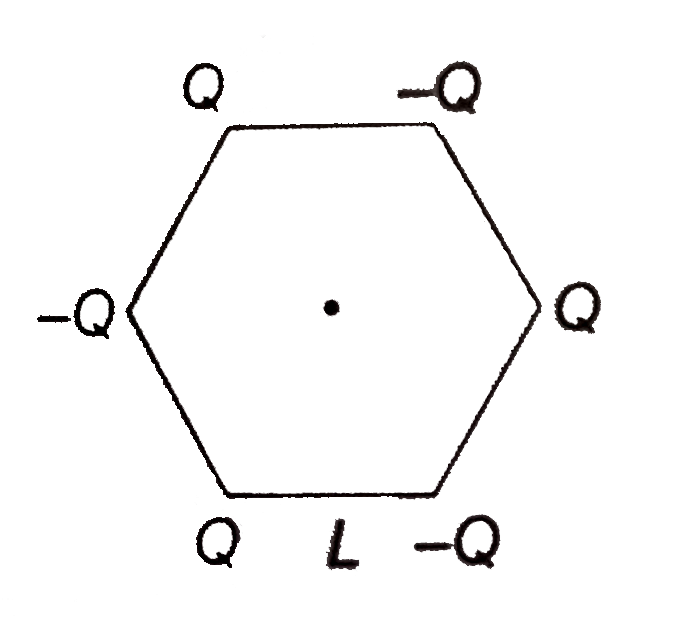
Six equal point charges q each are placed at six corners of a hexago of side a. Find out potential energy of charge system

View SolutionEight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
 .
.
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionEight equal point charges each of charge 'q' and mass 'm' are placed at eight corners of a cube of side 'a'.
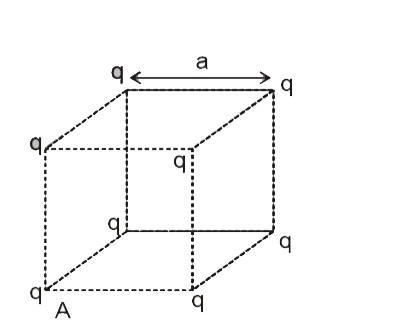
(i) Find out potential energy of charge system.
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
potential energy of this system .
View SolutionFive point charges, each +q are placed on five vertices of a regular hexagon of side' l '. Find the magnitude of the resultant force on a charge –q placed at the centre of the hexagon.
View Solution