Calculate the electric field at origin due to infinite number of charges as shown in figure below.

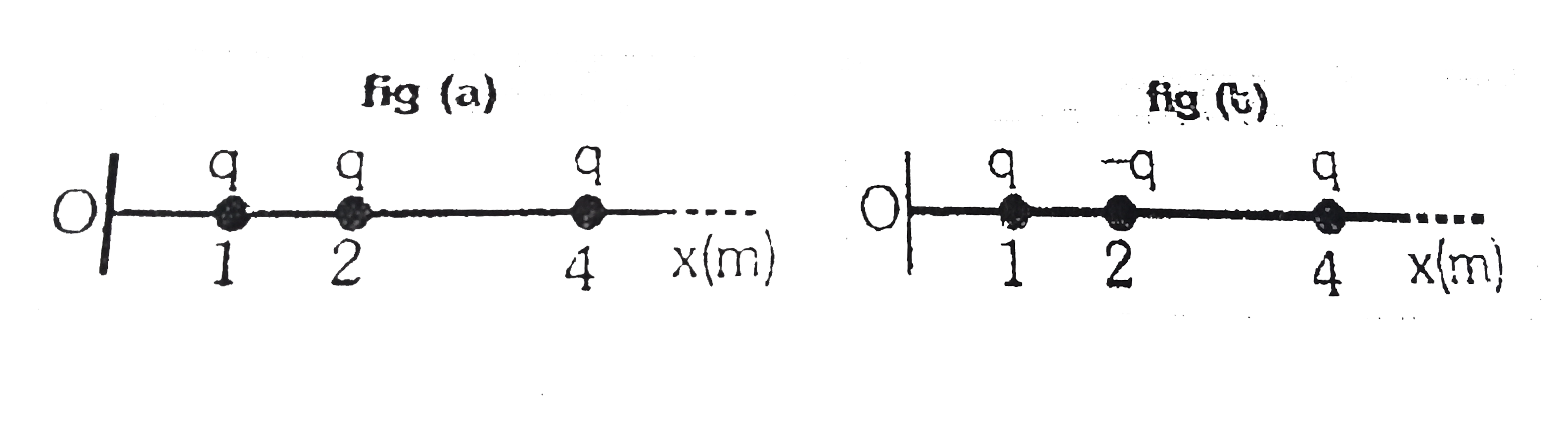
Video Solution

Text Solution

Verified by Experts

(a) $E_{0} = k q [\frac{1}{1} + \frac{1}{4} + \frac{1}{16} + - - - -] = \frac{k q . 1}{(1 - 1 / 4)} = \frac{4 k q}{3} [∵ S_{\infty} = \frac{a}{1 - r}, a = 1 and r = \frac{1}{4}]$
(b) $E_{0} = k q [\frac{1}{1} - \frac{1}{4} + \frac{1}{16} - - - - -] = \frac{k q . 1}{(1 - (- 1 / 4))} = \frac{4 k q}{5}$

Updated on:21/07/2023

|

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Electric field , due to an infinite line of change, as shown in figure at a point $P$ at a distance $r$ from the line is $E$ . If wire is folded at point $A$ , so that both parts lie alongside as shown in figure(b), then express electric field at $P$ in vector form.

A $\frac{E}{2} ˆ i + \frac{E}{2} ˆ j$
B $E ˆ i + E ˆ j$
C $\sqrt{2} E ˆ i + \sqrt{2} E ˆ j$
D $\frac{E}{\sqrt{2}} ˆ i + \frac{E}{\sqrt{2}} ˆ j$
The electric field on two sides of a thin sheet of charge is shown in the figure. The charge density on the sheet is

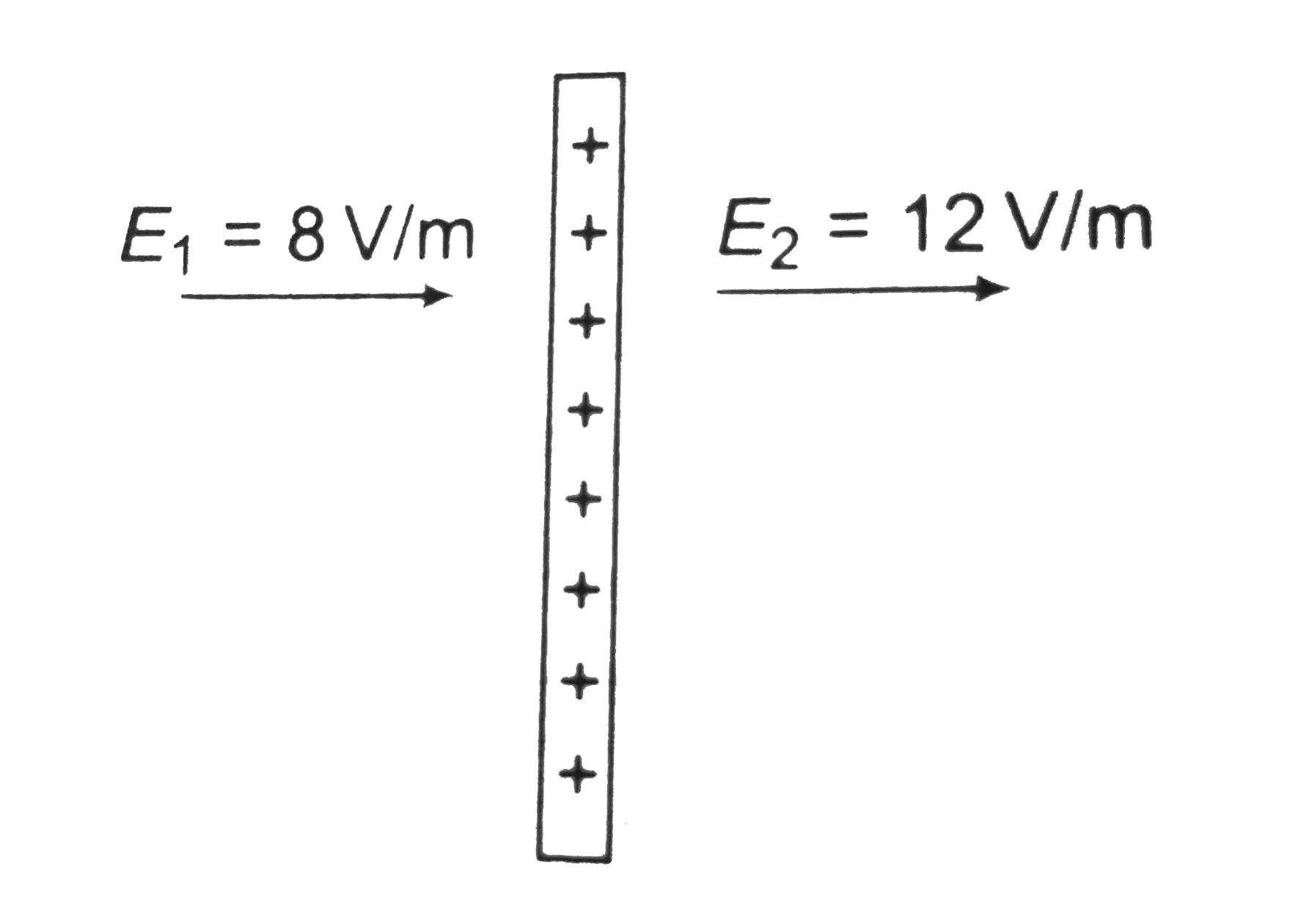A $2 ε_{0}$
B $4 ε_{0}$
C $10 ε_{0}$
Dzero
The spatial distribution of the electric field due to charges $(A, B)$ is shown in figure. Which of the following statements is correct?

A $A$ is $+ v e$ and $B - v e$ and $| A | > | B |$
B $A$ is $- v e$ and $B + v e, | A | = | B |$
CBoth are $+ v e$ but $A > B$
DBoth are $- v e$ but $A > B$

ALLEN-MISCELLANEOUS-Part -II Example

Home
Ask Doubt
Profile