A uniform electric field 400NC acts along positive y-axis, P is a point having co-ordinates (0.6m,-0.2m) and R another point, with co-ordinates (-0.4m, 0.6m). If electric potential at P is 200V, potential at R will be.
100
−150V
80V
−120V
The correct Answer is:D
To find the electric potential at point R given the electric potential at point P and the uniform electric field, we can follow these steps:
Step 1: Understand the electric field and its direction
The electric field E is given as 400N/C acting along the positive y-axis. This means that the electric field vector can be represented as:
→E=400^jN/C
Step 2: Identify the coordinates of points P and R
The coordinates of point P are (0.6m,−0.2m) and the coordinates of point R are (−0.4m,0.6m).
Step 3: Calculate the change in the y-coordinate
To find the change in potential between points P and R, we need to calculate the change in the y-coordinate:
- The y-coordinate of point P is −0.2m.
- The y-coordinate of point R is 0.6m.
The change in y-coordinate (Δy) is:
Δy=yR−yP=0.6−(−0.2)=0.6+0.2=0.8m
Step 4: Use the formula for potential difference
The potential difference ΔV between two points in an electric field is given by:
ΔV=−EΔy
Here, E=400N/C and Δy=0.8m.
Substituting the values:
ΔV=−400×0.8=−320V
Step 5: Relate the potentials at points P and R
We know that:
VR−VP=ΔV
Substituting the known values:
VR−200=−320
Step 6: Solve for the potential at point R
Rearranging the equation to find VR:
VR=−320+200=−120V
Final Answer
The electric potential at point R is:
−120V
The electric field E is given as 400N/C acting along the positive y-axis. This means that the electric field vector can be represented as:
→E=400^jN/C
The coordinates of point P are (0.6m,−0.2m) and the coordinates of point R are (−0.4m,0.6m).
To find the change in potential between points P and R, we need to calculate the change in the y-coordinate:
- The y-coordinate of point P is −0.2m.
- The y-coordinate of point R is 0.6m.
Δy=yR−yP=0.6−(−0.2)=0.6+0.2=0.8m
The potential difference ΔV between two points in an electric field is given by:
ΔV=−EΔy
Here, E=400N/C and Δy=0.8m.
ΔV=−400×0.8=−320V
We know that:
VR−VP=ΔV
Substituting the known values:
VR−200=−320
Rearranging the equation to find VR:
VR=−320+200=−120V
The electric potential at point R is:
−120V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE -2 (H.W)
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise -1 (H.W)
43 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
A uniform electric field of 30NC−1 exists along the X-axis calculate the potential difference VB−VA between the points A (4m,2m) and B(10m,5m).
View SolutionA uniform electric field of magnitude 325Vm−1 is directed in the negative y - direction in (fig. 3.12). Theb coordinates of point A are (−0.2m,−0.3m) and those of point B are (0.4m,0.5m). Calculate the potential difference VB−VA along the path shown in the figure.
 .
.
View Solution
Knowledge Check
Moment of a force of magnitude 10 N acting along positive y-direction at point (2m,0,0) about the point (0,1m,0) in N-m is
A10B20C10√2D30A uniform electric field Eˆi exists in a region containing the orign of co-ordinate system. The points A(a,0,0),B(0,a,0) and C(0,0,a) are on the co-ordinate axes. The magnitude of electric flux through the trianglular area ABC is
A2Ea2BEa2/2CzeroDEa2Moment of a force of magnitude 20 N acting along positive x-direction at point (3m,0,0) about the point (0,2,0) (in N-m) is
A20B60C40D30
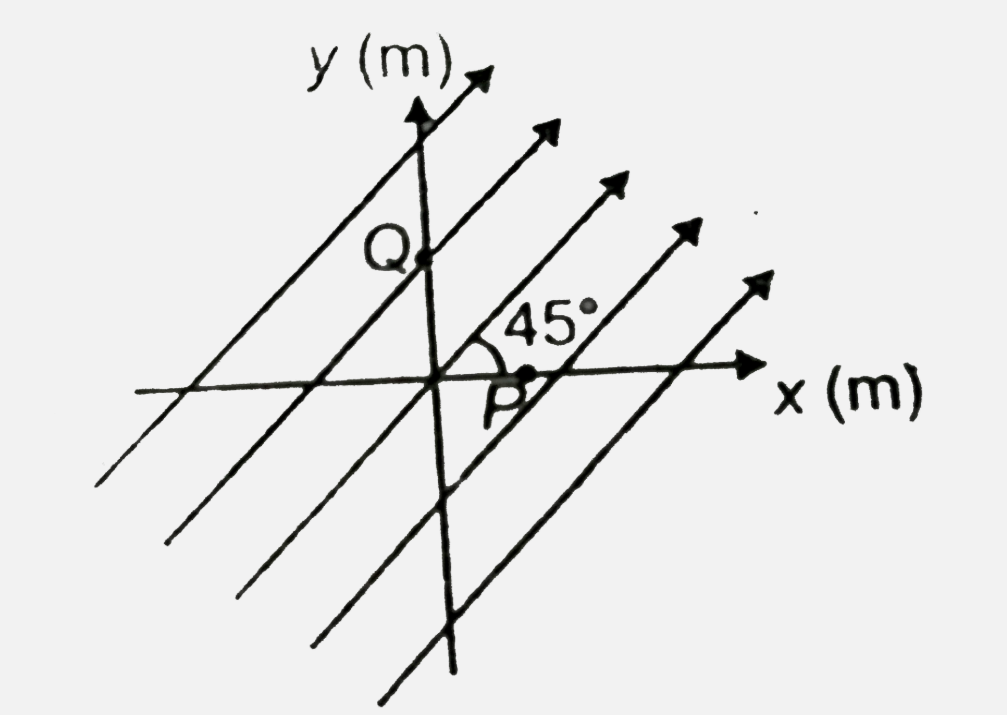
A uniform electric field of 200 V / m is directed at 45∘ with x -axis as shown in figure. The co-ordinates of point P and point Q are (1,0) and ( 0,2) . Find the potential difference , VP−VQ ( in volts) .
View SolutionA uniform electric field is along x-axis. The potential difference VA−VB=10V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionA uniform electric field of 100V/m is directed at 30∘ with the positive x-axis as shown in figure. Find the potential difference VBA if OA=2m and OB=4m.

View SolutionMoment of a force of megnitude 20 N acting along positive x direction at point (3m 0, 0) about the point (0, 2, 0) (in N-m) is :-
View SolutionThe magnitude of electric field intensity at a point on the axis of short dipole is 30V/m. The distance of the point from the centre of the dipole is 2m. Then potential at that point is
View Solution
