Two identical pendulums A an dB are suspended from the same point. Both are givne positive charge, with A having more charge than B. They diverge and reach equilibrium with the suspension of A and B making angles θ1 and θ2 with the vertical respectively.
θ1>θ2
θ1<θ2
θ1=θ2
The tension in A is greater than that in B
The correct Answer is:C
To solve the problem of the two identical pendulums A and B that are suspended from the same point and given positive charges, we need to analyze the forces acting on each pendulum and their equilibrium conditions.
1. Understanding the Setup:
- Two identical pendulums A and B are suspended from the same point.
- Pendulum A has a charge Q (greater charge) and pendulum B has a charge q (smaller charge).
- Both pendulums make angles θ1 and θ2 with the vertical, respectively.
2. Electrostatic Force:
- Since both charges are positive, they will repel each other due to electrostatic force.
- The electrostatic force F between them can be expressed using Coulomb's law:
F=kQqd2
where k is Coulomb's constant and d is the distance between the two charges.
3. Forces Acting on the Pendulums:
- For pendulum A:
- The tension T1 acts along the string.
- The weight mg acts downward.
- The electrostatic force F acts horizontally away from B.
- For pendulum B:
- The tension T2 acts along the string.
- The weight mg acts downward.
- The electrostatic force F acts horizontally away from A.
4. Equilibrium Conditions:
- For pendulum A:
- Vertical component:
T1cosθ1=mg
- Horizontal component:
T1sinθ1=F
- For pendulum B:
- Vertical component:
T2cosθ2=mg
- Horizontal component:
T2sinθ2=F
5. Relating the Tensions and Angles:
- From the vertical components, we have:
T1cosθ1=T2cosθ2
- From the horizontal components, we have:
T1sinθ1=T2sinθ2
6. Dividing the Equations:
- Dividing the horizontal and vertical equations gives:
T1sinθ1T1cosθ1=T2sinθ2T2cosθ2
- This simplifies to:
tanθ1=tanθ2
- Therefore, we conclude that:
θ1=θ2
7. Conclusion:
- Since the angles θ1 and θ2 are equal, it implies that the tensions T1 and T2 must also be equal, given that the masses of the pendulums are identical.
- Thus, the answer to the question is that θ1=θ2.
- Two identical pendulums A and B are suspended from the same point.
- Pendulum A has a charge Q (greater charge) and pendulum B has a charge q (smaller charge).
- Both pendulums make angles θ1 and θ2 with the vertical, respectively.
- Since both charges are positive, they will repel each other due to electrostatic force.
- The electrostatic force F between them can be expressed using Coulomb's law:
F=kQqd2
where k is Coulomb's constant and d is the distance between the two charges.
- For pendulum A:
- The tension T1 acts along the string.
- The weight mg acts downward.
- The electrostatic force F acts horizontally away from B.
- For pendulum B:
- The tension T2 acts along the string.
- The weight mg acts downward.
- The electrostatic force F acts horizontally away from A.
- For pendulum A:
- Vertical component:
T1cosθ1=mg
- Horizontal component:
T1sinθ1=F
- For pendulum B:
- Vertical component:
T2cosθ2=mg
- Horizontal component:
T2sinθ2=F
- From the vertical components, we have:
T1cosθ1=T2cosθ2
- From the horizontal components, we have:
T1sinθ1=T2sinθ2
- Dividing the horizontal and vertical equations gives:
T1sinθ1T1cosθ1=T2sinθ2T2cosθ2
- This simplifies to:
tanθ1=tanθ2
- Therefore, we conclude that:
θ1=θ2
- Since the angles θ1 and θ2 are equal, it implies that the tensions T1 and T2 must also be equal, given that the masses of the pendulums are identical.
- Thus, the answer to the question is that θ1=θ2.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -1 (C.W)
Explore 24 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -1 (H.W)
Explore 27 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EVALUATE YOURSELF-4
Explore 6 Videos
- DUAL NATUREBook:NARAYNAChapter:DUAL NATUREExercise:LEVEL-II (H.W)
Explore 17 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Level-II (H.W)
Explore 23 Videos
Similar Questions
Two identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
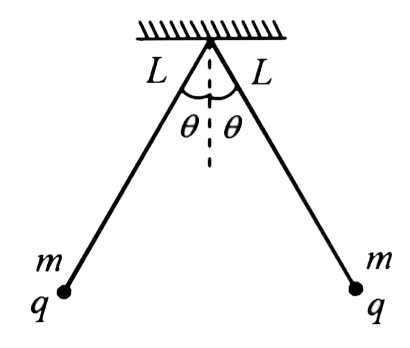
View Solution
Knowledge Check
Two identical pendulums A an dB are suspended from the same point. Both are givne positive charge, with A having more charge than B. They diverge and reach equilibrium with the suspension of A and B making angles θ1 and θ2 with the vertical respectively.
Aθ1>θ2Bθ1<θ2Cθ1=θ2DThe tension in A is greater than that in BTwo identical simple pendulums P and Q are susupended from a common point. The bobs of both the pendulums are positively charged but the magnitude of charge on the bob of P is double to that on Q, Both the bobs repel and reach equilibrium. If the thread of P makes an angle θ1 with the vertical and that of Q make an angle θ2 with the vertical, then
Aθ1>θ2Bθ1=θ2Cθ1<θ2DInformation insufficientTwo positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
Aq1m2=q2m2Bm1=m2Cm1=m2sinθDq2m1=q1m2
Two small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
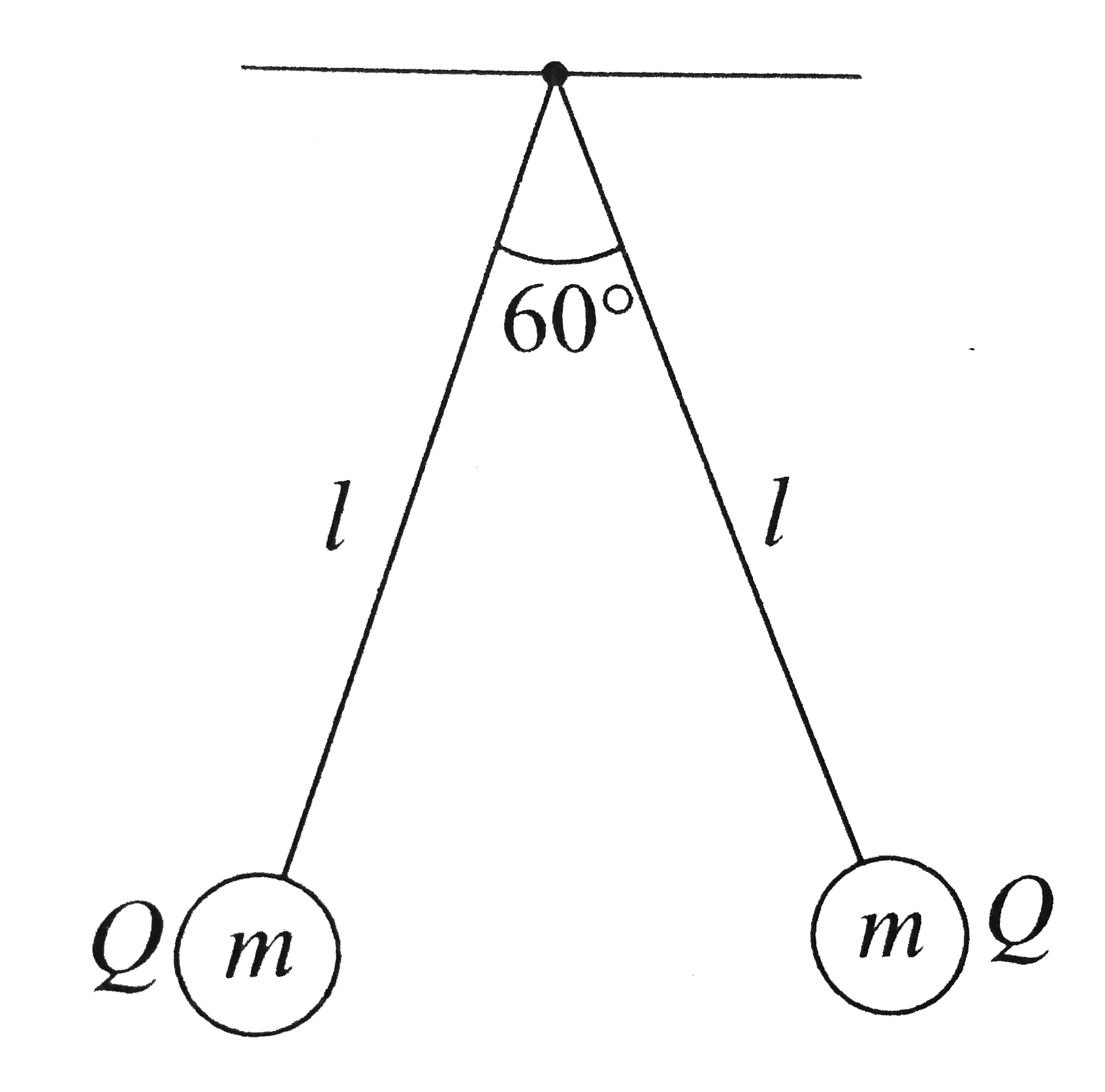
View SolutionTwo identical beam A and B of plane coherent waves of the sasme intensity and wavelength λ fall on a plane screen. The direction of the beam propagations make angles θ1 and θ2 with the normal to the screen and lie in the same plane as shown in the figure. Find the distance β between adject interfrence fringes on the screen.

View SolutionTwo positively charged spheres of masses m1, and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charged on the two spheres are q1 and q2, respectively. At equilibrium both strings make the same angle θ with the vertical. Then
View SolutionTwo small equal point charges of magnitude q are suspended from a common point on the ceiling by insulating mass less strings of equal lengths. They come to equilibrium with each string making angle θ from the vertical. If the mass of each charge is m, then the electrostatic potential at the centre of line joining the will be (14πεlion0=k)
View SolutionTwo projectiles A and B are thrown with the same speed such that A makes angle θ with the horizontal and B makes angle θ with the vertical, then -
View Solution