Question

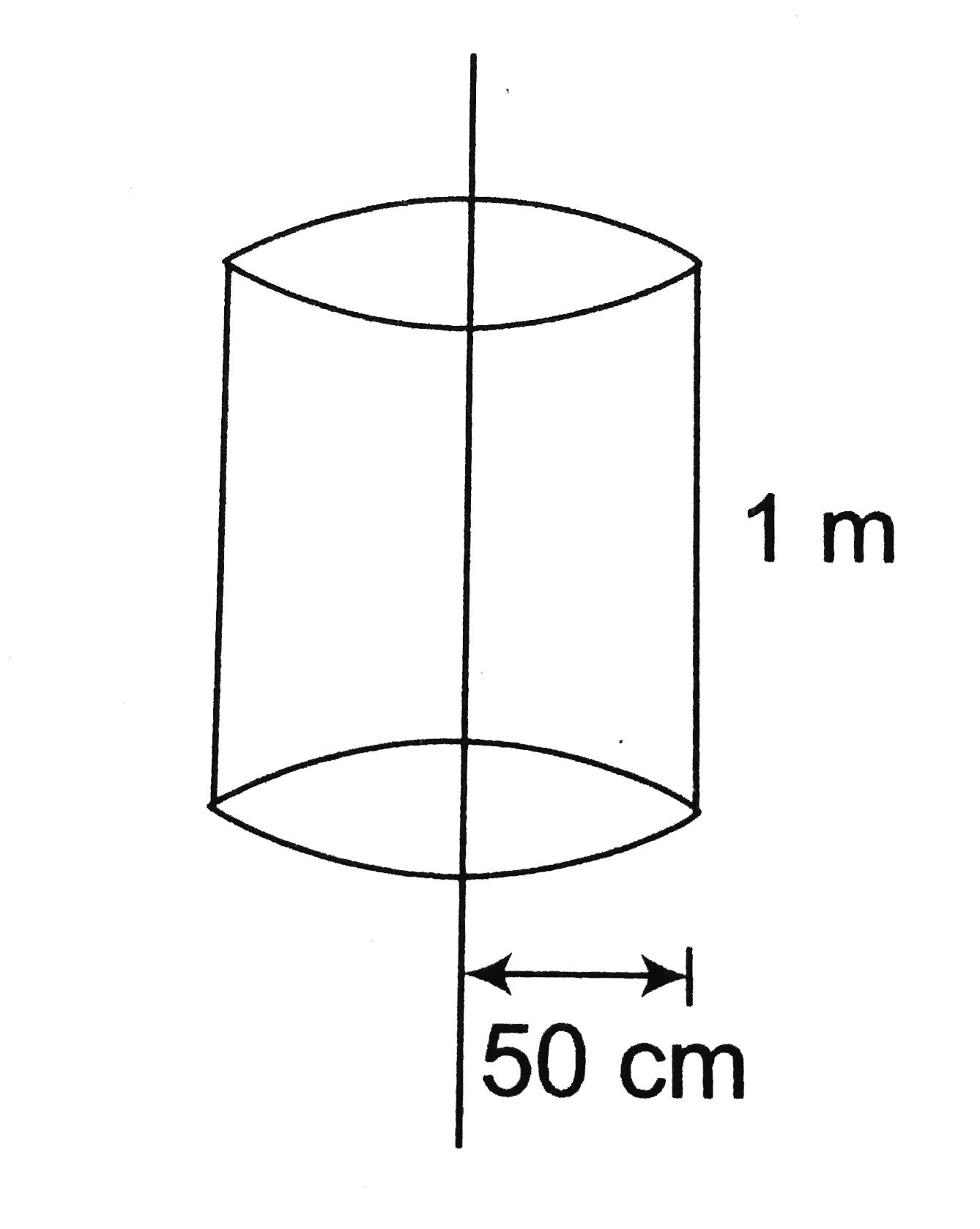
Electric charge is uniformly distributed along a long straight wire of radius 1 mm. The charge per cm length of the wire Q coulomb. Another cylindrical surface of radius 50 cm and length 1 m symmetrical encloses the wire as shown in the figure. The total electric flux passing through the cylindrical surface is

Options

A. `Q/(epsilon_(0))`
B. `(100Q)/(epsilon_(0))`
C. `(100Q)/((epsilon_(0))^(2))`
D. `(100Q)/((piepsilon_(0)))`

Answer

B

Explanation

To find the total electric flux passing through the cylindrical surface that encloses a long straight wire with a uniform charge distribution, we can use Gauss's law. Here's a step-by-step solution:

Step 1: Understand the Given Information
- The wire has a uniform charge distribution with charge per unit length \( Q \) (in coulombs per centimeter).
- The radius of the wire is \( 1 \, \text{mm} \) (which is not directly needed for the calculation).
- The cylindrical surface that encloses the wire has a radius of \( 50 \, \text{cm} \) and a length of \( 1 \, \text{m} \).

Step 2: Apply Gauss's Law
Gauss's law states that the total electric flux \( \Phi_E \) through a closed surface is equal to the charge enclosed \( Q_{\text{enc}} \) divided by the permittivity of free space \( \epsilon_0 \):
\( \Phi_E = \frac{Q_{\text{enc}}}{\epsilon_0} \)

Step 3: Calculate the Charge Enclosed
The charge per unit length of the wire is \( Q \) (coulombs per cm). To find the total charge enclosed by the cylindrical surface, we need to calculate the charge along the length of the cylinder:
- The length of the cylindrical surface is \( 1 \, \text{m} = 100 \, \text{cm} \).
- Therefore, the total charge \( Q_{\text{enc}} \) enclosed by the cylindrical surface is:
\( Q_{\text{enc}} = Q \times \text{length of the cylinder} = Q \times 100 \, \text{cm} = 100Q \, \text{coulombs} \)

Step 4: Substitute into Gauss's Law
Now, substitute \( Q_{\text{enc}} \) into Gauss's law:
\( \Phi_E = \frac{100Q}{\epsilon_0} \)

Step 5: Conclusion
Thus, the total electric flux passing through the cylindrical surface is:
\( \Phi_E = \frac{100Q}{\epsilon_0} \)

Final Answer
The correct option is \( 100Q/\epsilon_0 \).

---