Consider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
We can divide the entire surface into three parts, right and left plane faces and curved portion of its surface. Hence, the surface integral consists of the sum of the three terms:
ϕE=∮E⋅dA=∫leftendE⋅dA+∫rightendE⋅dA+∫curvedE⋅dA
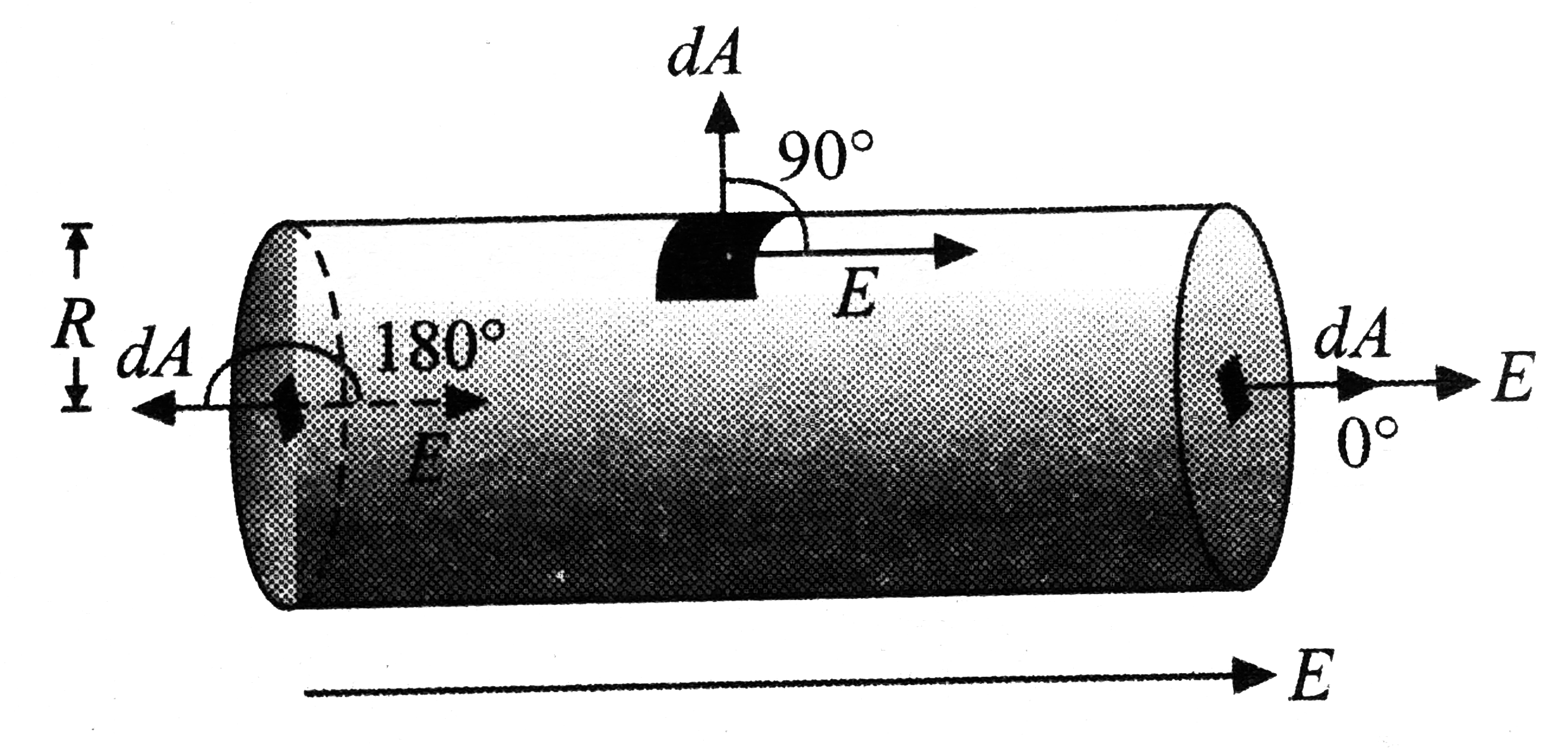
All the area elements on the left end and electric field E are
at and angle of 180∘.
(ϕE)leftend=∮leftendE⋅dA=∮leftendEdAcos180∘
=−E∮rightenddA=EπR2
Note that E is constant over the entire plane surface of left end, therefore, we take it out from the integral.
Similarly, all the area elements on the right end are parallel
to electric field E, i.e., angle is 0∘.
(ϕE)rightend=∮rightendE⋅dA=∮rightendEdAcos0∘
=+E∮rightenddA=EπR2
Finally, at every point on the curved surface the area vectors
are perpendicular to the direction of the electric field. Thus,
(ϕE)curved=∮curvedsurfaceE⋅dA=∮curvedsurfaceEdA(cos90∘)=0
Total flux =(ϕE)rightend+(ϕE)leftend+(ϕE)curvedsurface
=(+EπR2)+(−EπR2)+0=0
Hence, we see that in a uniform field the flux through a closed surface is zero. This is true for any shape of closed surface.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Example
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
A cylinder of radius r and length l is placed in an uniform electric field parallel to the axis of the cylinder. The total flux for the surface of the cylinder is given by-
View SolutionA cyclinder of radius r and length l is placed in an uniform electric field in such a way that the axis of the cyclinder is parallel to the field. The flux of the field through the cyclindrical surface is
View Solution
Knowledge Check
In figure, a cone lies in a uniform electric field E. Determine the electric flux entering the cone.
 . AERh2B0C2ERhDErh
. AERh2B0C2ERhDErhA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
A2πR2EBπR2/EC(πR2−πR)EDzeroA cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
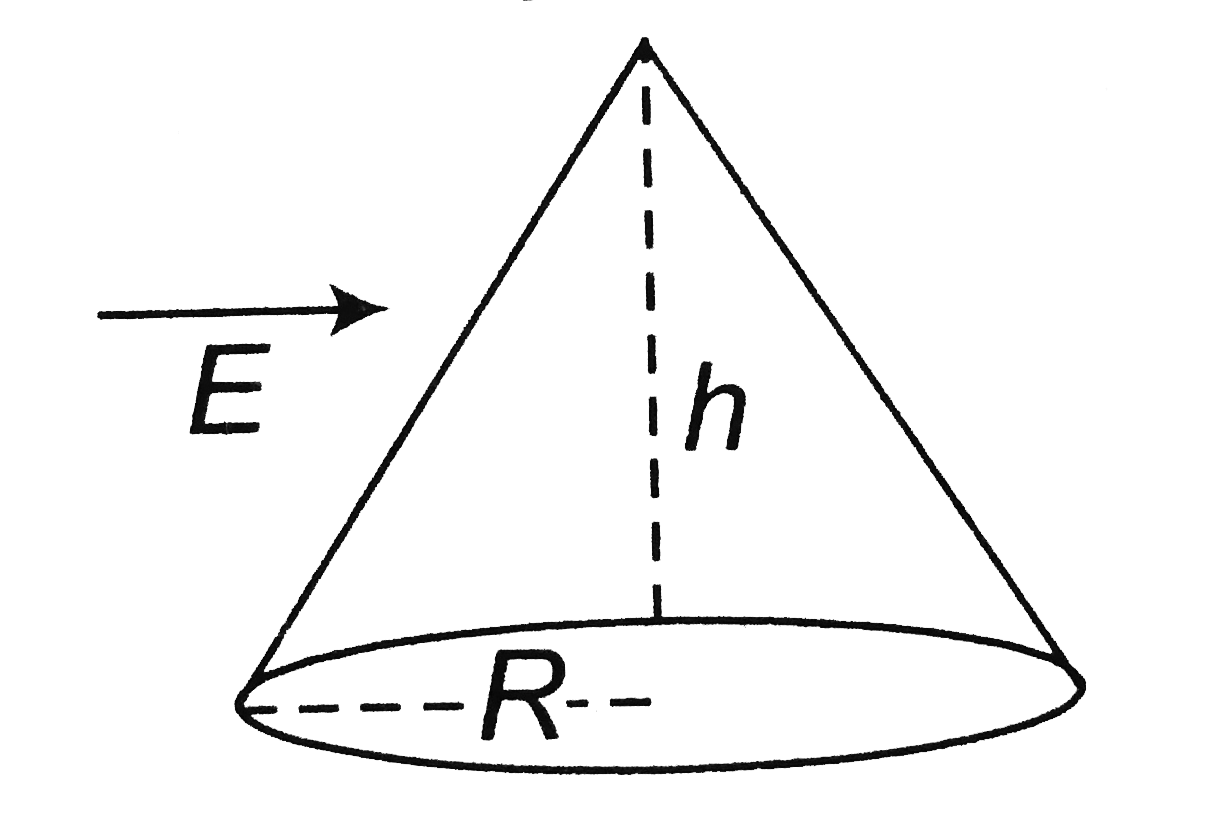 AEπR2BERhCEhR2DEh2
AEπR2BERhCEhR2DEh2
A cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
View SolutionThe electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
View Solution

