A hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
πr2E
2πrE2
4πr2E
4πrE2
The correct Answer is:a
To find the electric flux passing through a hemispherical bowl of radius r placed in a uniform electric field E, we can follow these steps:
Step 1: Understand the Concept of Electric Flux
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which the field lines pass, taking into account the angle (θ) between the electric field and the normal (area vector) to the surface. Mathematically, it is given by:
Φ=E⋅A⋅cos(θ)
Step 2: Analyze the Orientation of the Electric Field
The orientation of the electric field relative to the hemispherical bowl is crucial. There are two main cases to consider:
1. Electric Field Parallel to the Flat Surface of the Hemisphere: In this case, the electric field lines run parallel to the flat circular base of the hemisphere.
2. Electric Field Perpendicular to the Flat Surface of the Hemisphere: Here, the electric field lines are directed straight through the center of the hemisphere.
Step 3: Case 1 - Electric Field Parallel to the Flat Surface
If the electric field is parallel to the flat surface of the hemisphere:
- The angle θ between the electric field and the area vector of the flat surface is 90∘.
- Therefore, cos(90∘)=0.
- The electric flux through the hemispherical bowl is:
Φ=E⋅A⋅cos(90∘)=E⋅A⋅0=0
Thus, the electric flux through the hemispherical bowl is zero in this orientation.
Step 4: Case 2 - Electric Field Perpendicular to the Flat Surface
If the electric field is perpendicular to the flat surface of the hemisphere:
- The angle θ between the electric field and the area vector of the flat surface is 0∘.
- Therefore, cos(0∘)=1.
- The area A of the circular base of the hemisphere is πr2.
- The electric flux through the hemispherical bowl is:
Φ=E⋅A⋅cos(0∘)=E⋅(πr2)⋅1=E⋅πr2
Conclusion
The electric flux passing through the hemispherical bowl depends on the orientation of the electric field:
- If the electric field is parallel to the flat surface, the flux is 0.
- If the electric field is perpendicular to the flat surface, the flux is E⋅πr2.
Final Answer
The electric flux passing through the hemispherical bowl is:
Φ=E⋅πr2(if perpendicular)
Φ=0(if parallel)
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which the field lines pass, taking into account the angle (θ) between the electric field and the normal (area vector) to the surface. Mathematically, it is given by:
Φ=E⋅A⋅cos(θ)
The orientation of the electric field relative to the hemispherical bowl is crucial. There are two main cases to consider:
1. Electric Field Parallel to the Flat Surface of the Hemisphere: In this case, the electric field lines run parallel to the flat circular base of the hemisphere.
2. Electric Field Perpendicular to the Flat Surface of the Hemisphere: Here, the electric field lines are directed straight through the center of the hemisphere.
If the electric field is parallel to the flat surface of the hemisphere:
- The angle θ between the electric field and the area vector of the flat surface is 90∘.
- Therefore, cos(90∘)=0.
- The electric flux through the hemispherical bowl is:
Φ=E⋅A⋅cos(90∘)=E⋅A⋅0=0
Thus, the electric flux through the hemispherical bowl is zero in this orientation.
If the electric field is perpendicular to the flat surface of the hemisphere:
- The angle θ between the electric field and the area vector of the flat surface is 0∘.
- Therefore, cos(0∘)=1.
- The area A of the circular base of the hemisphere is πr2.
- The electric flux through the hemispherical bowl is:
Φ=E⋅A⋅cos(0∘)=E⋅(πr2)⋅1=E⋅πr2
The electric flux passing through the hemispherical bowl depends on the orientation of the electric field:
- If the electric field is parallel to the flat surface, the flux is 0.
- If the electric field is perpendicular to the flat surface, the flux is E⋅πr2.
The electric flux passing through the hemispherical bowl is:
Φ=E⋅πr2(if perpendicular)
Φ=0(if parallel)
Topper's Solved these Questions
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:WB JEE / WORKOUT) CATEGORY 2 : Single Option Correct Type (2 Marks)
Explore 15 Videos
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE / WORKOUT )CATEGORY 3 : One or More than One Option Correct Type (2 Marks)
Explore 10 Videos
- ELECTROMAGNETIC WAVES Book:MTG-WBJEEChapter:ELECTROMAGNETIC WAVES Exercise:WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
Explore 10 Videos
- GRAVITATIONBook:MTG-WBJEEChapter:GRAVITATIONExercise:WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
Explore 7 Videos
Similar Questions
Knowledge Check
A hemispherical body of radius R is placed in a uniform electric field E. If the field E is parallel to the base of the hemisphere the flux linked with it is
A2πREB2πR2ECπR2EDzeroA hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
Aϕ=(E(πR)Bϕ=(ES=E(πR3)Cϕ=E(πR2)Dϕ=(ES=E(πR4)A cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
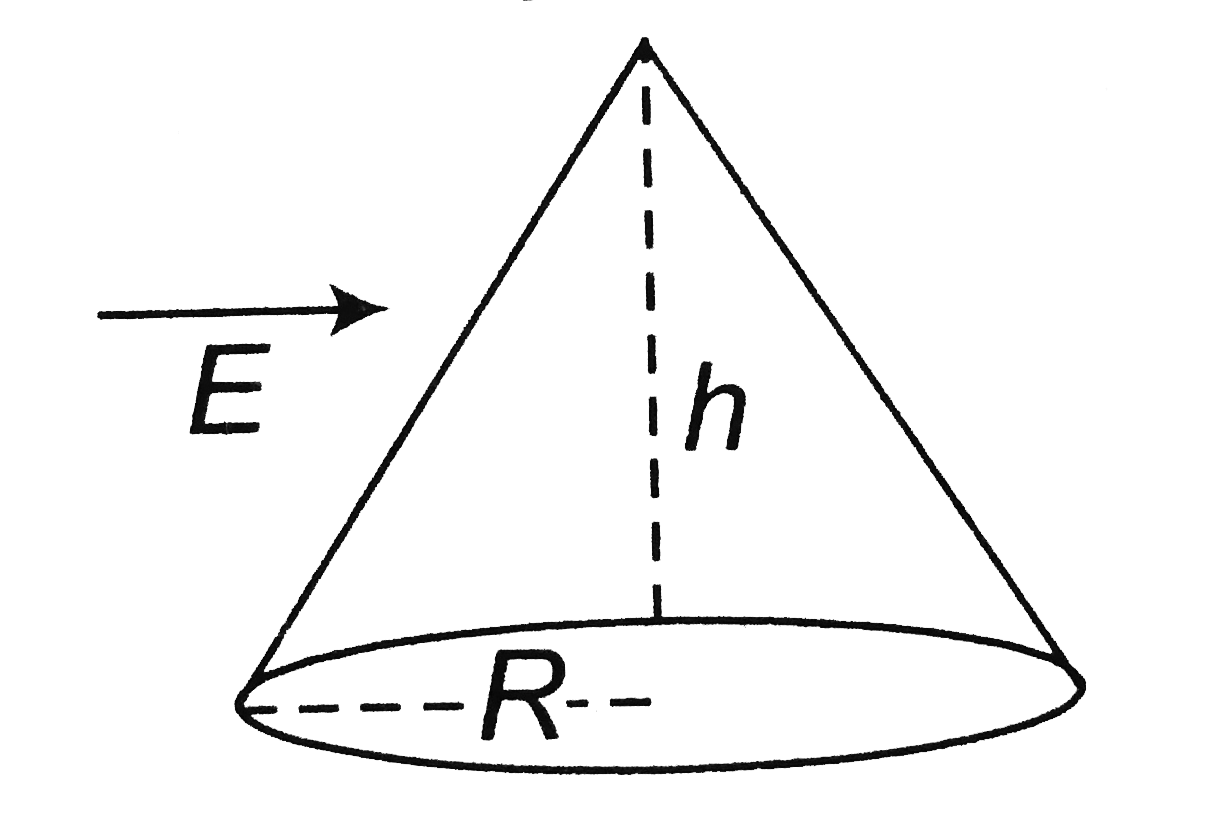 AEπR2BERhCEhR2DEh2
AEπR2BERhCEhR2DEh2
If a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is E B
View SolutionA hemispherical body is placed in a uniform electric field E. What is the flux linked with the curved surface if the field is (a) parallel to base of the body , (b) perpendicular to base of the body and (c) perpendicular to the curved surface at every points as in figure.

View SolutionA cube of side l is p laced in a uniform field E, where E=Eˆi. The net electric flux through the cube is
View SolutionA cube of side l is placed in a uniform field E, where E= Eˆi .The net electric flux through the cube is
View SolutionThe electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
View Solution