A cube of side l is p laced in a uniform field E, where E=Eˆi. The net electric flux through the cube is
zero
l2E
4l2E
6l2E
The correct Answer is:A
To find the net electric flux through a cube placed in a uniform electric field E=E^i, we can follow these steps:
Step 1: Understand the Geometry of the Cube
Consider a cube of side length l. The cube has six faces, and we need to analyze the orientation of these faces with respect to the electric field direction.
Step 2: Identify the Direction of the Electric Field
The electric field is given as E=E^i, which means it is directed along the positive x-axis.
Step 3: Determine the Area Vectors of the Cube Faces
Each face of the cube has an area A=l2. The area vectors for the faces of the cube are as follows:
- Face 1 (front face): Area vector A1=l2^i
- Face 2 (back face): Area vector A2=−l2^i
- Face 3 (left face): Area vector A3=−l2^j
- Face 4 (right face): Area vector A4=l2^j
- Face 5 (top face): Area vector A5=l2^k
- Face 6 (bottom face): Area vector A6=−l2^k
Step 4: Calculate the Electric Flux Through Each Face
The electric flux Φ through a surface is given by the formula:
Φ=E⋅A=EAcosθ
where θ is the angle between the electric field vector and the area vector.
- For Face 1 (front face):
Φ1=E⋅(l2^i)=El2⋅1=El2
- For Face 2 (back face):
Φ2=E⋅(−l2^i)=El2⋅(−1)=−El2
- For Face 3 (left face):
Φ3=E⋅(−l2^j)=El2⋅0=0
- For Face 4 (right face):
Φ4=E⋅(l2^j)=El2⋅0=0
- For Face 5 (top face):
Φ5=E⋅(l2^k)=El2⋅0=0
- For Face 6 (bottom face):
Φ6=E⋅(−l2^k)=El2⋅0=0
Step 5: Sum the Electric Fluxes
Now, we can find the total electric flux through the cube by summing the fluxes through all six faces:
Φnet=Φ1+Φ2+Φ3+Φ4+Φ5+Φ6
Substituting the values we calculated:
Φnet=El2−El2+0+0+0+0=0
Conclusion
The net electric flux through the cube is:
Φnet=0
Consider a cube of side length l. The cube has six faces, and we need to analyze the orientation of these faces with respect to the electric field direction.
The electric field is given as E=E^i, which means it is directed along the positive x-axis.
Each face of the cube has an area A=l2. The area vectors for the faces of the cube are as follows:
- Face 1 (front face): Area vector A1=l2^i
- Face 2 (back face): Area vector A2=−l2^i
- Face 3 (left face): Area vector A3=−l2^j
- Face 4 (right face): Area vector A4=l2^j
- Face 5 (top face): Area vector A5=l2^k
- Face 6 (bottom face): Area vector A6=−l2^k
The electric flux Φ through a surface is given by the formula:
Φ=E⋅A=EAcosθ
where θ is the angle between the electric field vector and the area vector.
Φ1=E⋅(l2^i)=El2⋅1=El2
Φ2=E⋅(−l2^i)=El2⋅(−1)=−El2
Φ3=E⋅(−l2^j)=El2⋅0=0
Φ4=E⋅(l2^j)=El2⋅0=0
Φ5=E⋅(l2^k)=El2⋅0=0
Φ6=E⋅(−l2^k)=El2⋅0=0
Now, we can find the total electric flux through the cube by summing the fluxes through all six faces:
Φnet=Φ1+Φ2+Φ3+Φ4+Φ5+Φ6
Substituting the values we calculated:
Φnet=El2−El2+0+0+0+0=0
The net electric flux through the cube is:
Φnet=0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -3
50 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (C.W.)
39 Videos
- DUAL NATUREBOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)
17 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)
23 Videos
Similar Questions
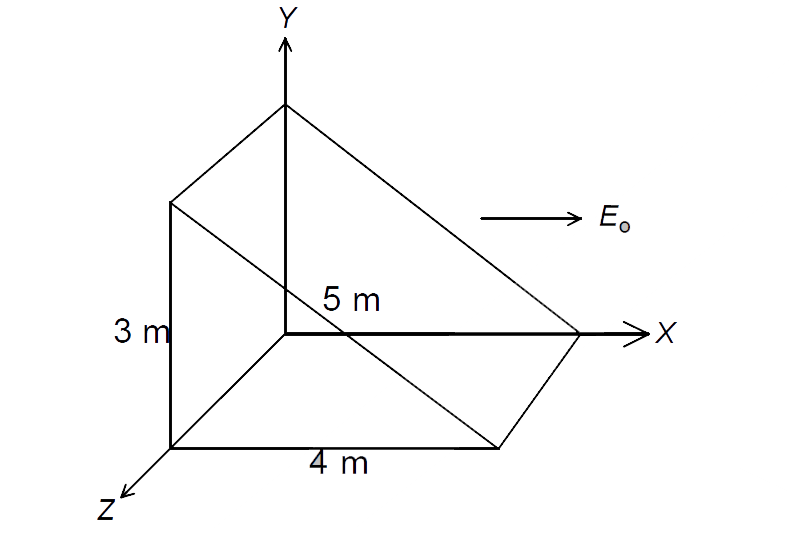
The wedge-shaped surface in figure is in a region of uniform electric field E0 along x axis. The net electric flux for the entire closed surface is -
View SolutionAn electric dipole of dipole moment →p consists of point charges +q and -q separated by a distance '2a' apart. Deduce the expression for the electric field →E due to the dipole on its axial line in term of the dipole moment →p. Hence show that in the limit r>>a,→E=2→p4π∈0r3
(b) Given the electric field in the region →E=2xˆi Find the net electric flux through the cube and the charge enclosed by it.
View Solution
Knowledge Check
A cube of side l is placed in a uniform field E, where E= Eˆi .The net electric flux through the cube is
AzeroBl2EC4l2ED6l2EA hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
Aπr2EB2πrE2C4πr2ED4πrE2A cube of side L encloses a charge Q at its centre , electric flux through the cube is
AQ∈0BQ6L2∈0CQL2∈0Dzero
An electric field given →E=4.0ˆi−3.0(y2+2.0)j pierces a Gaussian cube of edge length 2.0 m and positioned as shown in the figure. (The magnitude E is in newtons per coulomb and the position z is in meters.) what is the electric flux through the (a) top face, (b) bottom face, (c) left face , (b) bottom facem (c) left face, and (d) back face ? (e) what is the net electric flux through the cube ?

View SolutionA cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
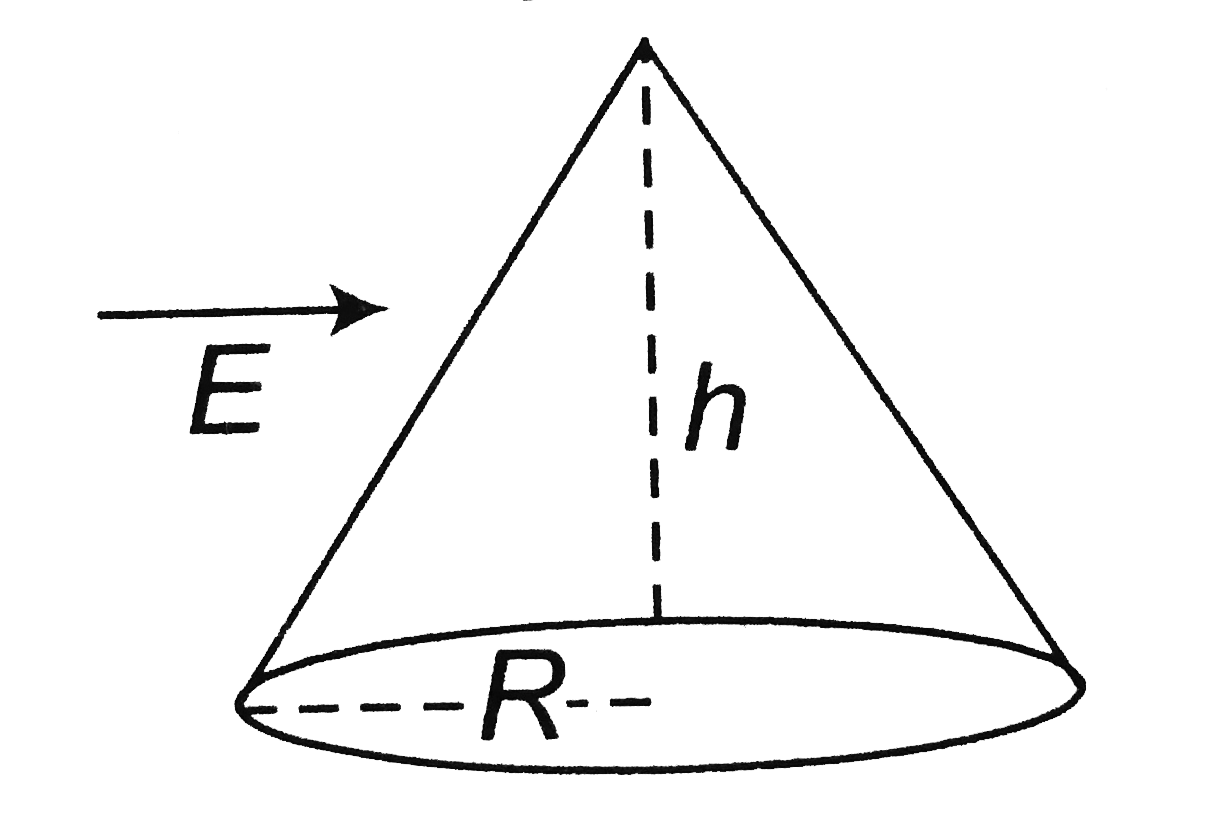
View SolutionIn figure, a cone lies in a uniform electric field E. Determine the electric flux entering the cone.
 .
.
View SolutionA very small sphere having a charge q, uniformly distributed throughout its volume, is placed at the vertex of a cube of side a. The electric flux through the cube is
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View Solution
