Consider two concentric spherical surface S1 with radius a and S2 with radius 2a ,both centred on the origin. There is a charge +q at the origin, and no other charges.Compare the flux ϕ1 through S1 with the flux ϕ2 through S2.
ϕ1=4ϕ2
ϕ1=2ϕ2
ϕ1=ϕ2
ph1=ϕ2/2
The correct Answer is:C
Flux through both will be same as net charge enclosed by both is same.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -3
50 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (C.W.)
39 Videos
- DUAL NATUREBOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)
17 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)
23 Videos
Similar Questions
A sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ration of electric flux through S1andS2,
View SolutionS1andS2 are two concentric sphere enclosing charges 2Q and 3Q respectively as shown in the figure. What is the ratio of the electric flux through S1andS2?
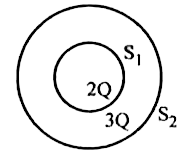
View Solution
Knowledge Check
Conside r two concentric spherical surface S1 with radius a and S2 with radius 2a ,both centred on the origin. There is a charge +q at the origin, and no other charges.Compare the flux ϕ through S1withthefluxphi_(2)throughS_(2).
Aϕ1=4ϕ2Bϕ1=2ϕ2Cϕ1=ϕ2Dϕ1=ϕ2/2Consider two concentric spherical surfaces S1 with radius a and S2 with radius 2a, both centered at the origin. There is a charge +q at the origin and there are no other charges. Compare the flux ϕ1 through S1 with the flux ϕ2 through S2.
Aϕ1=4ϕ2Bϕ1=2ϕ2Cϕ1=ϕ2Dϕ1=ϕ2/2Two concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
Aq1=4πε0(ϕ1−ϕ2a2−a1)a1a2Bq1=4πε0(ϕ1+ϕ2a2+a1)a1a2Cq1=πε0(ϕ1−ϕ2a2+a1)a1a2Dq1=2πε0(ϕ1+ϕ2a2−a1)a1a2
A conducting sphere S1 intersects a closed surface S2 as shown in the figure.A positive charge q is placed at a point P .What is the value of electric flux through the surface S2 ? q P
View SolutionIf the radius of the Gaussion surface enclosing a charge q is halved, how does the electric flux through the Gaussion surface change?
View SolutionA sphere S1 of radius r enclose a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additioanl charges between S1andS2 find the ratio of electric flux through S1andS2
View SolutionThe ratio of ψε passing through the surfaces S1 and S2 is-
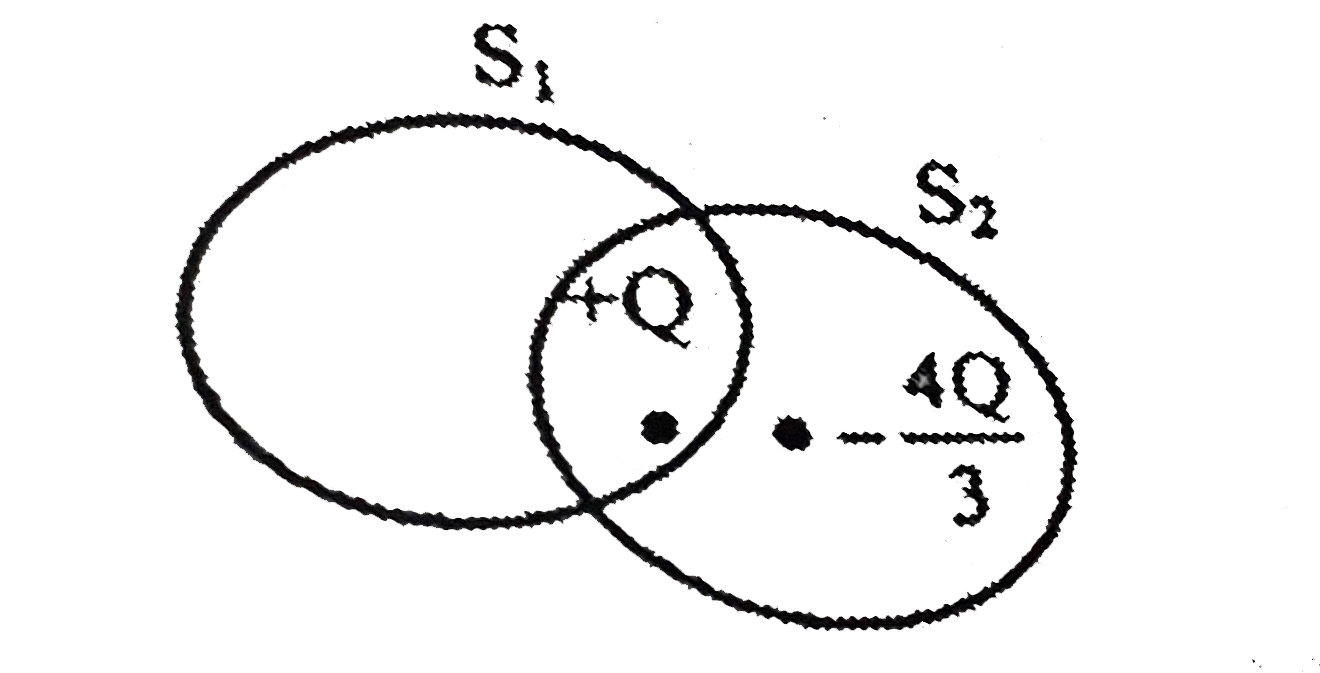
View SolutionA point charge Q is surrounded by two concentric spherical surfaces of radii R and 2R, respectively. A point charge is at the common centre. If f1 and f2 be the total electric flux over surfaces (1) and (2), then f1/f2 will be

View Solution
