Column-I show vector diagram relating three vectors →a,→b and →c. Match the vector equation in column -II, with vector diagram in column-I:
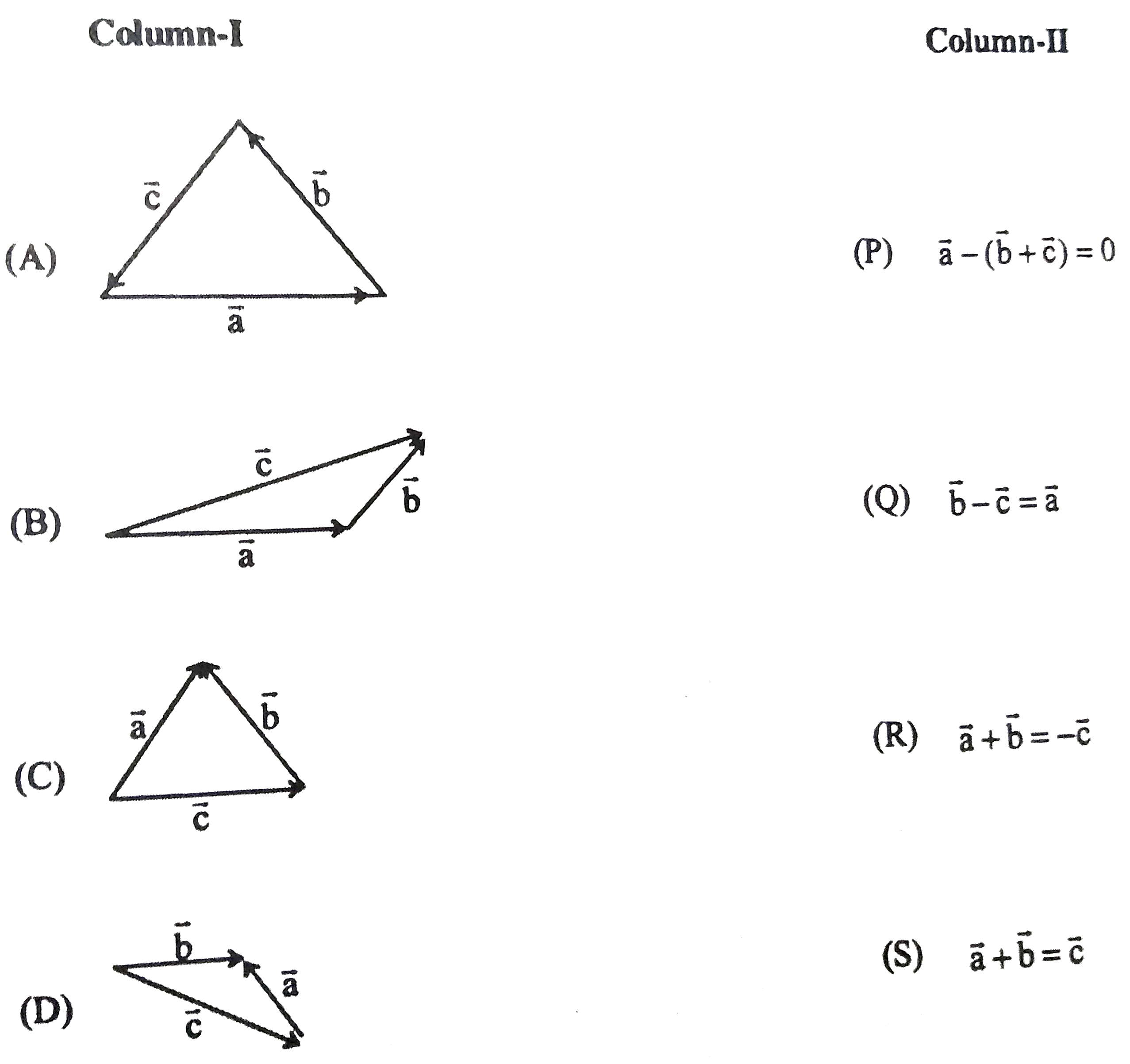
The correct Answer is:(A)-(R);(B)-(S);(C)-(P);(D)-(Q)
Step by step video, text & image solution for Column-I show vector diagram relating three vectors veca, vecb " and " vecc. Match the vector equation in column -II, with vector diagram in column-I: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-2) Single Correct Type Questions.
Explore 17 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-2) Multiple Correct Type Questions.
Explore 7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-1) ParagraphType Questions.
Explore 2 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHS
Explore 18 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Previous Year Questions)
Explore 7 Videos
Similar Questions
Knowledge Check
For any three vectors →a,→b,→c the vector (→b×→c)×→a equals
A(→a.→b)→c−(→b.→c)→aB(→a.→b)→c−(→a.→c)→bC(→b.→a)→c−(→c.→a)→bDnone of theseThree vectors →a,→b and →c satisfy the relation →a.→b=0 and →a.→c=0. The vector →a is parallel to
A→bB→C must be less than ∣∣→A−→B∣∣C→b.→cD→b×→cIf →A,→B and →C are coplanar vectors, then
A(→A.→B)×→C=0B(→A×→B)→C=0C(→A.→B)→C=0Dall the above are true
Given below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
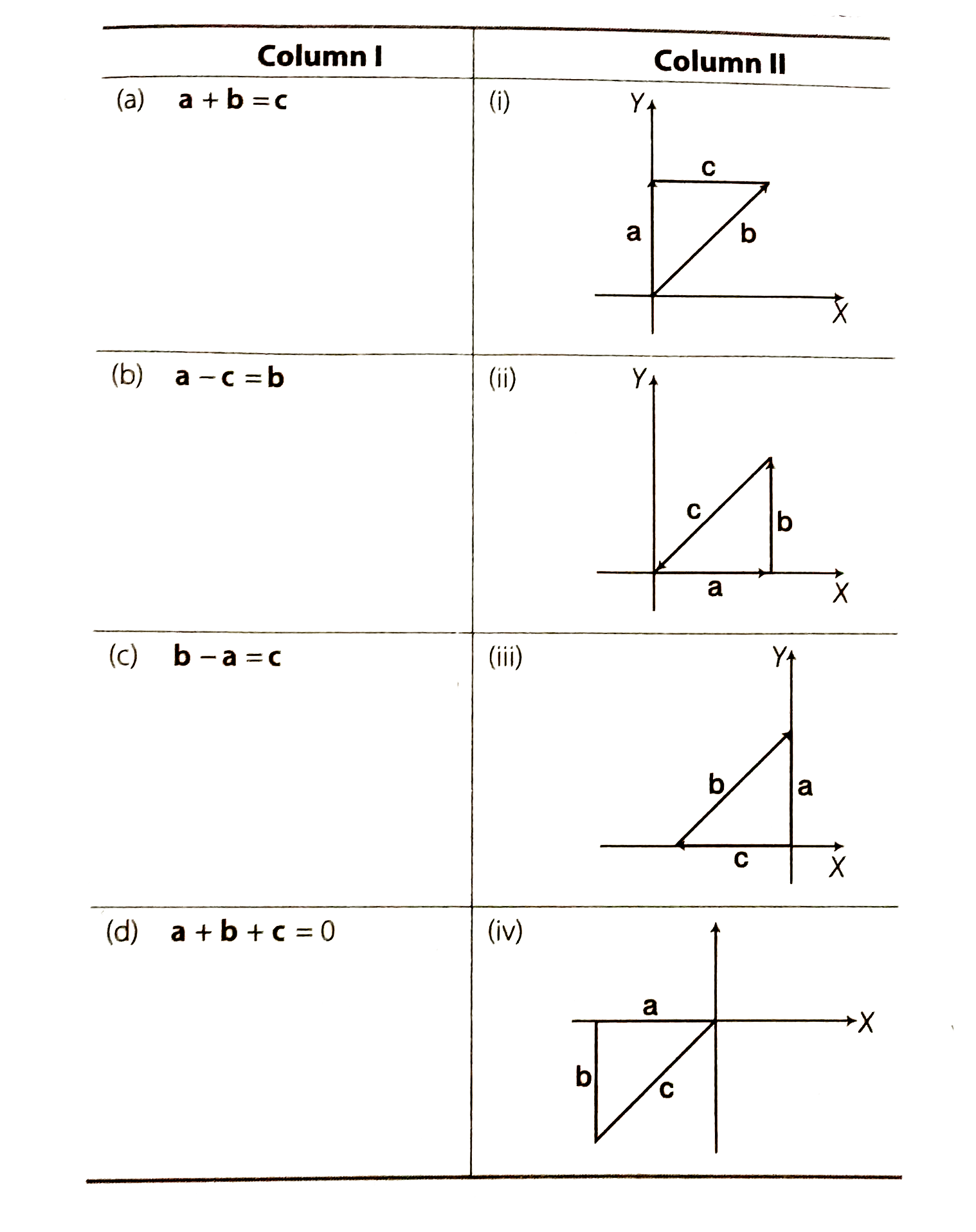
View SolutionThree vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
View Solutionif →a,→b,→c are three vectors such that →a+→b+→c=→0 then
View SolutionThe vector sum of three vectors→A,→B and →C is zero . If ˆi and ˆj are the unit vectores in the vectors in the directions of →A and →B respectively , them :
View SolutionFor any three vectors →a,→b,→c the value of [→a−→b→b−→c→c−→a], is
View Solution

