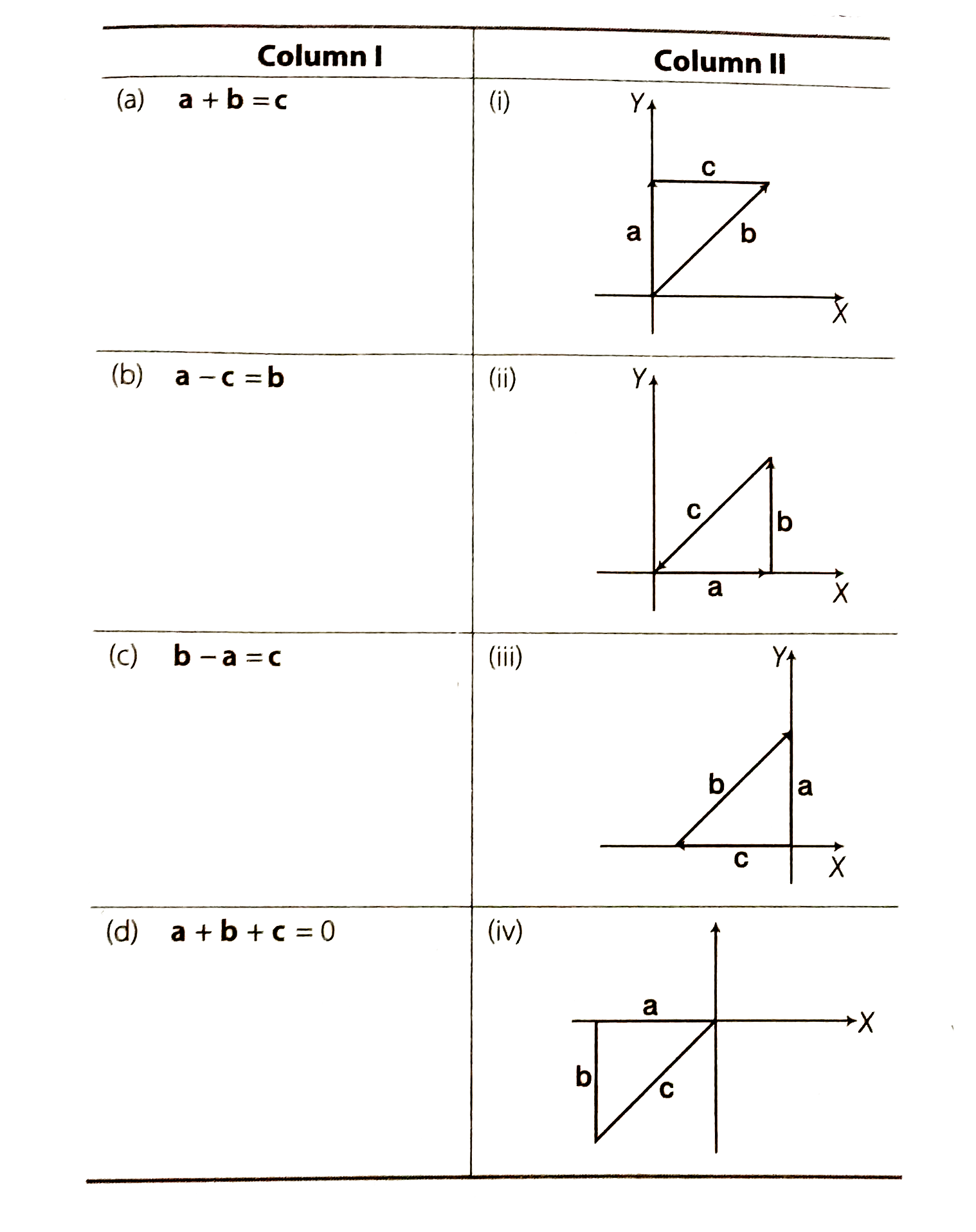
Given below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
Video Solution
Text Solution
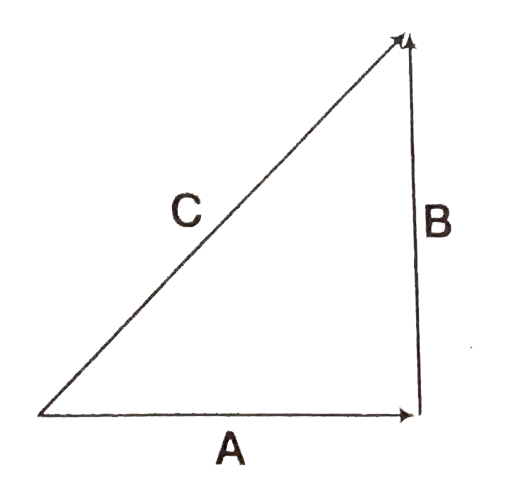
Consider the adjacent diagram in which vectors A and B are corrected by head and tail .
Resultant vector C= A+B
(a) from (iv) it is clear that c=a+b
(b) from (iii) c+b=a⇒a−c=b
(c) from (i) b=a+c⇒b−a=c
(d) from (ii) −c=a+b⇒a+b+c=0
|
Topper's Solved these Questions
Similar Questions
Given below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.

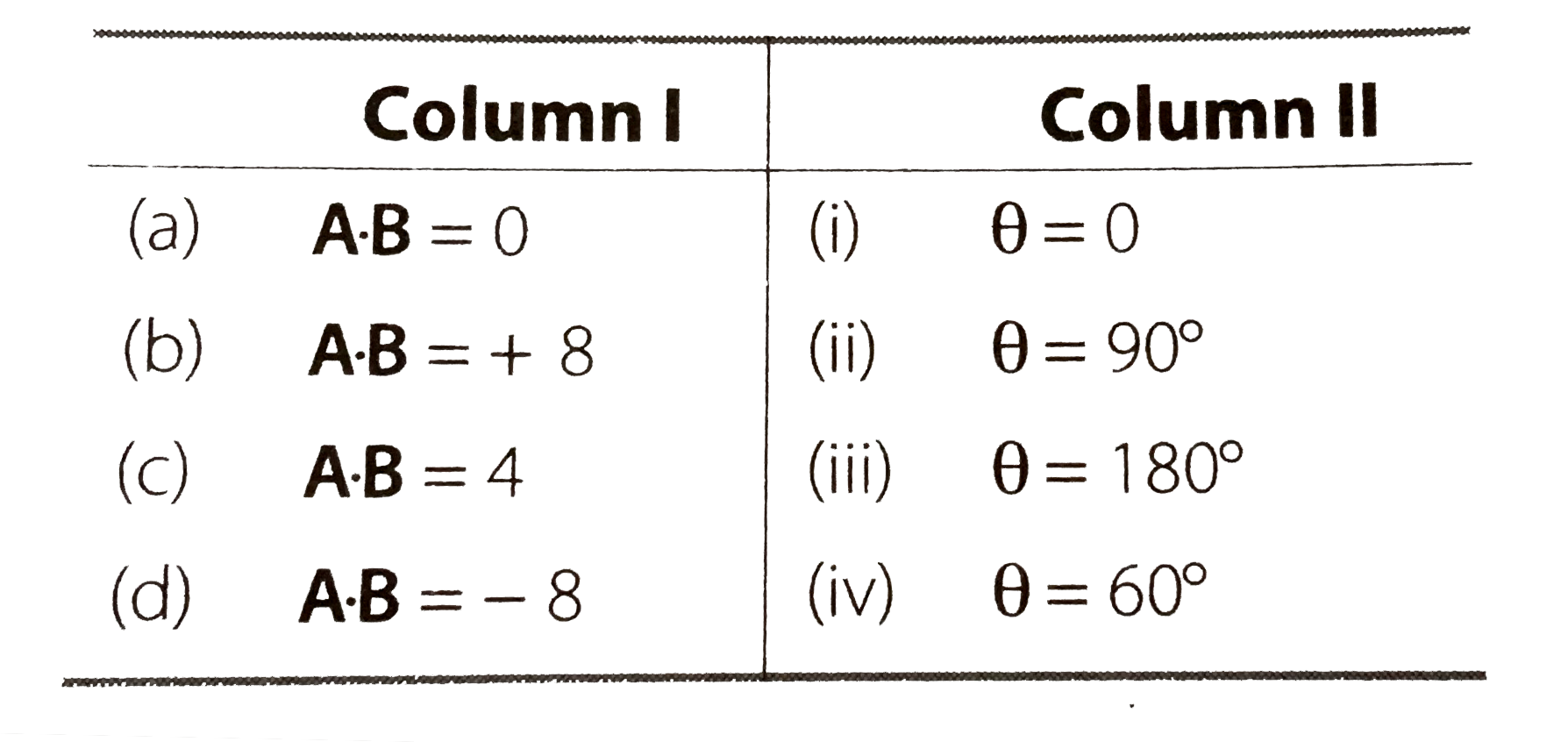
View SolutionIf |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
View Solution
Knowledge Check
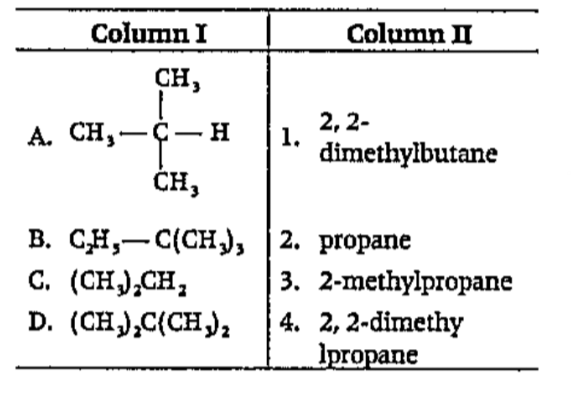
Match the Column I and Column II.,B
 AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-qMatch between column I and column-II and choose the correct answer ?
 AA-iv, B-iii, C-ii, D-iBA-iv, B-ii, C-i, D-iiiCA-i, B-ii, C-iii, D-ivDA-iii, B-iv, C-ii, D-i
AA-iv, B-iii, C-ii, D-iBA-iv, B-ii, C-i, D-iiiCA-i, B-ii, C-iii, D-ivDA-iii, B-iv, C-ii, D-iMatch the Column I with Column II and select correct answer given codes.
 A
A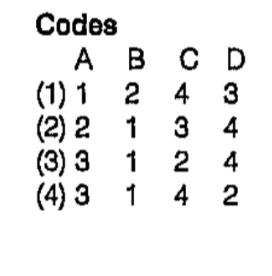 B
B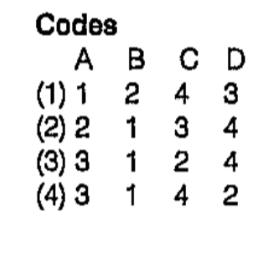 C
C D
D
Match the items given in Column I and Column II.

View SolutionMatch the items given in Column I and Column II.
View SolutionMatch the statements given h, column I to the related description given In column II

View SolutionMatch the items given in Column I with those in Column II.

The correct option is
View SolutionMatch the items given in Column I with those in Column II.

The correct option is
View Solution

