Show a vector →a at angle θ as shown in the figure column-II. Shows its unit vector representation.
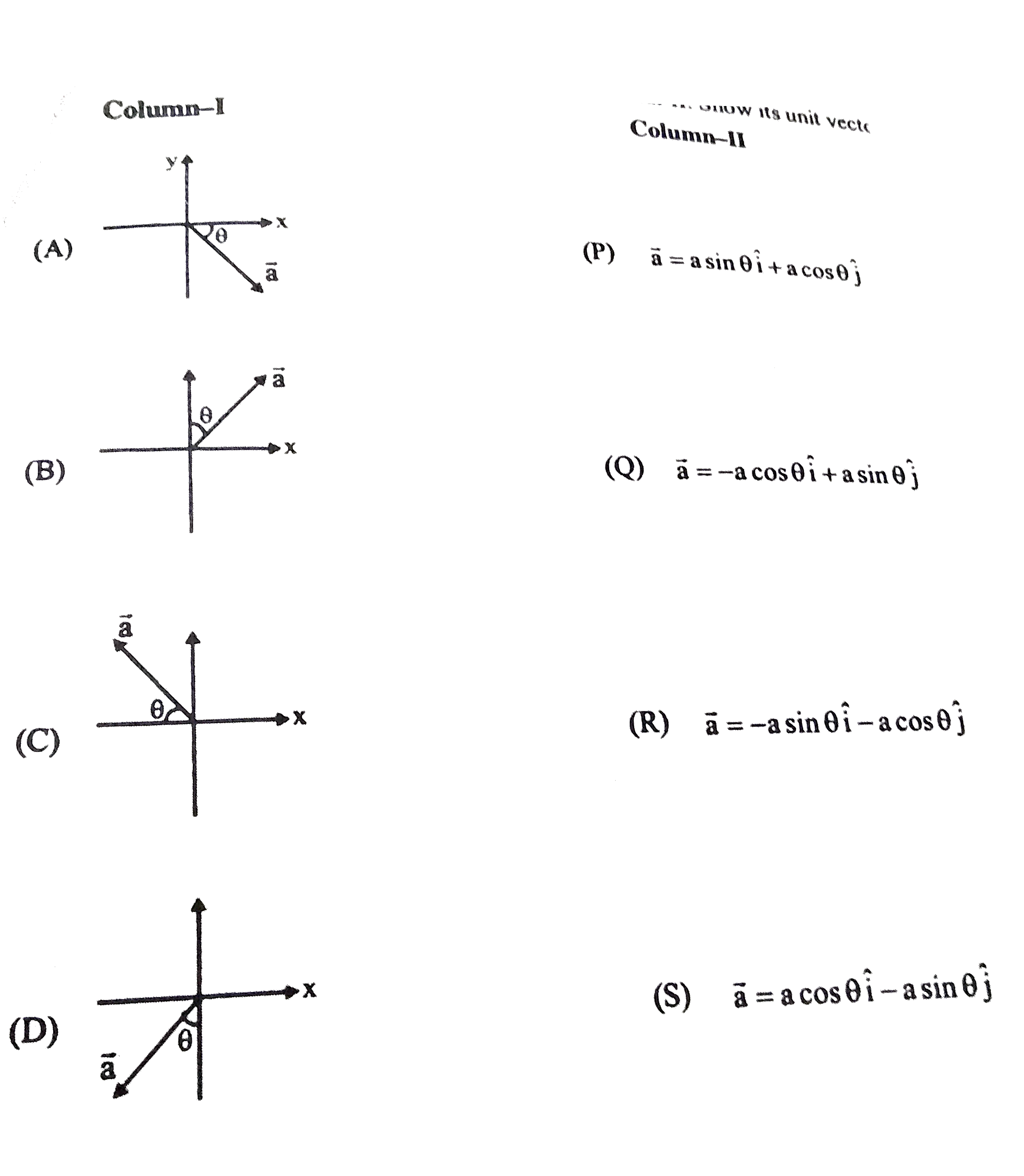
The correct Answer is:(A)-(S);(B)-(P);(C)-(Q);(D)-(R)
Step by step video, text & image solution for Show a vector veca at angle theta as shown in the figure column-II. Shows its unit vector representation. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-2) Single Correct Type Questions.
Explore 17 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-2) Multiple Correct Type Questions.
Explore 7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (O-1) ParagraphType Questions.
Explore 2 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHS
Explore 18 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Previous Year Questions)
Explore 7 Videos
Similar Questions
Knowledge Check
A vector →A is rotated through angle θ about its tail. Change of position vector of its tip of is:
AAsinθB2Acos.θ2C2Asin.θ2DAcosθIf →a and →b are two unit vectors inclined at an angle θ such that |a+b|,1, then θ<π3 b. θ>2π3 c. π3<θ<2π3 d. 2π3<θ<π
Aπ3Bπ4Cπ2D2π3<θ<πIf a and b are unit vectors and θ is the angle between them, then a+b is a unit vector if θ equals
A2π3Bπ3Cπ2Dπ4
The unit vector parallel to vecA is
View SolutionIf two vectors →A and →B are at an angle θ≠0∘, then
View SolutionIf a and b are unit vectors and θ is the angle between them then a−b will be a unit vector if
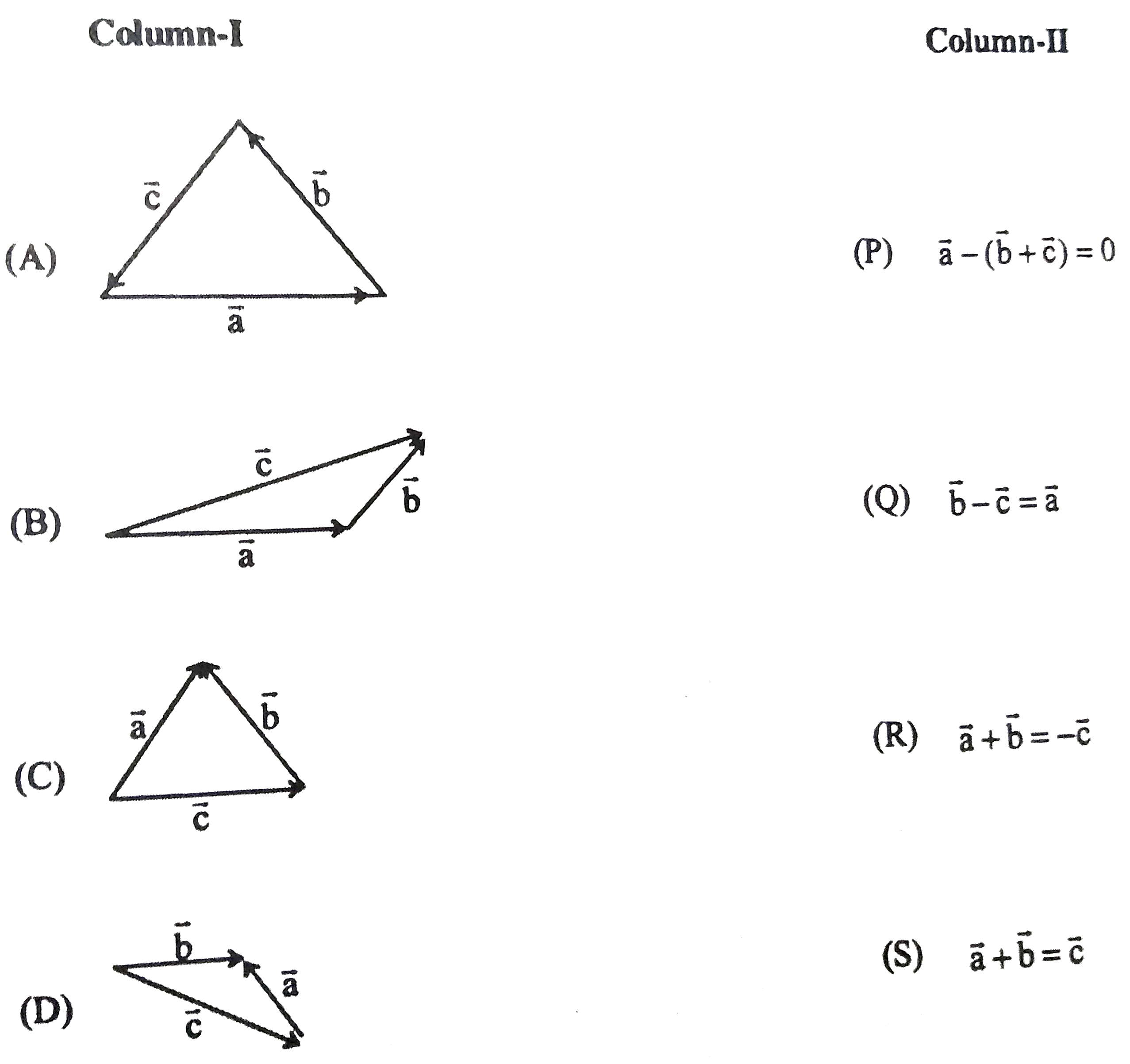
View SolutionColumn-I show vector diagram relating three vectors →a,→b and →c. Match the vector equation in column -II, with vector diagram in column-I:
View SolutionIF a unit vector →a makes angles π4andπ3 with x-axis and y-axis respectively and an acute angle theta with z-axis, then find theta and the (scalar and vector) coponents of →a along the axes.
View Solution



