A capacitor is made of two circular plates of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
Assuming initially the disc is in touch with the bottom plate, so the entire plate is a equipotential the electric field on the disc, when potential difference V is applied across it, given by ltBrgt E=Vd
Let charge q' is transferred to the disc during the process,
therefore by gauss' theorem
∴q'=−ε0Vdπr2
Since, gauss theorem states that ϕ=qε0 or q=ε0ϕ
=εEA=ε0VdA
The force acting on the disc is
−Vd×q'=ε0V2d2πr2
If the disc is to be lifted then,
ε0V2d2πr2=mg⇒V=√mgd2πε0r2
this is the required expression.
Topper's Solved these Questions
Similar Questions
A capcitor is made of two circular paltes of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc si m.
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View Solution
Knowledge Check
A capacitor made of two circular plates each of radius 12 cm and separated by 5 mm. The capacitor is being charged by an external source. The charging current is constant and equal to 0.15 A. The capacitance of the parallel plate capacitor is
 A40 pFB45 pFC70 pFD80 pF
A40 pFB45 pFC70 pFD80 pFThe two metallic plates of radius r are placed at a distance d apart and its capacity is C. If a plate of radius r/2 and thickness d of dielectric constant 6 is placed between the plates of the condenser, then its capacity will be
A7C/3B3C/7C7C/3D9C/4The radius of gyration of a uniform circular disc of radius R, about any diameter of the disc is
AK=RBK=R/2CK=2RDnone of these
A circular disc is of mass M and radius r. From it a circualr piece is cut out with a radius of the disc as its diameter. Find the moment of inertia of the remainder about the axix of the disc
View Solution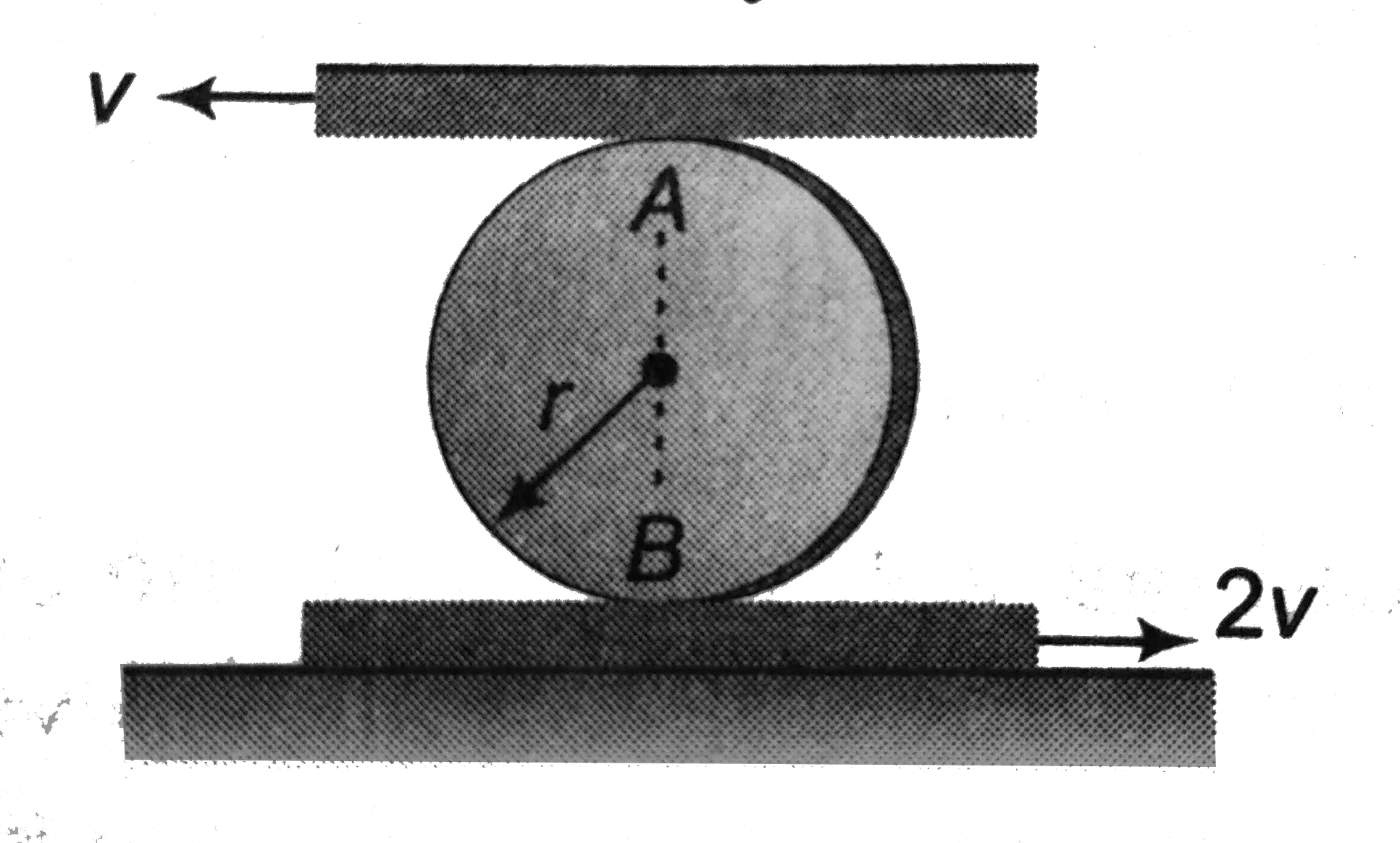
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionFrom a circular disc of radius R, another disc of diameter R is removed. Locate c.m. of the remaining portion.

View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

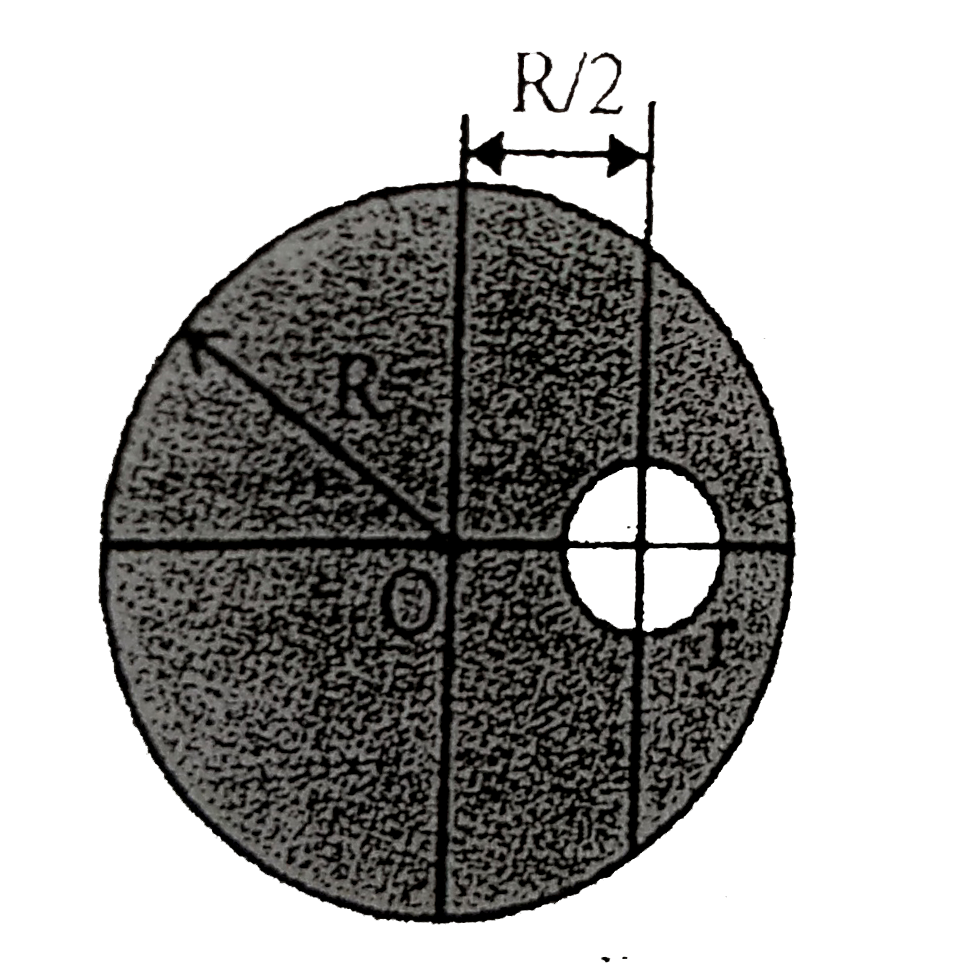
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
View Solution

