Find the equatio of the equipotentials for an infinite cylinder of radius r0 carrying charge of linear density λ.
let the field lines must be radically outward. Draw a cylinderical gaussian surface of radius r and length l. then, applying gauss' theorem
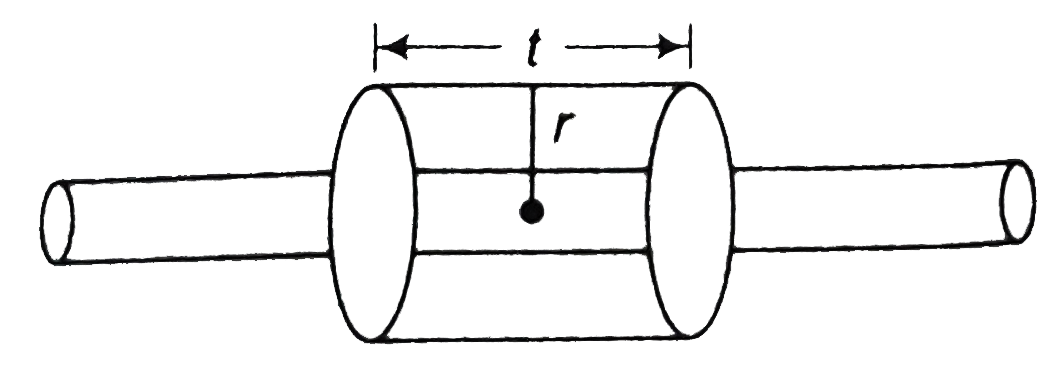
∫E.dS=1ε0λl
or Er2πrl=1ε0λl⇒Er=λ2πε0r
Hence, if r0 is the radius, V(r)−V(r0)=−∫rr0E.dl=λ2πε0ln(r0)r
Since, ∫rr0λ2πε0rdr=λ2πε0∫rr0dr=λ2πε0ln(r)r0
For a given V,
ln(r)r0=−2πε0λ[V(r)−V(r0)]
⇒r=r0e−2πε0Vr0/λe+2πε0V(r)/λ
r=r0e−2πε0[V(r)−V(r0)]/λ.
The equipotential surfaces are cylinders. of radius.
Topper's Solved these Questions
Similar Questions
Find the equatio of the equipotentials for an infinite cylinder of radius r0 carrying charge of linear density λ.
View SolutionFind the magntiude and diraction of the magnitude induction vector B
(a) of an infinite palne carrying a current of linear density I, the vector i is the same at all points of the plane,
(b) of two parallel infinite planes carrying currents of linear densities a dn -1, the vectors i and −i are cohnstant at all points of the corresponding planes.
View Solution
Knowledge Check
A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
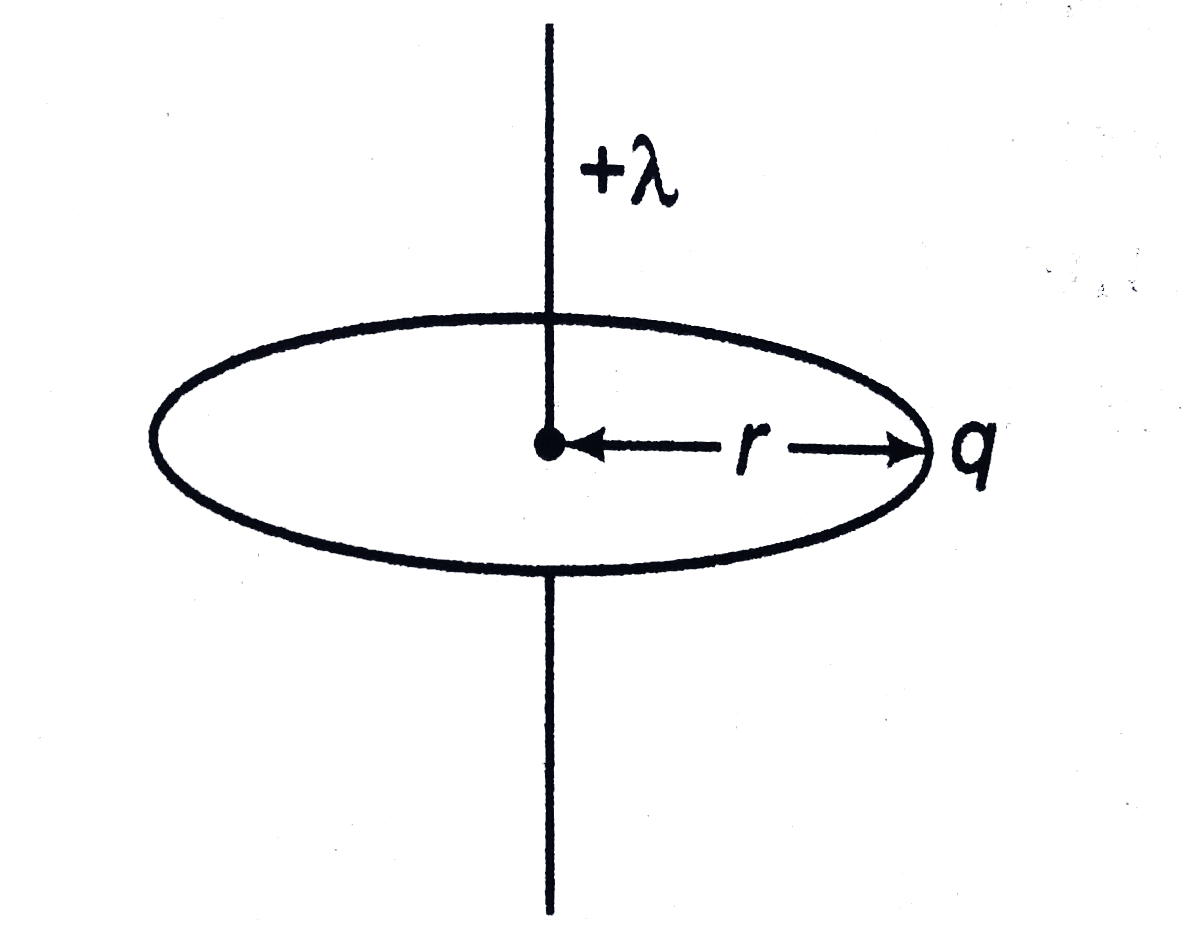 where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλq
where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλqFind ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1
Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionDraw the electric field vs distance (from the centre ) graph for (i) a long charged rod having linear charge density λ>0 (ii) spherical shell of radius R and charge Q>0 .
View SolutionFind the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = λ).
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View Solution

