An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 100N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m.ifg =10 ms^(-2), what is the speed of just before it touches the spring? 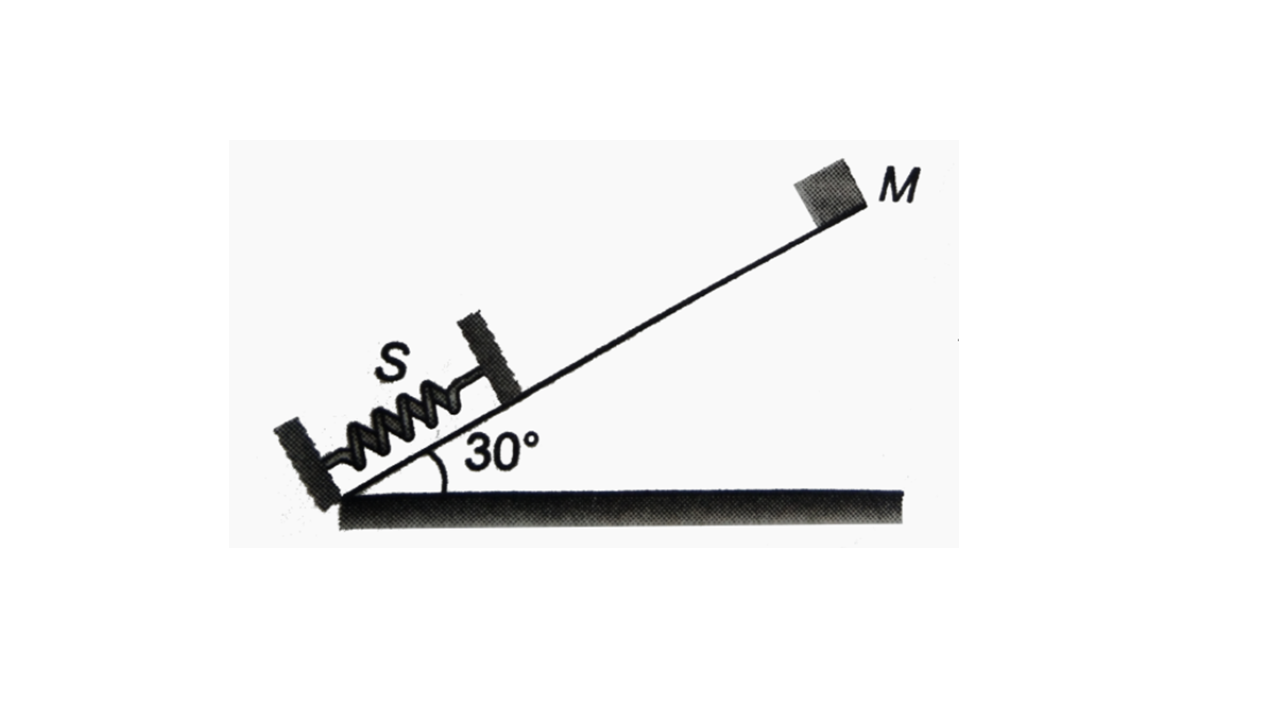 .
.
(a) Let total distance moved by the block is
S=(l+2)m,
where l is the distance moved by the block before touching the spring.
Now, work done by gravity on the block is
Wg=mgS sinθ=10×10×Ssin30J
⇒Wg=50SJ ...(1)
Work done by spring on the block is , Ws=12kx2
Here, K=100N/m and x=2m
⇒Ws=12×100×4J⇒Ws=200J ...(2)
Total work done W=Wg+Ws
⇒W=(50S−200)J
Since change in K.E. of the block is zero.
as W=ΔK.E.
⇒50S−200=0
⇒S=4m

(b) As S=l+2⇒l=S−2=2m
Work done by gravity over this path length is
Wg=mg×2sinθ=10×10×2×12=100J [∴Wg=ΔK.E.]
⇒100=12mv2−0⇒v2=100×210=20
⇒v=2√5m/s
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:SOLVED PROBLEMS (SUBJECTIVE )
Explore 8 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:SOLVED PROBLEMS ( OBJECTIVE)
Explore 18 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
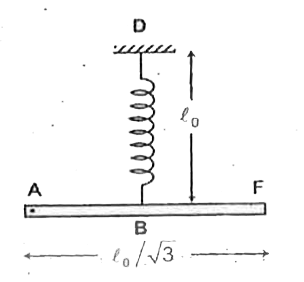
In the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionWhen a man walks on a horizontal surface with constant velocity, work done by
View Solution
A particle of mass 3m is projected from point-A with speed 3v0 as shown in figure. When the particle is at point P, it explodes in three identical particles choose the INCORRECT statement regarding the physical quantities just before and just after explosion
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.
View SolutionAn ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000 N . This same spring is placed at the bottom of a friction less inclined plane which makes an angle theta =30^@ with the horizontal. A 10 kg mass m is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by 2.0 m. the distance through which the mass moved before coming to rest is.
View SolutionAn ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000 N . This same spring is placed at the bottom of a friction less inclined plane which makes an angle theta =30^@ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2 m. if g =10 ms^(-1) , what is the speed of just before it touches the spring? .
View SolutionA block of 4kg mass starts at rest and slides a distance d down a friction less incline ( angle 30^@ ) where it runs into a spring of negligible mass. The block slides an additional 25m before it is brought to rest momentarily by compressing the spring. The force constant of the spring is 400Nm^-1 . The value of d is (take g=10ms^-2 )
View SolutionA block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionAn ideal massless spring is compressed by 1 m by a force of 100 N. The same spring is placed at the bottom of a frictionless inclined plane (theta = 30^(@)) . A 10-kg mass is released from the top of the incline and is brought to rest momentarily after compressing the spring by 2m. Through what distance does the mass slide before coming to rest ? [Hint : Apply work-energy theorem]
View SolutionAn ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?

View SolutionA block of mass sqrt2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
View Solutionद्रव्यमान 0.1 किग्रा का एक पिण्ड वेग 10 मीटर/सेकण्ड से बल नियतांक 1000 न्यूटन/मीटर वाली एक स्प्रिंग से टकराता हैं ( स्प्रिंग का दूसरा सिरा कसा हैं ) तथा स्प्रिंग को सम्पीड़ित करने के पश्चात विराम पर आ जाता हैं | स्प्रिंग का सम्पीडन होगा :
View Solution9 किलोग्राम द्रव्यमान का एक पिण्ड घर्षण रहित पृष्ठ पर4m/s के वेग से गतिशील है। यह पिण्ड एक आदर्श स्प्रिंग से टकराकर तथा उसे सम्पीडित कर विरामावस्था में आ जाती है। यदि स्प्रिंग का बल नियतांक 100 N/m हो , तो स्प्रिंग में कितना सम्पीडन होगा ?
View Solution16 kg. A block of mass moving on a frictionless horizontal plane at a velocity of 4 m / s, compresses a spring to a break state. If the force constant of the spring is 100 N / m then how compressed will the spring be
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View Solution