An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m. If g=10ms−1, what is the speed of just before it touches the spring? 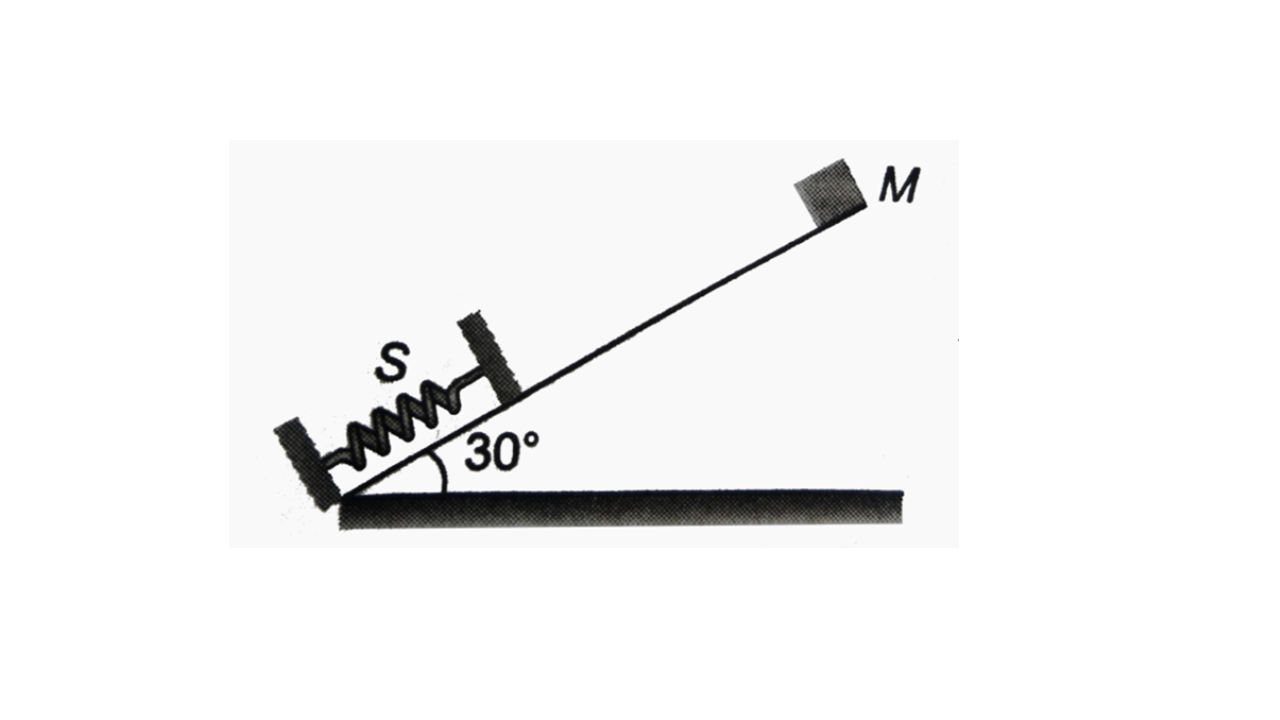 .
.
√20ms−1
√30ms−1
√10ms−1
√40ms−1
The correct Answer is:A
F=kx
∴k=Fx=1001
=100N/m
Ei=Ef
∴12×10×v2=12×100×(2)2−(10)(10)(2sin30∘)
Solving we get,
v=√20m/s
Similar Questions
An ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?

View SolutionAn ideal massless spring is compressed by 1 m by a force of 100 N. The same spring is placed at the bottom of a frictionless inclined plane (θ=30∘). A 10-kg mass is released from the top of the incline and is brought to rest momentarily after compressing the spring by 2m. Through what distance does the mass slide before coming to rest ?
[Hint : Apply work-energy theorem]
View Solution
Knowledge Check
An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A 10kg mass m is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by 2.0m. the distance through which the mass moved before coming to rest is.
A8mB6mC4mD5mWhen a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/mA block of 4kg mass starts at rest and slides a distance d down a friction less incline ( angle 30∘) where it runs into a spring of negligible mass. The block slides an additional 25m before it is brought to rest momentarily by compressing the spring. The force constant of the spring is 400Nm−1. The value of d is (take g=10ms−2)
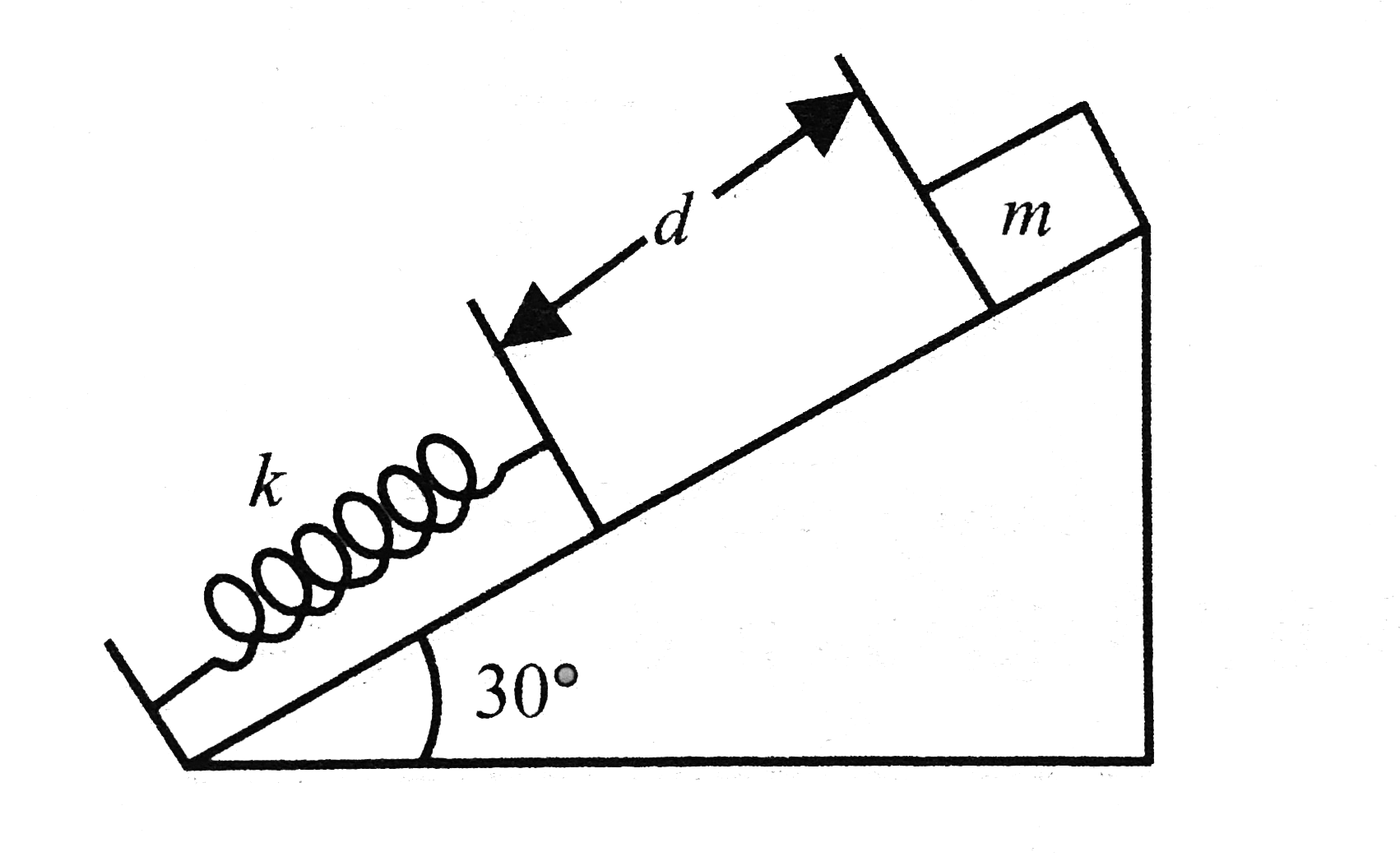 A(a) 25cmB(b) 37.5cmC(c) 62.5cmD(d) None of the above
A(a) 25cmB(b) 37.5cmC(c) 62.5cmD(d) None of the above
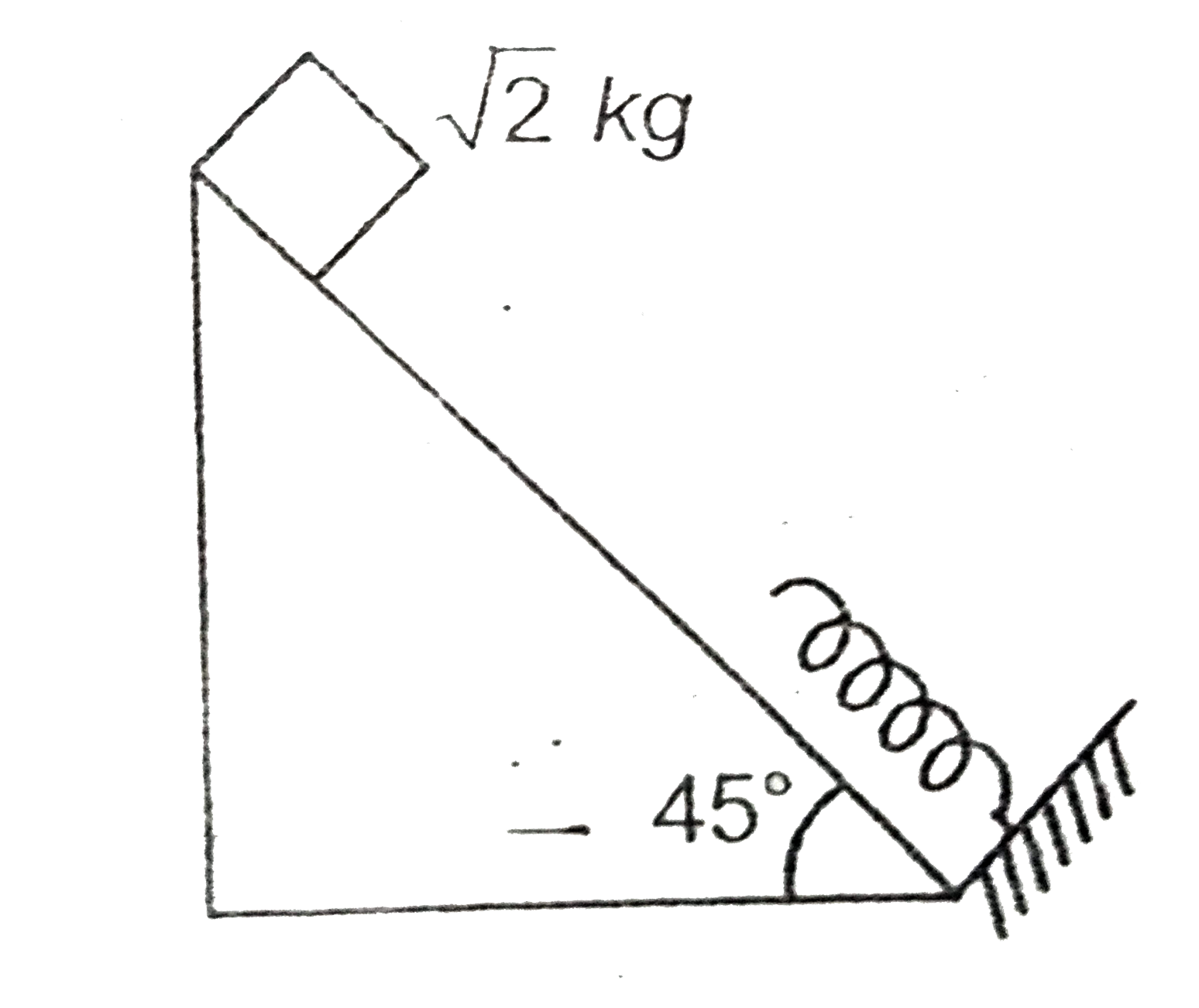
A block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionAn inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View Solution

