Two particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then

v1=v2√2
v1=v2
v2=√2v1
v2=v1√32
The correct Answer is:A
Step by step video, text & image solution for Two particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v_(1) and v_(2) as shown in the figure. It is found that they collide. Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
20 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
15 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Two particles start simulataneously from the same point and moves along two straight lines inclined at angle α, one with uniform velocity v0 and other from the rest with uniform acceleration, a0. After how much time their relative velocity is minimum and what is it equal to?
View Solution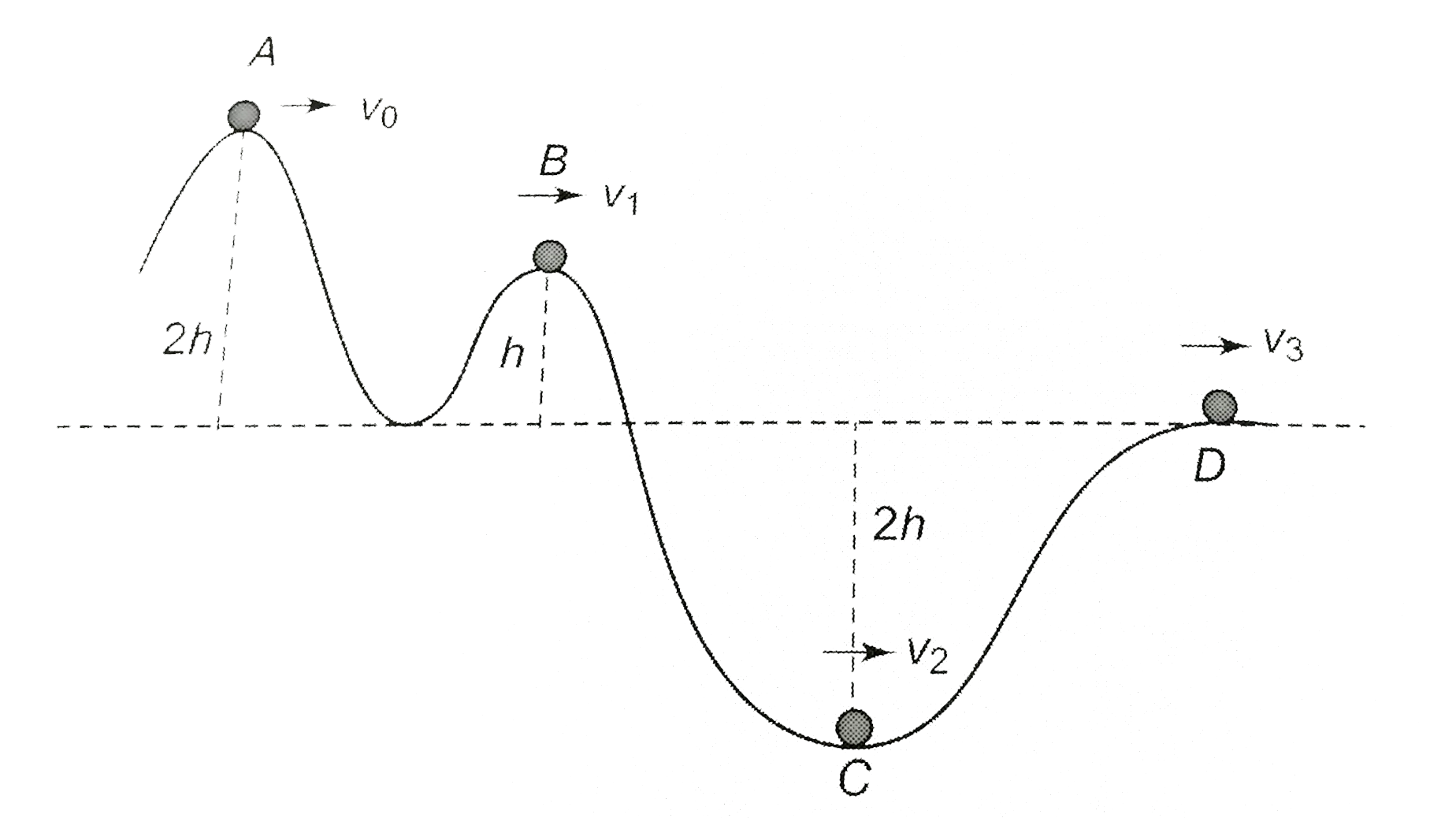
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and D
View Solution
Knowledge Check
Two particles projected vertically upward from points (0,0) and (1,0)m with uniform velocity 10m/s and vm/s respectively, as shown in the figure. It is found that they collide after time t in space. Time t is 15(√x−1). Calculate x
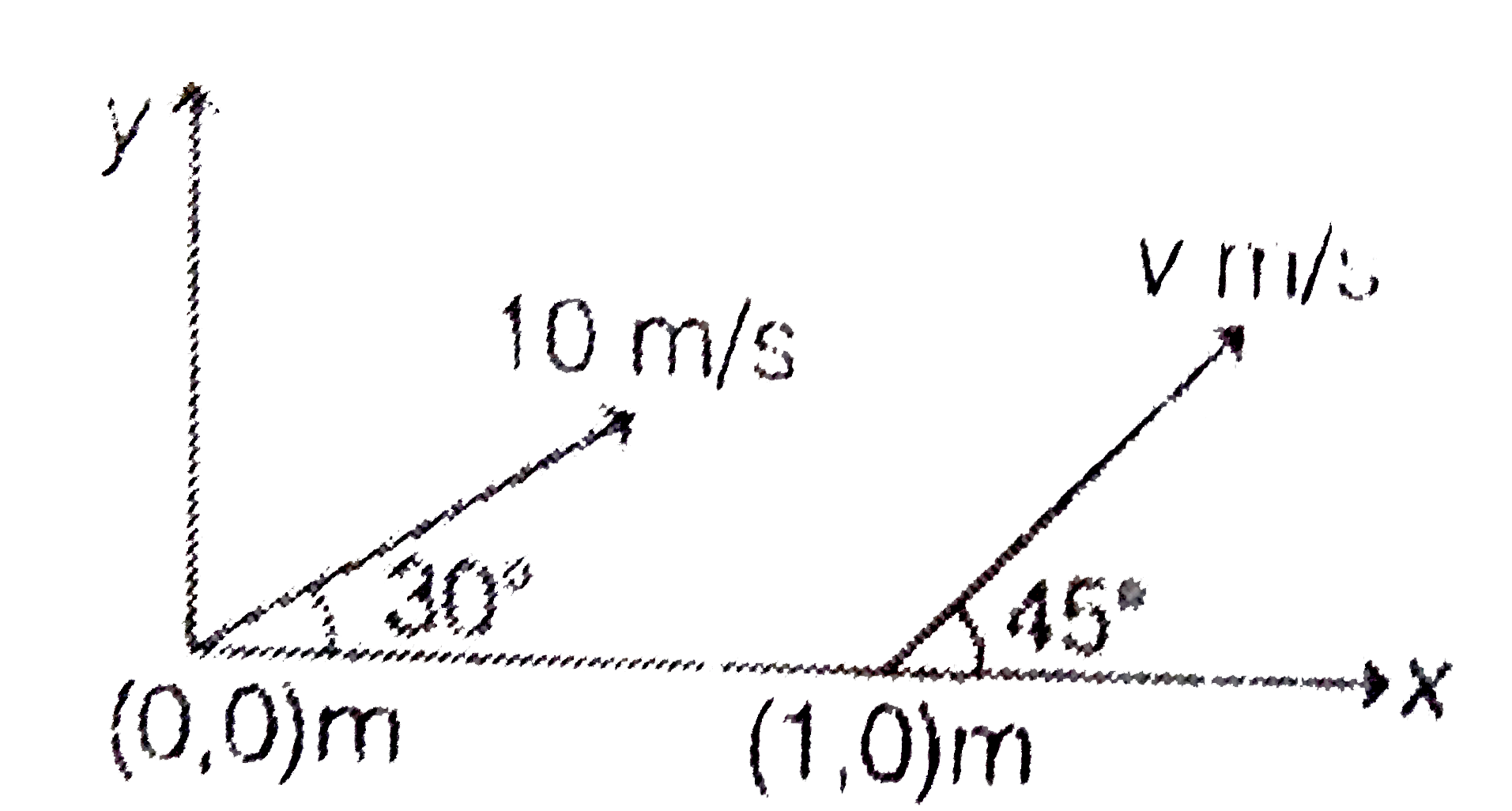 A2B3C5D8
A2B3C5D8Two particles A and B locat at (0,0) and (4,4) respectively start moving simu lataneou ly with velocities vA=−4ˆi and VB=−4ˆj:
Athe shortest distance between them is 4√2mBthe shortest distance between them first decreases and then increasesCthe distance between them increases from the beginningDthe magnitude of relative velocity of A w.r.t. B is 4m/sTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
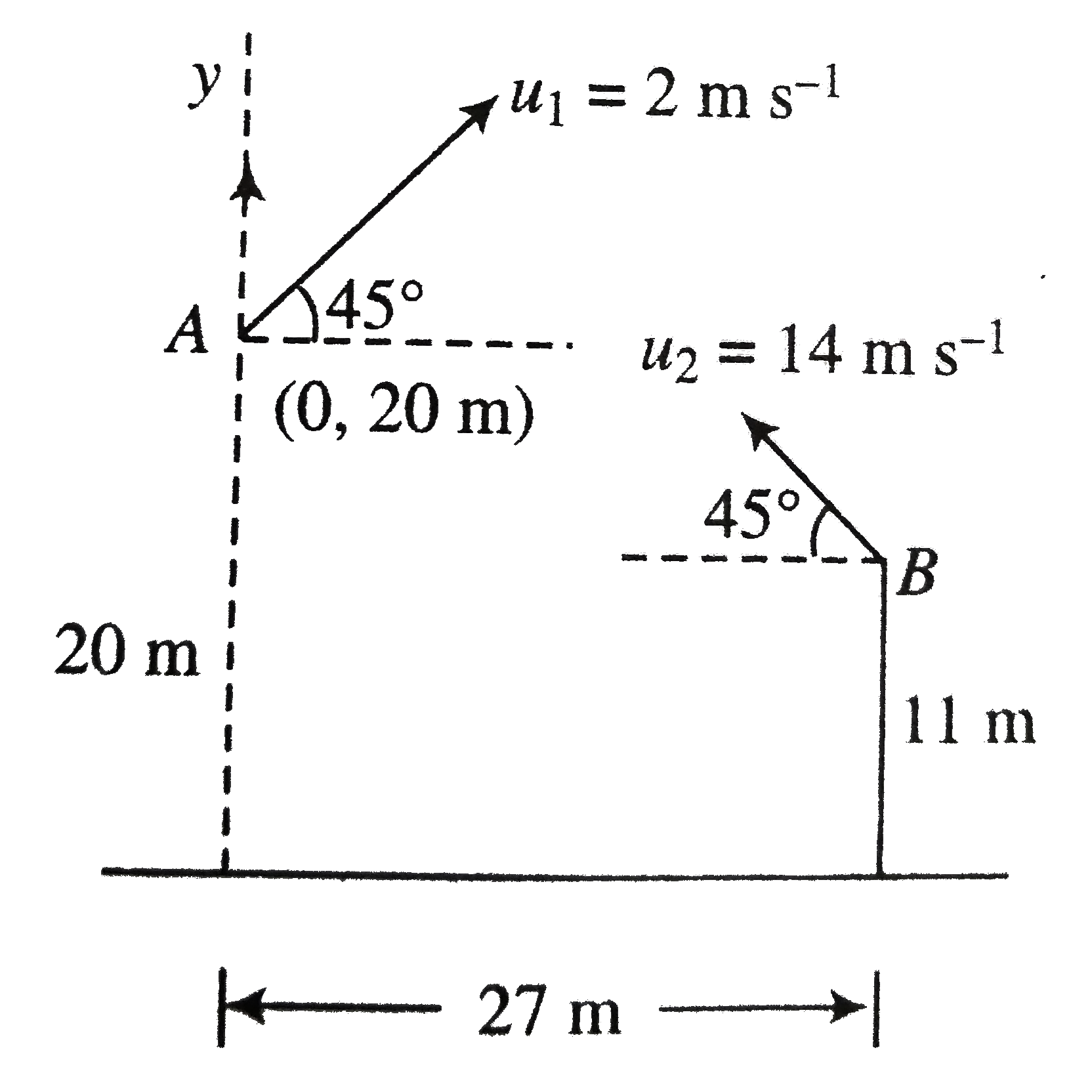
Minimum separation between A and B isA3 mB6 mC12 mD9 m
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
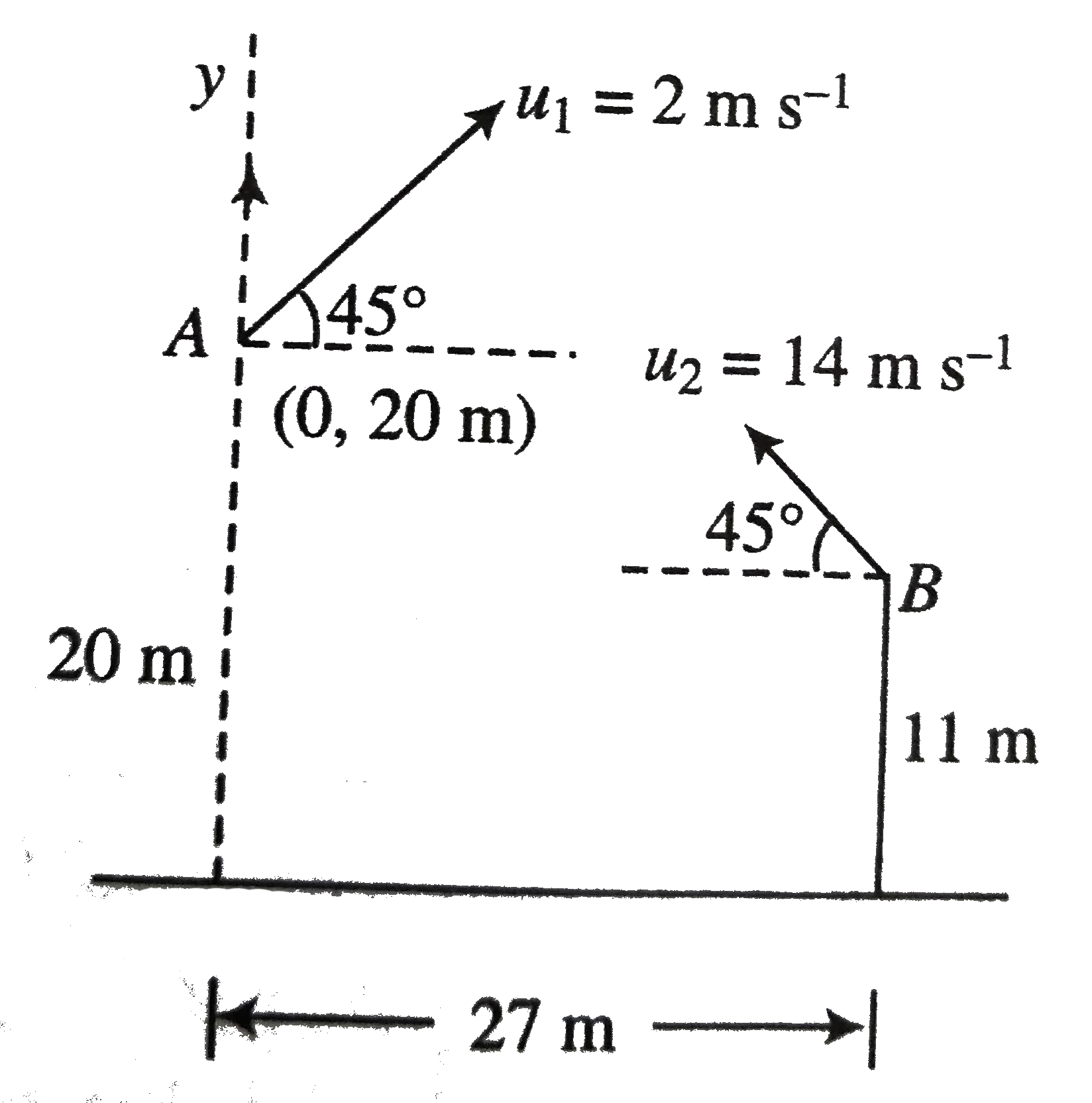
The relative velocity of B as seen from A in
View SolutionTwo particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if α is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
View SolutionTwo projectile A and B located at (0,0) and (4.4) respectively start moving simu ltaneou lsy with velocities VA=−4ˆi and VB=4ˆj:
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil be
View Solution
