A motor boat of mass m moves along a lake with velocity v0. At t = 0, the engine of the boat is shut down. Resistance offered to the boat is equal to σv2. Then distance covered by the boat when its velocity becomes v0/2 is
3mv02σ
v0mln22σ
2mIn2σ
mIn2σ
The correct Answer is:D
To solve the problem, we need to analyze the motion of the motorboat after the engine is shut down. The resistance acting on the boat is proportional to the square of its velocity. Let's break down the solution step by step.
Step 1: Understand the Forces Acting on the Boat
When the engine is shut down, the only force acting on the boat is the resistance force, which is given by:
R=σv2
where R is the resistance, σ is a constant, and v is the velocity of the boat.
Step 2: Apply Newton's Second Law
According to Newton's second law, the net force acting on the boat is equal to the mass of the boat multiplied by its acceleration:
ma=−R
Since the resistance is acting in the opposite direction to the motion, we can write:
ma=−σv2
Step 3: Relate Acceleration to Velocity
Acceleration a can be expressed in terms of velocity v and position x using the chain rule:
a=dvdt=dvdx⋅dxdt=vdvdx
Substituting this into the equation gives:
mvdvdx=−σv2
Step 4: Simplify the Equation
We can simplify the equation by dividing both sides by v (assuming v≠0):
mdvdx=−σv
Step 5: Rearranging the Equation
Rearranging gives us:
dvv=−σmdx
Step 6: Integrate Both Sides
We need to integrate both sides. The left side will be integrated from the initial velocity v0 to the final velocity v02, and the right side will be integrated from 0 to s (the distance covered):
∫v02v0dvv=−σm∫s0dx
This results in:
ln(vv0)∣∣∣v02v0=−σms
Step 7: Evaluate the Integrals
Evaluating the left side:
ln⎛⎝v02v0⎞⎠=ln(12)=−ln(2)
Thus, we have:
−ln(2)=−σms
Step 8: Solve for Distance s
Rearranging gives:
s=mln(2)σ
Final Answer
The distance covered by the boat when its velocity becomes v02 is:
s=mln(2)σ
When the engine is shut down, the only force acting on the boat is the resistance force, which is given by:
R=σv2
where R is the resistance, σ is a constant, and v is the velocity of the boat.
According to Newton's second law, the net force acting on the boat is equal to the mass of the boat multiplied by its acceleration:
ma=−R
Since the resistance is acting in the opposite direction to the motion, we can write:
ma=−σv2
Acceleration a can be expressed in terms of velocity v and position x using the chain rule:
a=dvdt=dvdx⋅dxdt=vdvdx
Substituting this into the equation gives:
mvdvdx=−σv2
We can simplify the equation by dividing both sides by v (assuming v≠0):
mdvdx=−σv
Rearranging gives us:
dvv=−σmdx
We need to integrate both sides. The left side will be integrated from the initial velocity v0 to the final velocity v02, and the right side will be integrated from 0 to s (the distance covered):
∫v02v0dvv=−σm∫s0dx
This results in:
ln(vv0)∣∣∣v02v0=−σms
Evaluating the left side:
ln⎛⎝v02v0⎞⎠=ln(12)=−ln(2)
Thus, we have:
−ln(2)=−σms
Rearranging gives:
s=mln(2)σ
The distance covered by the boat when its velocity becomes v02 is:
s=mln(2)σ
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
Explore 20 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
Explore 15 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
STATEMENT-1: A body is projected from the ground with kinetic energy K at an angle of 60° with the horizontal. If air resistance is neglected, its K.E. When it is at the highest point of its trajectory will be K/4
because
STATEMENT-2: At the highest point of the trajectory, the direction of velocity and acceleration of the body are perpendicular to each other
View SolutionWhich statements can be possible cases in one/two dimensional motion:
View SolutionThe velocity of a particle moving in the positive direction of x-axis varies as v=α√x where α is positive constant. Assuming that at the moment t=0, the particle was located at x=0, find (i) the time dependance of the velocity and the acceleration of the particle and (ii) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path.
View SolutionEnds of two wires A and B, having resistivityρA=3×105Ωm and ρB=6×10−5ωm of same cross section ara are pointed together to form a single wire. If the resistance of the joined wire does not change with temperature, then find the ratio of their lengths given that temperatue coefficient of resistitivy of wires A and B are α=4×10−5/∘C and α=−4×106/∘C . Assume that mechanical dimensions do not change with temperature.
View SolutionGenerally, we consider that during slowing of a moving automobile, its retardation is constant, but in practice this is seldom the case. Under many circumstances, especially at high speed, we usually apply the brakes slowly at first and then more strongly as the car slows. The braking force therefore depends on the time during the interval over which the car is slowing and acceleration changes with time.
ax(t)=vA−vxdt=Fx(t)m
∫vxv0xdVx=∫10Fx(t)mdt
∴Vx=V0x+1m∫10Fx(t)dt
x(t)=x0+∫10Vx(t)dt
An example for the same is discussed here.
A car of mass m = 1000 kg is moving with 25 m/s. The driver begins to apply the brakes so that the magnitude of the braking force increases linearly with time at a rate of 2000 N/s.
Read the above passage carefully and answer the following questions.
Find the velocity of the car at t = 10 sec.
View SolutionThe force of resistance encountered by water on a motor boat of mass m going in still water with velocity v is proportional to the velocity v. At t=0 when its velocity is v0, then engine shuts off. Find an expression for the position of motor boat at time t and also the distance travelled by the boat before it comes to rest. Take the proportionality constant as k>0.
View SolutionA boat of mass 40kg is at rest. A dog of mass 4kg moves in the boat with a velocity of 10m/s. What is the velocity of boat (nearly)?
View SolutionA boat of mass 50kg is at rest. A dog of mass 5kg moves in the boat with a velocity of 20m//s . What is the velocity of boat?
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. How long the motor boat with the shut down engine.
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. The velocity (v) of the motor boat as a function of the distance (s) covered with the shutdown engine is
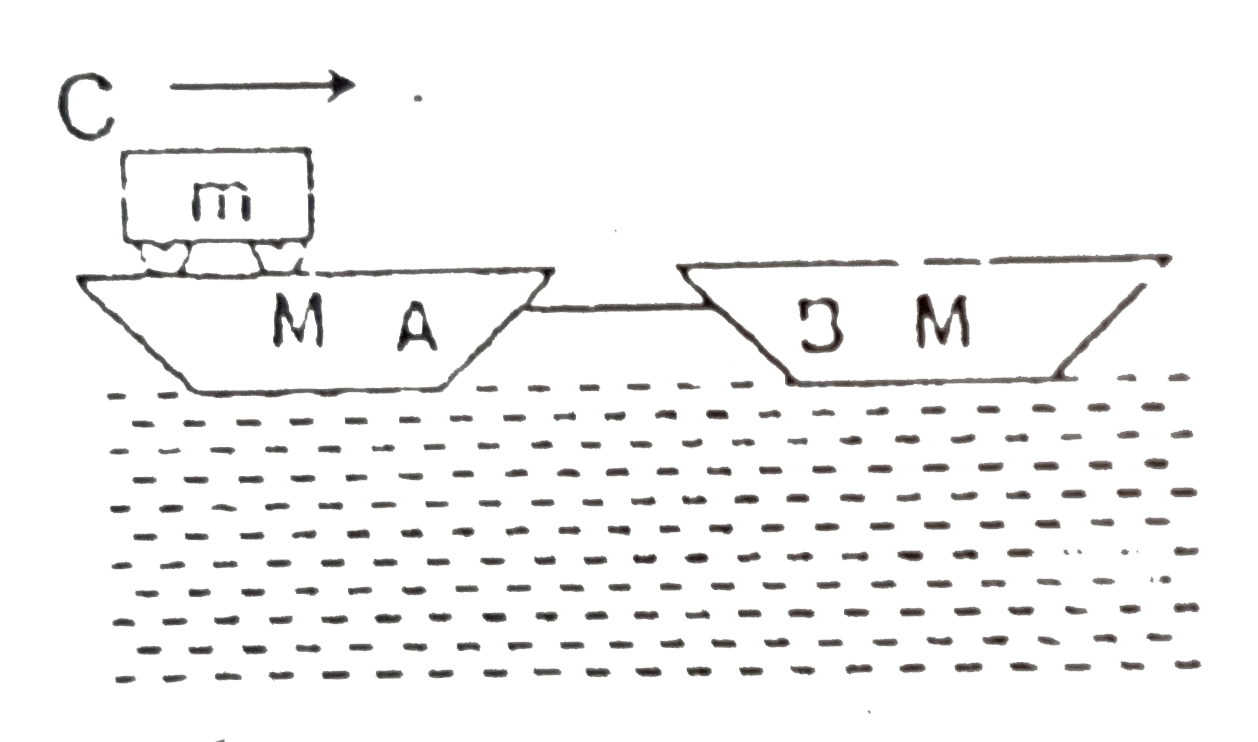
View SolutionA car C of mass m is initially at rest on the boat A of mass M tied to the identical boat B of some, mass M through a massless inextensible string as shown in the figure. The car accelerates from rest to velocity v0 with respect to boat A in time t0sec. At time t=t0 the car applies brake and comes to rest relative to boat in negligible time. Neglect friction between boat and water find the velocity of boat A just after applying brake.
View SolutionA motor-boat of mass m moves along a lake with velocity v0. At the moment t = 0 the engine of the boat is shut down. Assuming the resistance of the particle to-be proportional to the velocity of the boat F = - rv, find:
(a) How long the motor boat moved with the shut down engine,
(b) (b) The velocity of the motor boat as a function of the distance covered with the shutdown engine, as well as total distance covered till the complete stop.
(c ) The mean velocity of the motor boat over the time interval (beginning with the moment t=0), during which its velocity decreases η times.
View SolutionA motor boat of mass m moves along a lake with velocity V_(0) . At t = 0 , the engine of the boat is shut down. Magnitude of resistance force offered to the boat is equal to rV. (V is instantaneous speed). What is the total distance covered till it stops completely? [Hint: F(x) = mV(dV)/(dx) =- rV]
View SolutionA man of mass m jumps onto a boat which has a mass M. If the person has a horizontal component of velocity v relative to boat, just before he enters the boat and the boat is travelling at speed v0 away from the pier when he makes the jump, the resulting speed of man and boat is
View SolutionThe resistance offered by the stream of water on motor boat moving with uniform velocity of 30msec−1 is 5000 N. The power of motor boat is:
View SolutionThe force of resistance encountered by water on a motor boat of mass m going in still water with velocity v is proportional to the velocity v. At t=0 when its velocity is v0, then engine shuts off. Find an expression for the position of motor boat at time t and also the distance travelled by the boat before it comes to rest. Take the proportionality constant as k>0.
View Solution