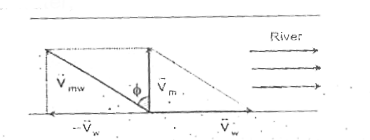
The speed of a man in a ponds is double that of the water ina river. The man starts swimming from a polints P on the bank. What is the angle of swimming of the man so as to directly to the opposite bank?
Let the man swim with certain speed in the ponds . That is the speed of the man w.r.t water (Vmw)
When the man swims in a river (moving water ) the velocity of the man is perpendicular to the river i.e
⇒¯¯¯Vm⊥¯¯¯Vw, if the swims at an angle ϕ w.r.t water ,
sin(ϕ)=VwVmw
⇒ϕ=sin−1(Vw)Vmw
Since the speed of water is halfy of that of the man realtive tom water (speed of the man in still water)
Vmw=2Vw
⇒VwVmw=12
Using (1) & (2) we getϕ=sin−1(12)=30∘
Thus the angle of swimming θ=90∘+ϕ=90∘+30∘=120∘ to the direction of flow of water
Related Playlists
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)10videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)14videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
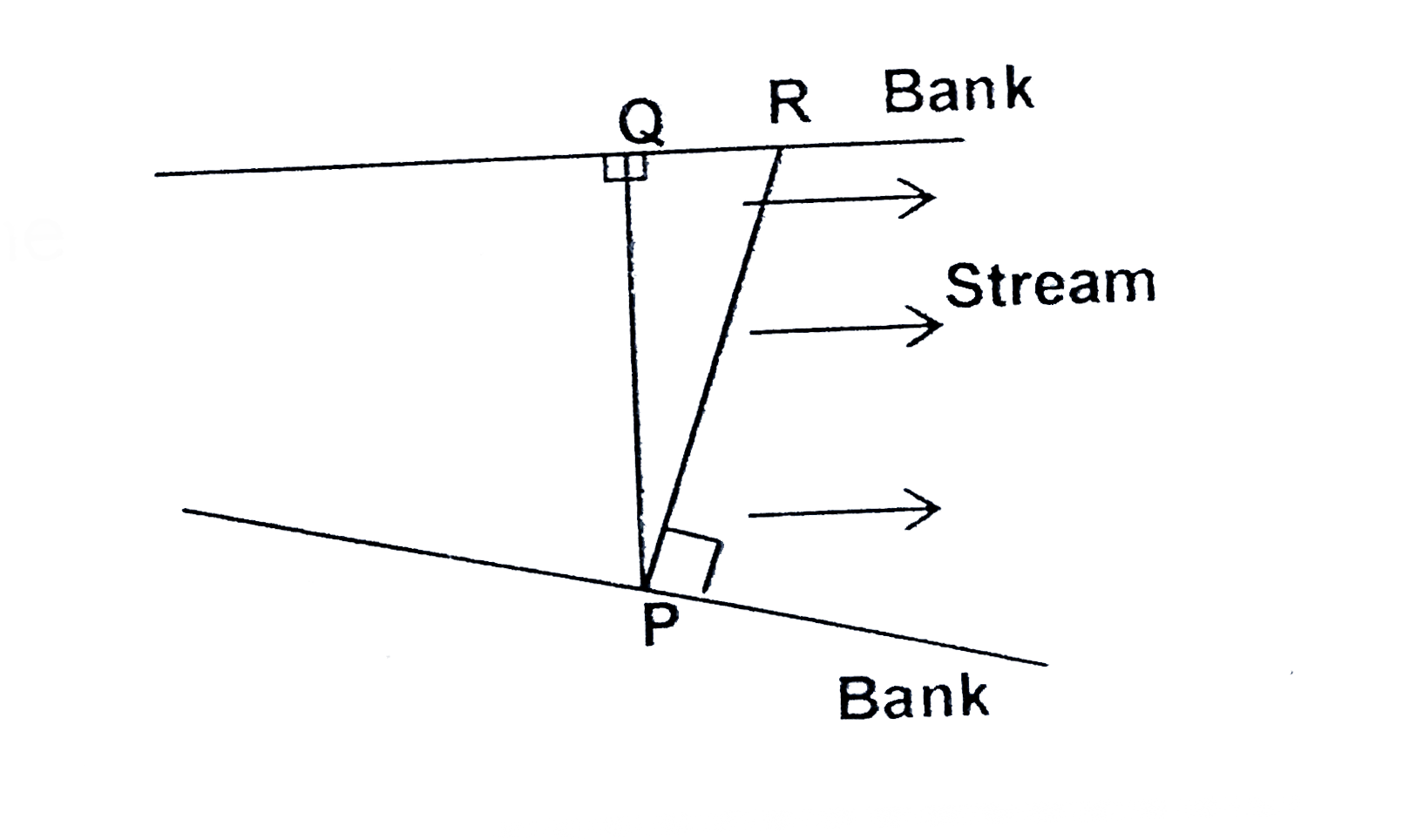
In a lake, stream direction is as shown in the figure. A man starting from the point P on the bank wants to move to the
 View Solution
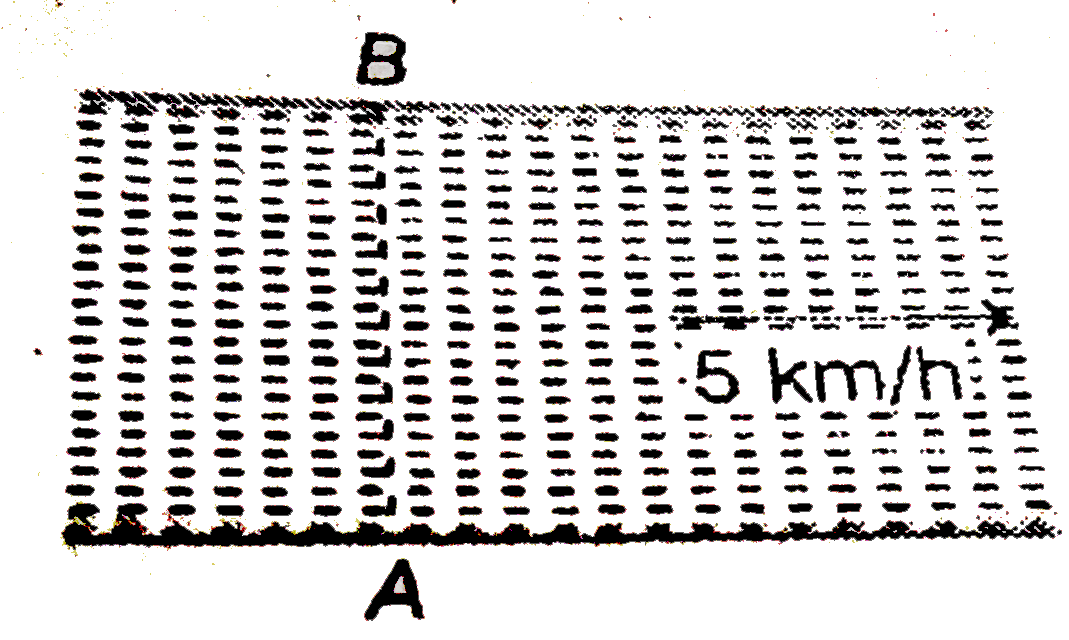
View SolutionInthe figure shown a river of width 4km is flowing with the speed of 5km/h. A swimmer whose swimming speed relative to the water is 4km/h, starts swimming from a points on a bank. On the other bank 5 is a point which is directly opposite to A. What minimum distance (in km) the swimmer will have to walk on the other bank to reach the point B.
 View Solution
View SolutionIn the figure shown a river of width 4km is flowing with speed of 5kim/h. A swimmer whose swimming speed relative to the wter is 4km/h, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (inkm) the swimmer will have to walk on the other bank to reach the point B.
 View Solution
View SolutionIn the previous problem, How far from the point directly opposite to the starting point does the man reach the opposite bank
View SolutionIf speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
View SolutionA man can swim in still water with a speed of 3m/s x and y axis are drawn along and normal to the bank of river flowing to right with a speed of 1m/s. The man starts swimming from origin O at t = 0 second. Assume size of man to be negligible. Find the equation of locus of all the possible points where man can reach at t = 1 sec
 View Solution
View SolutionAt what angle to the stream should a swimmer swim to reach the opposite bank as soon as possible?
View SolutionA swimmer can swim in still water with speed v and the river is flowing with speed v/2. What is the ratio of the time taken to swimming across the river in shortest time to that of swimming across the river over the shortest distance ?
View SolutionIn a river of 20 m width. Half part of river flows with speed 10m/sec and remaining half part flows with 20m/sec as shown in figure. A man starts to swim from A and reaches to point B in 10 sec. Man swims with speed Vm with respect to river at an angle θ with line AB. Then, angle θ will be : (man swims with constant speed and in same direction with respect to river throughout the motion):
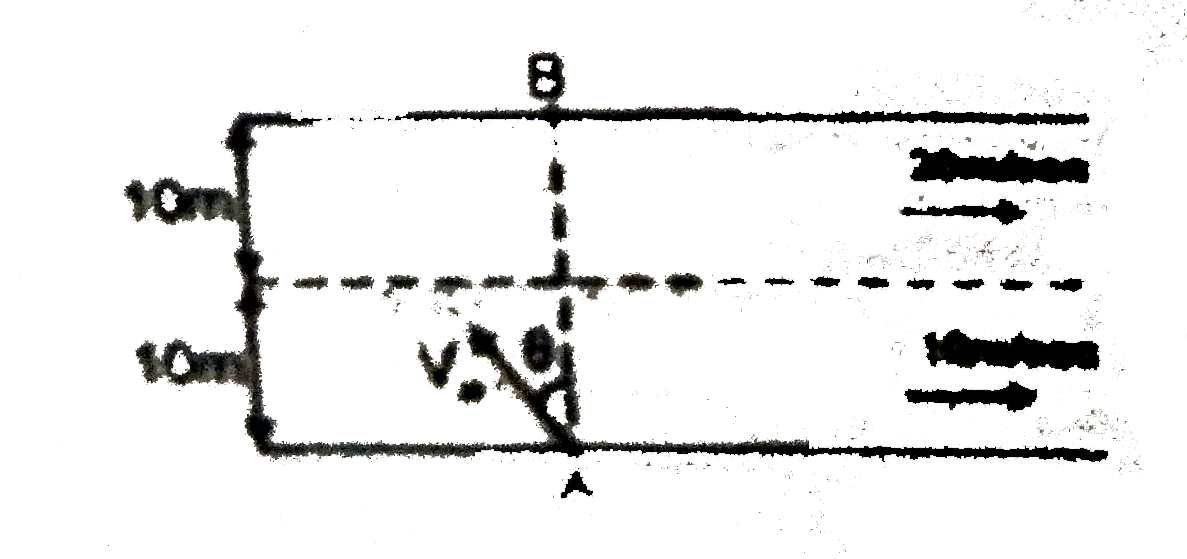 View Solution
View SolutionA man swims with a constant absolute velocity irrespective of the current in water. He can swim from a point P on one bank of river to a point Q just opposite the other in time t when the water is still. He takes time t1 to swim across along the same straight path PQ when the river flows down with a uniform velocity . The river velocity is btt1√(t21−t2)
where b is the breadth PQ of the river.View Solution


