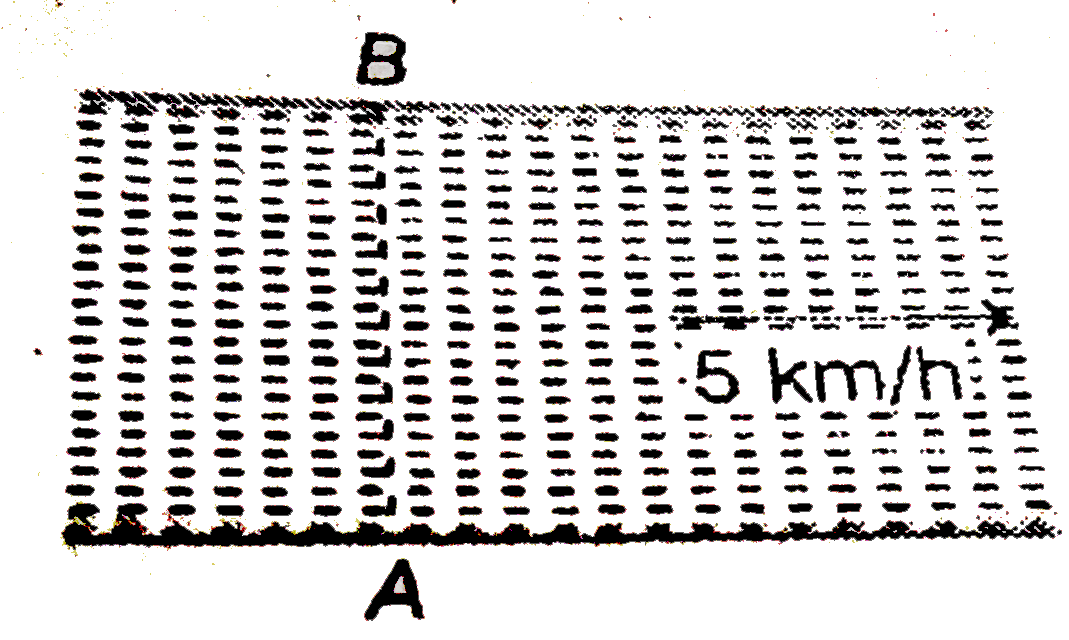
In the figure shown a river of width 4km is flowing with speed of 5kim/h. A swimmer whose swimming speed relative to the wter is 4km/h, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (inkm) the swimmer will have to walk on the other bank to reach the point B.
2
3
4
5
The correct Answer is:B
Step by step video, text & image solution for In the figure shown a river of width 4km is flowing with speed of 5kim//h. A swimmer whose swimming speed relative to the wter is 4km//h, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (inkm) the swimmer will have to walk on the other bank to reach the point B. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE27videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE19videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
Knowledge Check
- Question 1 - Select One
Inthe figure shown a river of width 4km is flowing with the speed of 5km/h. A swimmer whose swimming speed relative to the water is 4km/h, starts swimming from a points on a bank. On the other bank 5 is a point which is directly opposite to A. What minimum distance (in km) the swimmer will have to walk on the other bank to reach the point B.
 A2B3C4D5
A2B3C4D5 - Question 1 - Select One or More
A man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
AMan can directly reach point B in time d/l.BMan can cross the river in minimum time d/vCMan can reach point B directly in time d√v2−u2DIf u>v then man cannot reach the point B directly . - Question 1 - Select One
The stream of a river is flowing with a speed of 2 km/h. A swimmer can swim at a speed of 4 km/h. What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
A90∘B60∘C120∘D150∘ - Question 1 - Select One
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
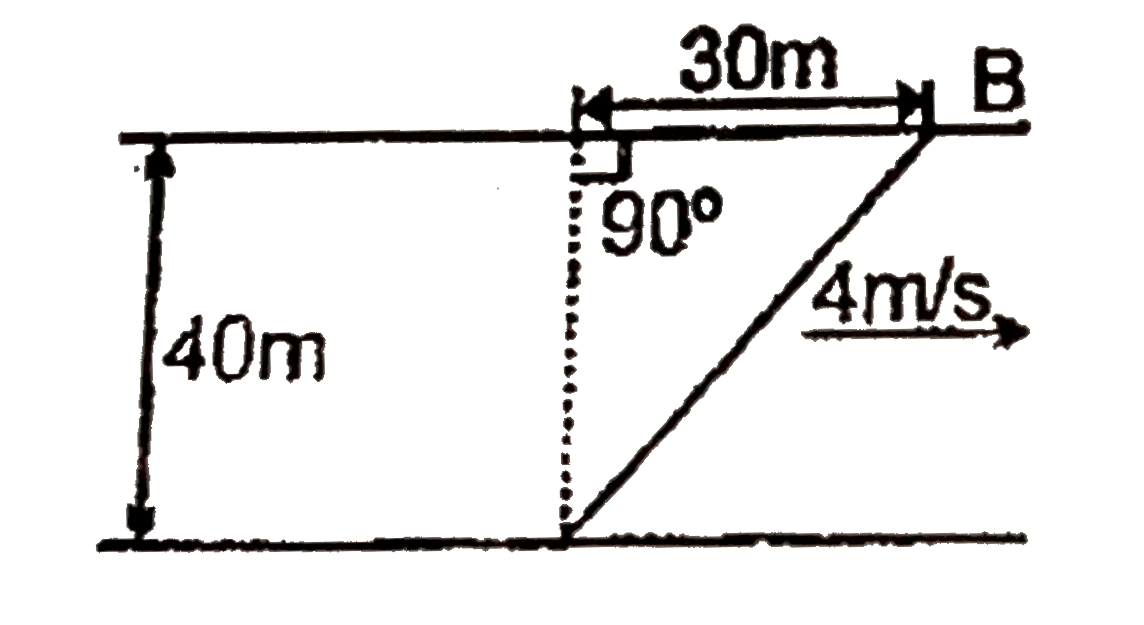 A8m/sB3.2m/sC6.5m/sD7√2m/s
A8m/sB3.2m/sC6.5m/sD7√2m/s
Similar Questions
The speed of a man in a ponds is double that of the water ina river. The man starts swimming from a polints P on the bank. What is the angle of swimming of the man so as to directly to the opposite bank?
View SolutionThe width of a rivers is 25m and in it water is flowing with a velocity of 4m/min . A boatman is standing on the bank of the river . He want to sail the boat to a point at the other bank which is directly opposite to him . In what time will he cross the river , if he can sail the boat at 8m/min. relative to the water ?
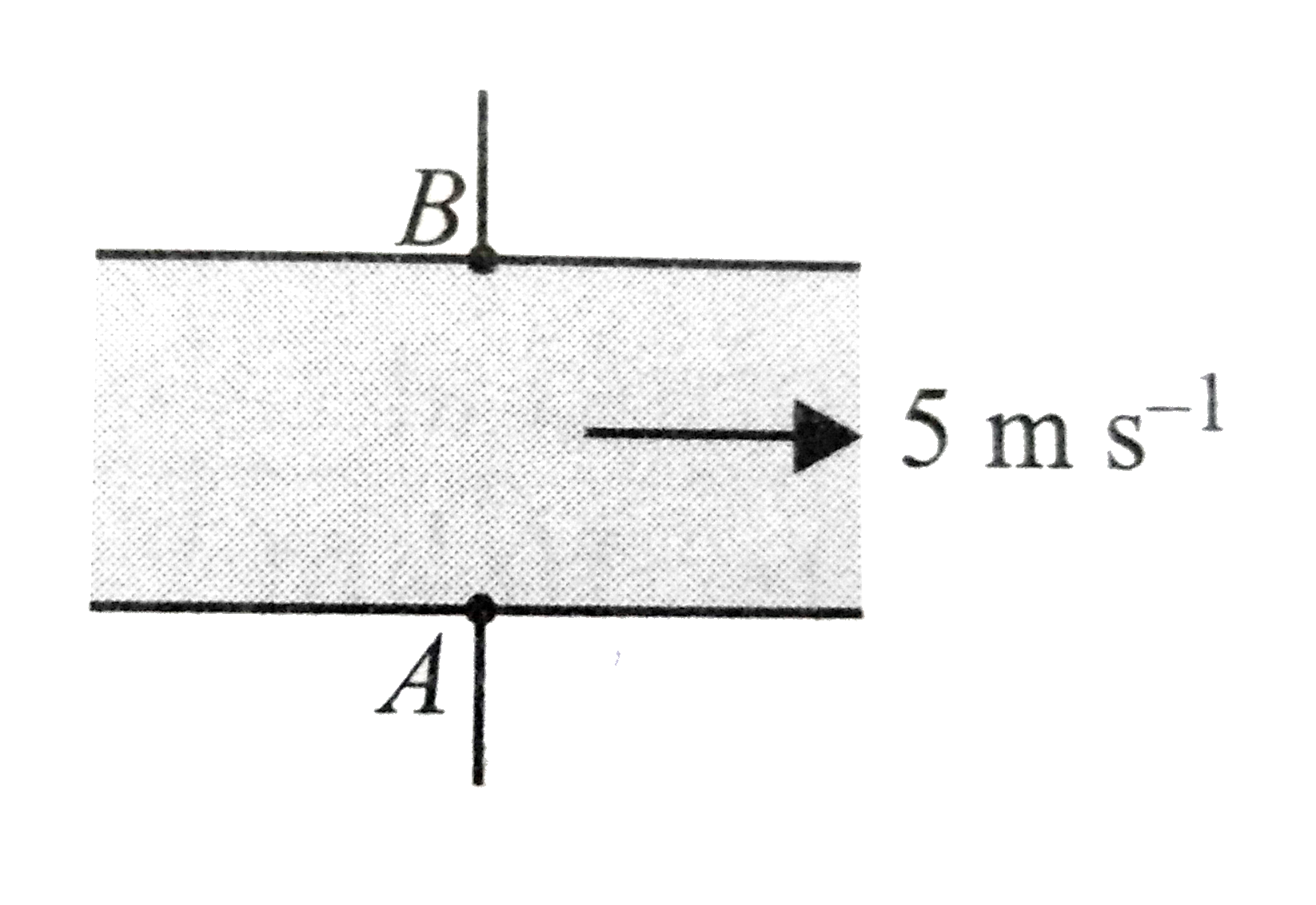
View SolutionA river is flowing from west to east with a speed 5 m s−1. A swimmer can swim in still water at a speed of 10 m s−1 .
If he wants to start from point A on south bank and reach opposite point B on north bank. In what direction direction should he swim ?
 View Solution
View SolutionA swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. The man has to reach the other shore at the point directly opposite to his starting point. If the reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
View SolutionA boat can swim in still water with speed of 20 km/h . a river of width 500 meters flows with speed of 6 km./h. In what direction . . . . should the boat be pointed , so that it reaches the opposite bank at the point directly opposite the starting point ? Also find the time . . . . . taken. Is this the least time of crossing ?
View SolutionA boat man can rown with a speed of 10kmh−1 in still water. If the river flows steadily at 5km/h, in which direction showld the boatman row in order to reach a point on the other bank directly opposite to the point from wher he stared ? The width of the river is 2km.
View Solution

