XYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90∘
Since, tangents drawn from an external point to a circle are equal.
∴ AP=AC
Thus, in △APO and △ACO,
∴ ⎧⎪⎨⎪⎩AP=ACAO=AO (common)OP=OC (radius of circle)
∴ By SSS cirterion of congruence, we have
△APO≅△ACO ⇒ ∠PAO=∠OAC (c.p.c.t.)
⇒ ∠PAC=2∠CAO
Similarly, we can prove that
∠CBO=∠OBQ ⇒ ∠CBQ=2∠CBO
Since, XY∣∣X'Y'
∠PAC+∠QBC=180∘
(sum of interior angles on the same side of transversal is 180∘)
∴ 2∠CAO+2∠CBO=180∘ ...(1)
⇒ ∠CAO+∠CBO=90∘
In △AOB,
⇒ ∠CAO+∠CBO+∠AOB=180∘ (angle sum property)
⇒ ∠CAO+∠CBO=180∘−∠AOB ...(2)
∴ From Eqs. (1) and (2), we get
180∘−∠AOB=90∘ ⇒ ∠AOB=90∘.
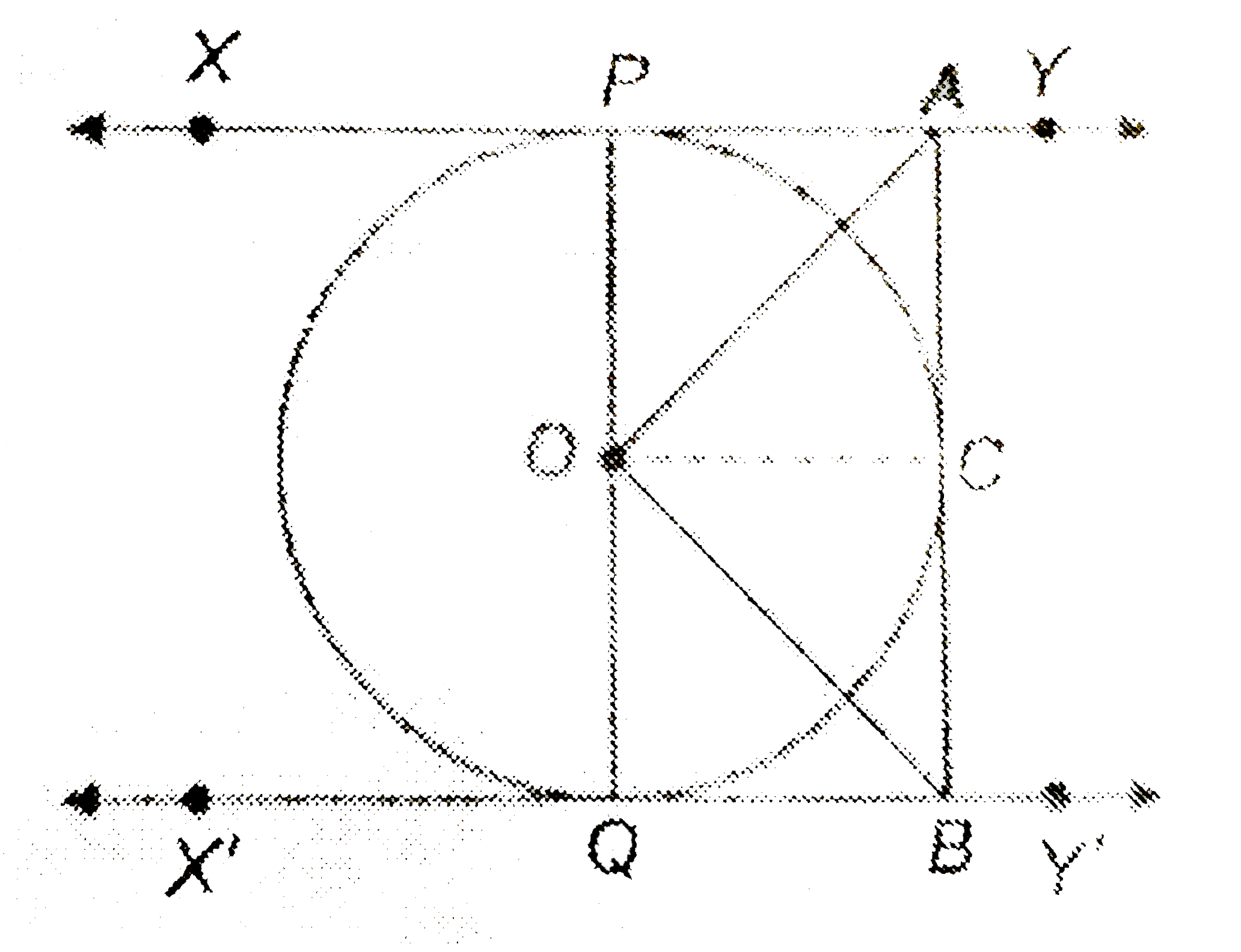 Hence Proved.
Hence Proved.
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise
25 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions
3 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
Similar Questions
In Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
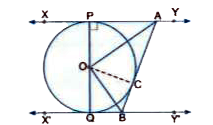
View SolutionXYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View Solution
Knowledge Check
PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
A60∘B120∘C90∘D180∘AB and AC are tangents to the circle with centre O. Then x equals.
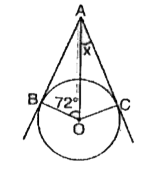 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘AB and AC are tangents to a circle with centre O. A is the external point of the circle. The line AO intersect the chord BC at D. The measure of the ∠BDOis
A60∘B90∘C45∘D75∘
landm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
View SolutionA tangent to y2=5x is parallel to the line y=4x+1 .Then the point of contact is
View SolutionIf x+2y=5 is tangent to the circle x2+y2=5, then equation of normal at their point of contact is
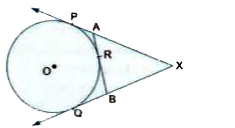
View SolutionIn Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
View Solution
