In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ=30∘. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
Since, PQ and PR are the tangents to a circle from an external point P.
∴ PQ=PR
⇒ ∠PRQ=∠PQR (angles opposite to equal sides are equal)
In △PQR
∠PQR+∠PRQ+∠QPR=180∘
⇒ ∠PQR+∠PQR+30∘=180∘
⇒ 2∠PQR=150∘ ⇒ ∠75∘
Again SR∣∣QP
∴ SRQ=RQP=75∘
Thus, PQR=QSR=75∘ (by alternate segment theorem)
In △QRS,
∠QRS+∠RSQ+∠SQR=180∘
∠SQR=180∘−75∘−75∘
⇒ ∠RQS=30∘
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise
25 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions
3 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
Similar Questions
In Figure, if tangents PAandPB are drawn to a circle such that ∠APB=300 and chord AC is drawn parallel to the tangent PB, then ∠ABC= 600 (b) 900 (c) 300 (d) None of these
View SolutionTangents AB and AC are drawn to a circle from a point A, such that ∠BAC=40∘. A chord CP is drawn parallel to BA. The measure of ∠CBP is:
View Solution
Knowledge Check
In figure , tangents PA and PB are drawn to a circle such that ∠APB=30∘ and chord AC is drawn parallel to the tangent PB then ∠ABC=
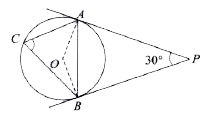 A60∘B50∘C30∘Dnone of these
A60∘B50∘C30∘Dnone of theseIn the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
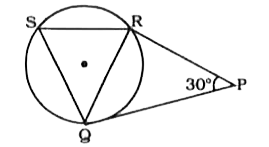 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘In the figure , PQ and PR are the tangents drawn form P to a circle with centre O. if ∠OPQ=35∘ then
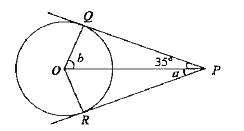 Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
In the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn Figure, common tangents PQandRs to two circle intersect at A. Prove that PQ=RS.
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O. IF ∠QPR=46∘ , then ∠QOR equals

View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if ∠QPR=90∘, then length of PQ is
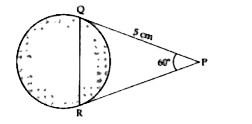
View SolutionIn the give figure ,PQ and PR are tangents to the given circle such that PQ =5 cm and ∠QPR=60∘. The length of chord QR is
View Solution
