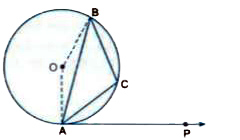
If AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
Given : Chord AB, diameter AOC and tangent at A of a circle with centre O.
To Prove : ∠BAT=∠ACB
Proof : Radius OA and tangent AT at A are perpendicular.
∴ ∠OAT=90∘ ⇒ ∠BAT=90∘−∠1 ...(2)
AOC is a diameter.
∴ ∠B=90∘ (angle in a semicircle is right angle)
⇒ ∠C+∠1=90∘ (angle sum property)
⇒ ∠C=90∘−∠1 ...(2)
From (1) and (2). we get ∠BAT=∠ACB
 Hence Proved.
Hence Proved.
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise
25 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions
3 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
Similar Questions
Knowledge Check
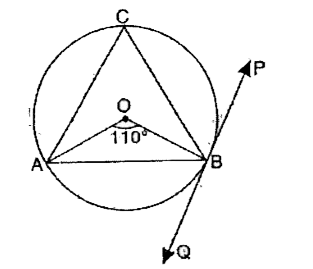
In the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
 A45∘B70∘C55∘D35∘
A45∘B70∘C55∘D35∘In a circle with centre O, AOC is a diameter of the circle, BD is a chord and OB and CD are joined. If ∠AOB =130∘, then ∠BDC is equal to
A30∘B25∘C50∘D60∘
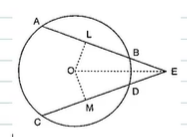
Two equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
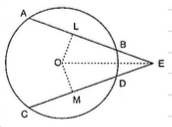
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure, Prove that BE=DE and AE=CE.
View SolutionIn a circel with centre O. chords AB and CD interest inside the circumference at E. Prove that ∠AOC+BOD=2∠AEC.
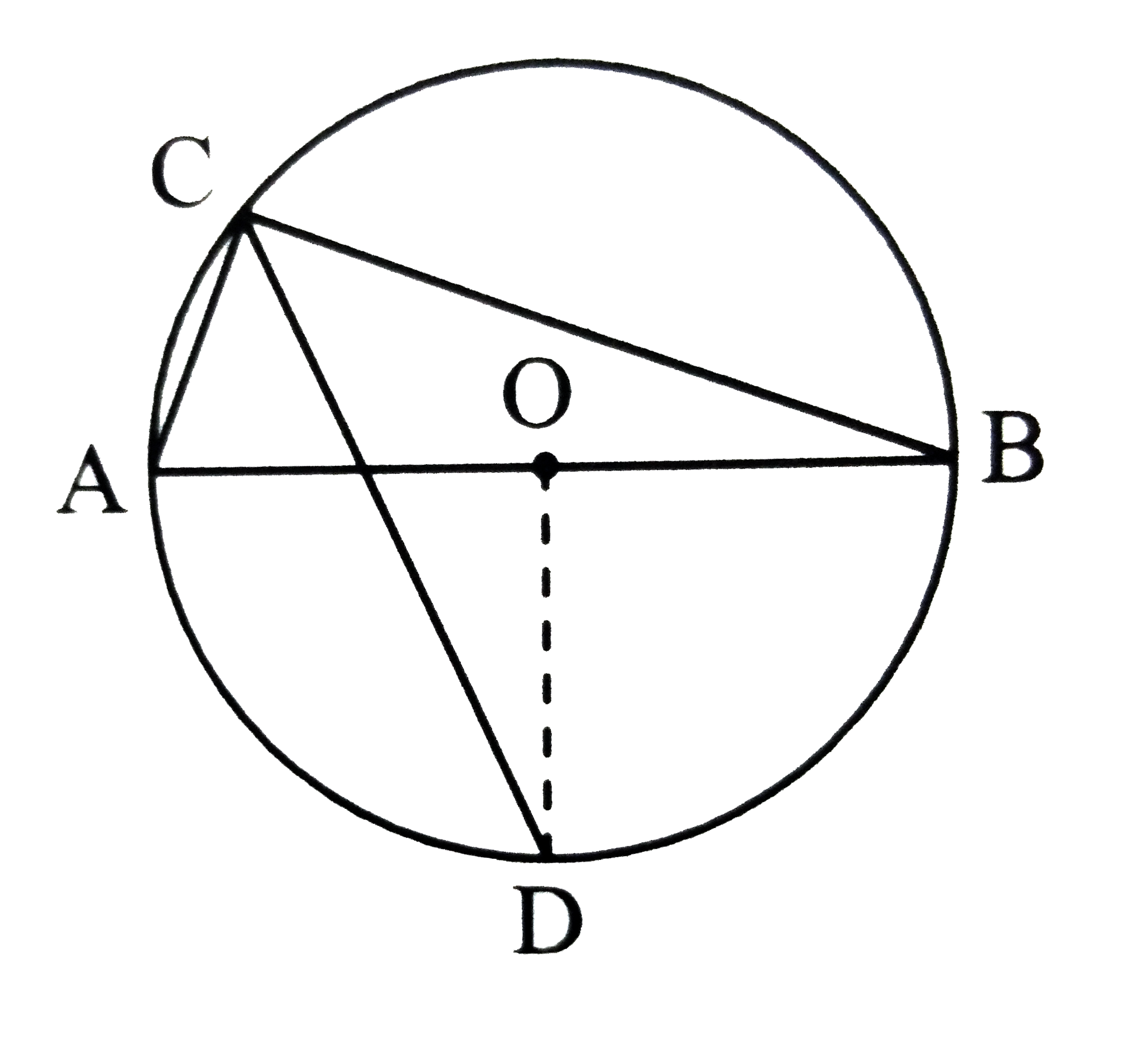
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
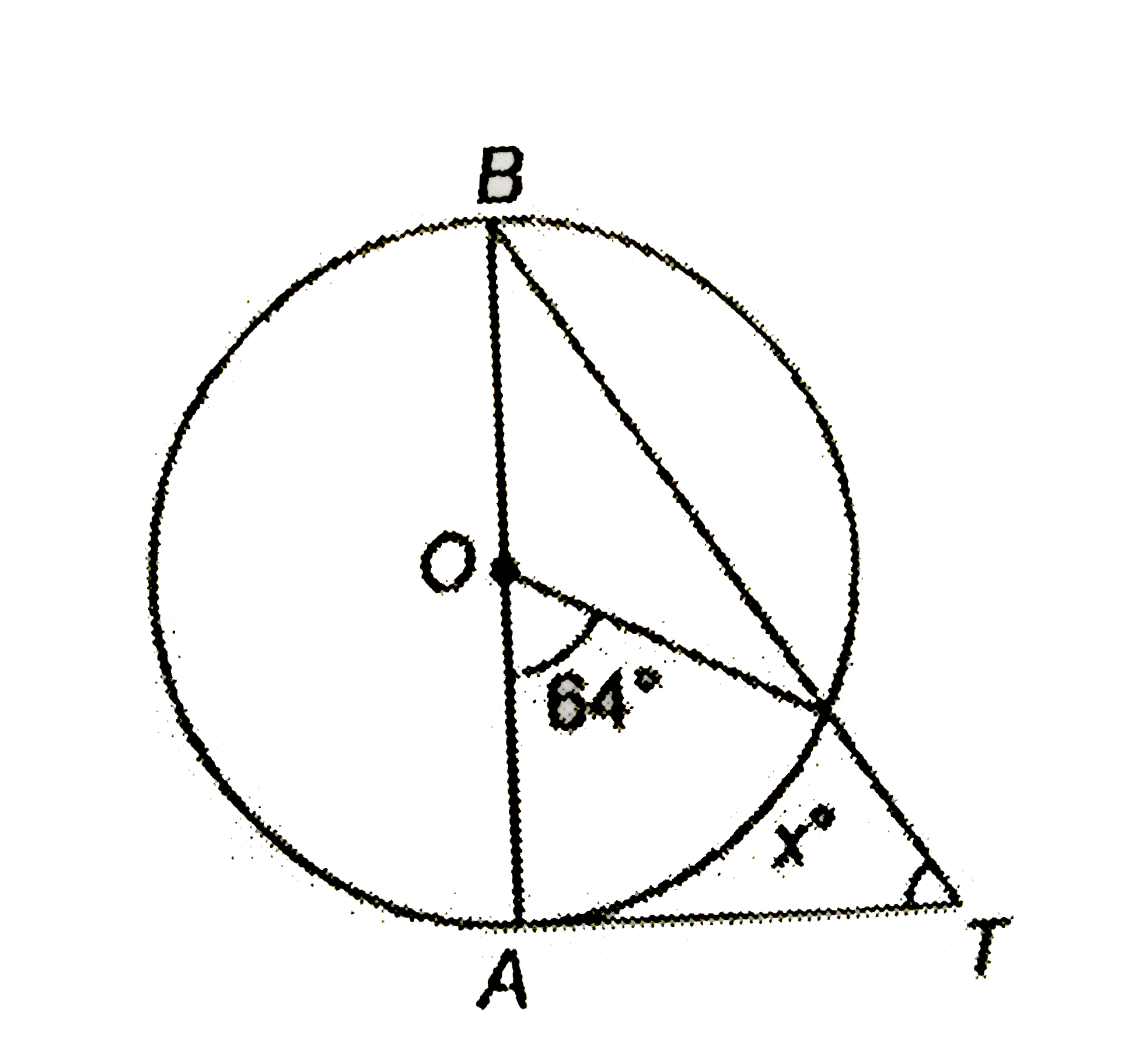
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
View Solution