A discrete random variable X has the probability distribution as given below

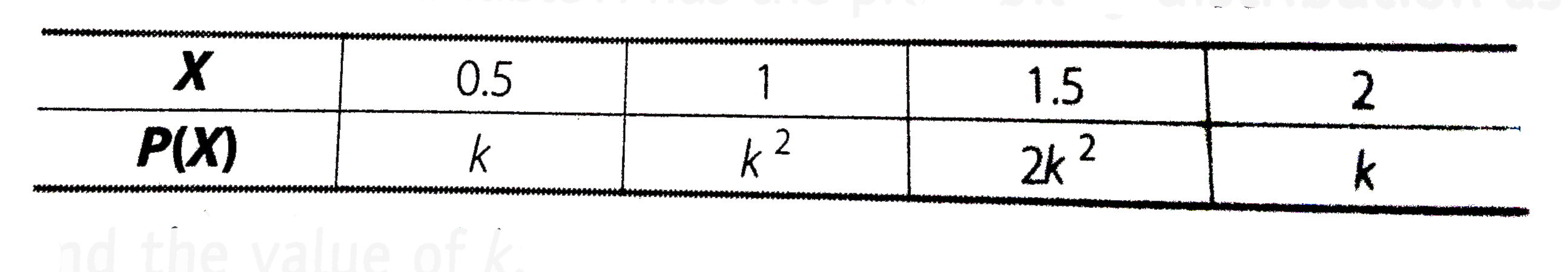
(i) Find the value of k.
(ii) Determine the mean of the distribution.

Video Solution

Text Solution

Verified by Experts

We have,

(i) We know that, $n \sum i = 1 P_{i} = 1,$ where $P_{i} \geq 0$
$\Rightarrow P_{1} + P_{2} + P_{3} + P_{4} = 1$
$\Rightarrow k + k^{2} + 2 k^{2} + k = 1$
$\Rightarrow 3 k^{2} + 2 k - 1 = 0$
$\Rightarrow 3 k^{2} + 3 k - k - 1 = 0$
$\Rightarrow (3 k - 1) (k + 1) = 0$
$\Rightarrow k = 1 / 3 \Rightarrow k = - 1$
Since, k is $\geq 0 \Rightarrow k = 1 / 3$
(ii) Mean of the distribution ( $μ$ )=E(X)= $n \sum i = 1_{i} x_{i} P_{i}$
$= 0.5 (k) + 1 (k^{2} + 1.5 (2 k^{2}) + 2 (k) = 4 k^{2} + 2.5 k$
$= 4 \cdot \frac{1}{9} + 2.5 \cdot \frac{1}{3}$
$= \frac{4 + 7.5}{9} = \frac{23}{18}$

Updated on:21/07/2023

|

Class 12 MATHS PROBABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

A random variable X has the probability distribution given below

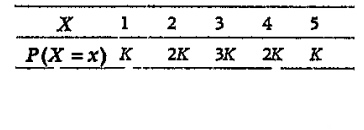
Its variance is
A $\frac{16}{3}$
B $\frac{4}{3}$
C $\frac{5}{3}$
D $\frac{10}{3}$
A random variable has the following probability distribution

The value of p is
A $\frac{1}{10}$
B-1
C $\frac{3}{10}$
DNone of these

NCERT EXEMPLAR-PROBABILITY-Probability

Home
Ask Doubt
Profile