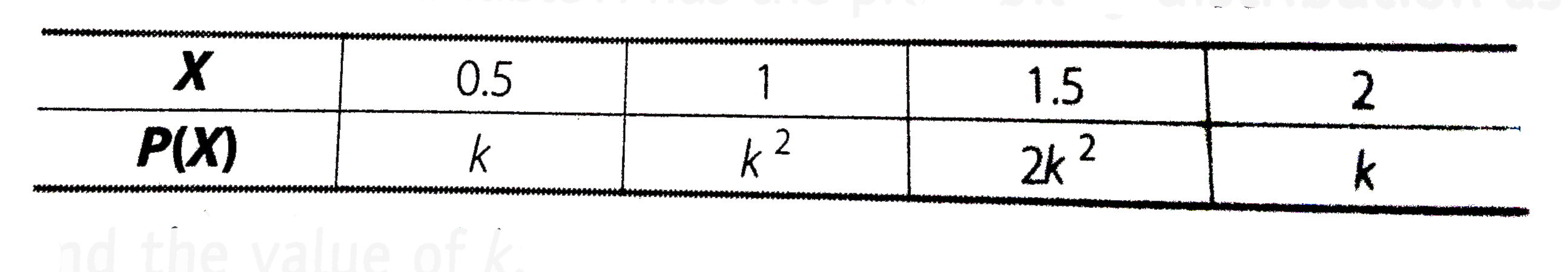A random variable X has the probability distribution given below
Its variance is

A
163
B
43
C
53
D
103
Video Solution
Text Solution
The correct Answer is:B
Given distribution is
∴ Variance =Σx2ip−(Σxip)2
=(1k+8k+27k+32k+25k)−(k+4k+9k+8k+5k)2
=(93k)−(27k)2=(93×19)−(27×19)2 [∴Σp=1,so k=19]
=939−9=93−819=129=43

|
Topper's Solved these Questions
- PROBABILITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - MHT CET Corner
4 Videos
- PROBABILITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - Exercise 1 (TOPICAL PROBLEMS)
44 Videos
- PRACTICE SET 24BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 24EXERCISE - Paper 2 (Mathmatics)
50 Videos
- SEQUENCES AND SERIES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 31
1 Video
Similar Questions
Knowledge Check
A random variable X has the following probability distribution

Then the variance of this distribution isA0.6B0.7C0.77D0.66A random variable X has the probability distribution

For the events E = { X is prime number} and F={x<4} then P(E∪F) isA0.50B0.77C0.35D0.87A random variable X has the probability distribution
For the events E = {X is a prime number} abd F={X<4},P(E∪F) is
 A0.87B0.77C0.35D0.50
A0.87B0.77C0.35D0.50
A random variable X has the following probability distribution find K.

View SolutionA discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k i. Find the value of k. ii. Determine the mean of the distribution.
View SolutionA random variable X has the probability distribution
For the events E = {X is a prime number} abd F={X<4},P(E∪F) is

View SolutionLet 'X' be a discrete random variable. The probability distribution of X is given below :
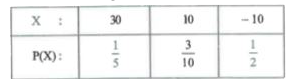
Then E(X) is equal to :
View SolutionLet 'X' be a discrete random variable. The probability distribution of X is given below :
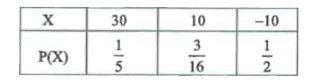
Then E(X) is equal to:
View Solution