A discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k i. Find the value of k. ii. Determine the mean of the distribution.
The correct Answer is:when k=13 the mean is 1.28
and when k=−1 the mean is 1.5
We know that in Probability distribution sum of all Probabilities is equal to 1
Σpi=1
⇒k+k2+2k2+k=1
⇒3k2+2k=1
⇒3k2+2k−1=0
⇒3k2+3k−k−1=0
⇒3k(k+1)−1(k+1)=0
⇒(3k−1)(k+1)=0
⇒3k−1=0⇒k=13
⇒k+1=0⇒k=−1
If the value of k=13 then the probability distribution be
P(X):13 19 29 13
Now the mean is:
E(X)=Σxi⋅pi
E(X)=0.5×13+1×19+1.5×29+2×13=16+19+13+23
118[3+2+6+12]=118[23]=1.28
If we take k=−1 then the probability distribution be:
P(X):−1 1 2 −1
Now the mean is:
E(X)=Σxi⋅pi
E(X)=0.5×(−1)+1×1+1.5×2+2×(−1)=−0.5+1+3−2=1.5
So when k=13 the mean is 1.28
and when k=−1 the mean is 1.5
Topper's Solved these Questions
Similar Questions
Knowledge Check
A discrete random variable X has the following probability distribution

The value of C and the mean of the distribution areA110 and 3.66B120 and 2.66C115 and 1.33DNone of these
A discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k i. Find the value of k. ii. Determine the mean of the distribution.
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA discrete random variable X has the probability distribution as given below
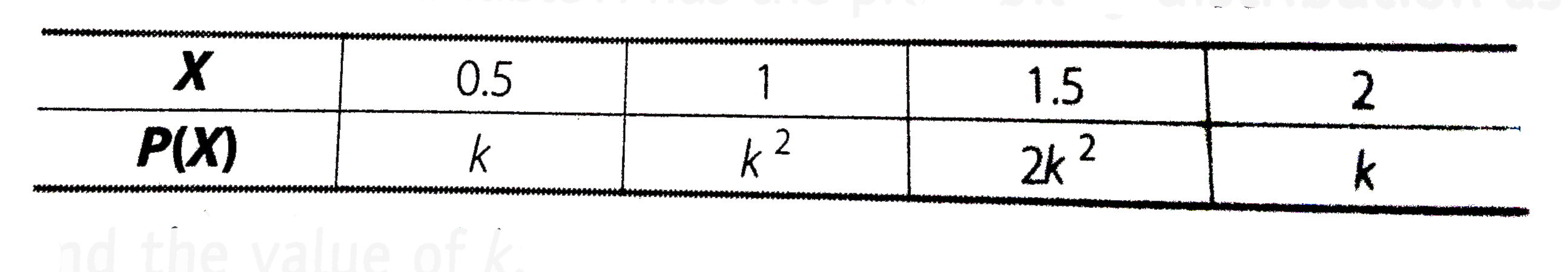
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA random variable X has the following probability distribution:
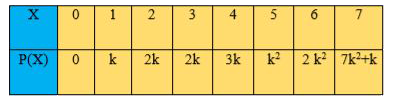
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionA random variable X has the following probability distribution: Values of X: −2 −1 0 1 2 3 P(X):0.1 k 0.2 2k 0.3 k
View SolutionThe probability distribution of X is as follows:
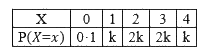
Find k and P [X<2].
View SolutionA discrete random variable X has the following probability distribution
the value of C and the mean of the distribution are
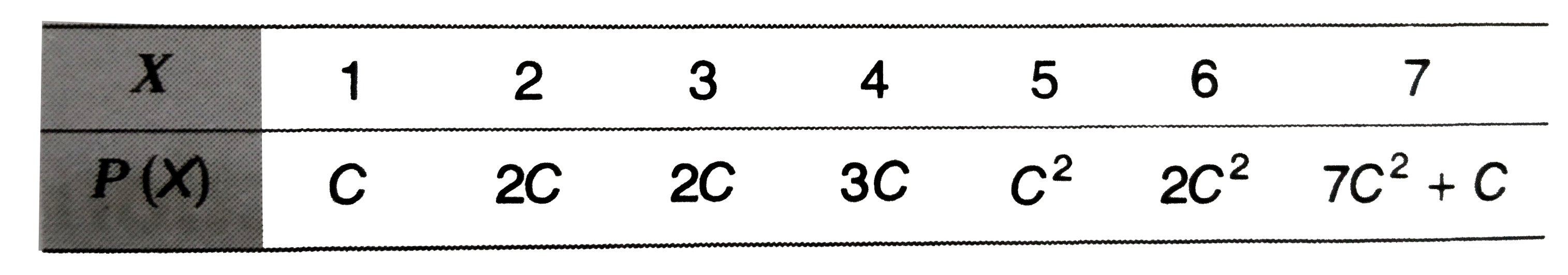
View Solution



