Pair of fair dice is thrown. Let X be the random variable which denotes the minimum of the two numbers which appear. Find the probability distribution, mean and variance of X.
The correct Answer is:Mean, E(X)=2.53 and Variance, var(X)=1.96
To solve the problem, we need to find the probability distribution, mean, and variance of the random variable X, which denotes the minimum of the two numbers that appear when a pair of fair dice is thrown.
Step 1: Determine the Sample Space
When two dice are thrown, the total number of outcomes is 6×6=36.
Step 2: Identify the Possible Values of X
The random variable X can take values from 1 to 6, as the minimum of two dice can be any of these numbers.
Step 3: Calculate the Probability Distribution of X
1. For X=1:
- The outcomes where the minimum is 1 are:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(3,1),(4,1),(5,1),(6,1).
- Total outcomes = 11.
- Probability P(X=1)=1136.
2. For X=2:
- The outcomes where the minimum is 2 are:
(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(4,2),(5,2),(6,2).
- Total outcomes = 9.
- Probability P(X=2)=936=14.
3. For X=3:
- The outcomes where the minimum is 3 are:
(3,3),(3,4),(3,5),(3,6),(4,3),(5,3),(6,3).
- Total outcomes = 7.
- Probability P(X=3)=736.
4. For X=4:
- The outcomes where the minimum is 4 are:
(4,4),(4,5),(4,6),(5,4),(6,4).
- Total outcomes = 5.
- Probability P(X=4)=536.
5. For X=5:
- The outcomes where the minimum is 5 are:
(5,5),(5,6),(6,5).
- Total outcomes = 3.
- Probability P(X=5)=336=112.
6. For X=6:
- The only outcome where the minimum is 6 is:
(6,6).
- Total outcomes = 1.
- Probability P(X=6)=136.
Step 4: Write the Probability Distribution
The probability distribution of X is as follows:
P(X=1)=1136P(X=2)=936=14P(X=3)=736P(X=4)=536P(X=5)=336=112P(X=6)=136
Step 5: Calculate the Mean of X
The mean (expected value) E(X) is calculated as follows:
E(X)=∑(xi⋅P(X=xi))
E(X)=1⋅1136+2⋅936+3⋅736+4⋅536+5⋅336+6⋅136
E(X)=11+18+21+20+15+636=9136≈2.53
Step 6: Calculate the Variance of X
The variance Var(X) is calculated using the formula:
Var(X)=E(X2)−(E(X))2
First, we calculate E(X2):
E(X2)=∑(x2i⋅P(X=xi))
E(X2)=12⋅1136+22⋅936+32⋅736+42⋅536+52⋅336+62⋅136
E(X2)=11+36+63+80+75+3636=30136≈8.36
Now, substituting back to find variance:
Var(X)=E(X2)−(E(X))2=30136−(9136)2
Var(X)=30136−82811296
Var(X)=301⋅36−82811296=10836−82811296=25551296≈1.96
Final Results
- Probability Distribution:
P(X=1)=1136,P(X=2)=936,P(X=3)=736,P(X=4)=536,P(X=5)=336,P(X=6)=136
- Mean: E(X)≈2.53
- Variance: Var(X)≈1.96
When two dice are thrown, the total number of outcomes is 6×6=36.
The random variable X can take values from 1 to 6, as the minimum of two dice can be any of these numbers.
- The outcomes where the minimum is 1 are:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(3,1),(4,1),(5,1),(6,1).
- Total outcomes = 11.
- Probability P(X=1)=1136.
- The outcomes where the minimum is 2 are:
(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(4,2),(5,2),(6,2).
- Total outcomes = 9.
- Probability P(X=2)=936=14.
- The outcomes where the minimum is 3 are:
(3,3),(3,4),(3,5),(3,6),(4,3),(5,3),(6,3).
- Total outcomes = 7.
- Probability P(X=3)=736.
- The outcomes where the minimum is 4 are:
(4,4),(4,5),(4,6),(5,4),(6,4).
- Total outcomes = 5.
- Probability P(X=4)=536.
- The outcomes where the minimum is 5 are:
(5,5),(5,6),(6,5).
- Total outcomes = 3.
- Probability P(X=5)=336=112.
- The only outcome where the minimum is 6 is:
(6,6).
- Total outcomes = 1.
- Probability P(X=6)=136.
The probability distribution of X is as follows:
The mean (expected value) E(X) is calculated as follows:
E(X)=1⋅1136+2⋅936+3⋅736+4⋅536+5⋅336+6⋅136
E(X)=11+18+21+20+15+636=9136≈2.53
The variance Var(X) is calculated using the formula:
E(X2)=12⋅1136+22⋅936+32⋅736+42⋅536+52⋅336+62⋅136
E(X2)=11+36+63+80+75+3636=30136≈8.36
Var(X)=30136−82811296
Var(X)=301⋅36−82811296=10836−82811296=25551296≈1.96
- Probability Distribution:
P(X=1)=1136,P(X=2)=936,P(X=3)=736,P(X=4)=536,P(X=5)=336,P(X=6)=136
Topper's Solved these Questions
Similar Questions
Pair of fair dice is thrown. Let X be the random variable which denotes the minimum of the two numbers which appear. Find the probability distribution, mean and variance of X.
View SolutionA fair die is tossed. Let X denote twice the number appearing. Find the probability distribution, mean and variance of X.
View Solution
Knowledge Check
A random variable X has the probability distribution given below
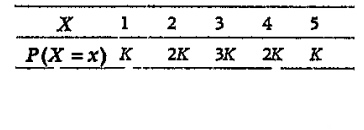
Its variance isA163B43C53D103
Consider the probability distribution of a random variable X.

Variance of X
View SolutionA fair coin is tossed four times. Let X denote the number of heads occurring. Find the probability distribution, mean and variance of X.
View SolutionA coin is tossed 4 times. Let X denote the number of heads. Find the probability distribution of X. Also, find the mean and variance of X.
View SolutionA fair die is tossed. Let X denote 1 or 3 according as an odd or an even number appears. Find the probability distribution, means variance of X.
View SolutionTwo numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of X. Find the mean and variance of this distribution.
View SolutionA random variable X has the probability distribution given below
Its variance is

View SolutionLet a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.
View Solution

