If the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
Video Solution
Text Solution
(i) Since the sum of probabilities in a probability distribution is always 1.
∴P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
⇒c+2c+4c+4c=1
⇒11c=1
⇒c=111
Then ,<br><br>P(X≤2)=P(X=1)+P(X=2)=110+210=311
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The probability distribution of a discrete random variable X is given below

The value of k isA8B16C32D48The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2The probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, isA1.76B2.45C3.2D4.8
If the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability of a random variable X is given below
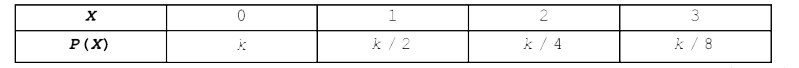
Find P(X≤2)+P(X>2)
View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is a. 8 b. 16 c. 32 d. 48
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View Solution


