If x is the number of tails in three tosses of a coin, then determine the standard deviation of X.

Video Solution

Text Solution

Verified by Experts

Given that, random variable X is the number of tails in three toses of the coin.
So, X=0,1,2,3.

$\Rightarrow P (X = x) =^{n} C_{x} {(p)}^{x} q^{n - x}$
Where n=3,p $= 1 / 2$ andx=0,1,2,3

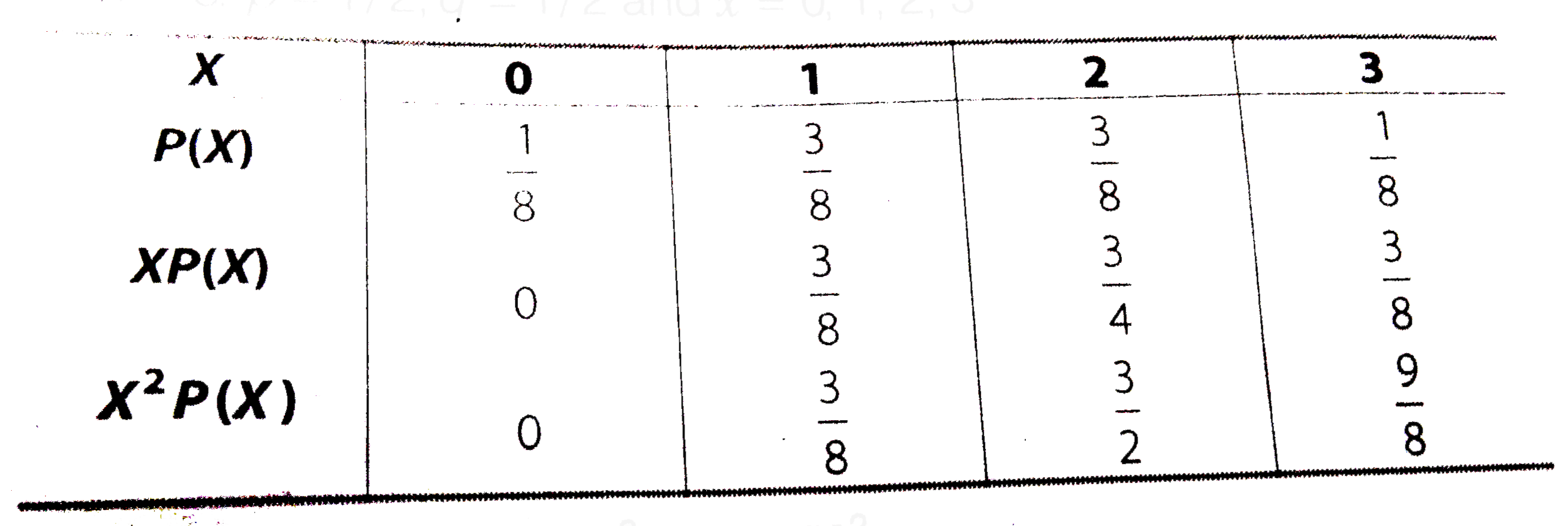
We know that, Var(X)= $E (X^{2}) - {[E (X)]}^{2}$
where, $E (X^{2}) = \sum_{i = 1}^{n} x_{i}^{2} P (x_{i}) and E (X) = \sum_{i = 1}^{n} x_{i} P (x_{i})$
$∴ E (X^{2}) = \sum_{i = 1}^{n} x_{i}^{2} P (X_{i}) = 0 + \frac{3}{8} + \frac{3}{2} + \frac{9}{8} = \frac{24}{8} = 3$
and ${[E (X)]}^{2} = {[\sum_{i = 0}^{n} x_{i}^{2} P (x_{i})]}^{2} = {[0 + \frac{3}{8} + \frac{3}{4} + \frac{3}{8}]}^{2} = {[\frac{12}{8}]}^{2} = \frac{9}{4}$
$∴ V a r (X) = 3 - \frac{9}{4} = \frac{3}{4}$
and standard deviation of X= $\sqrt{V a r (X)} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}$

Updated on:21/07/2023

Find the mean number of heads in three tosses of a fair coin.
A $\frac{3}{2}$
B $\frac{5}{2}$
C $\frac{1}{2}$
D $\frac{1}{8}$
The mean of getting tail two tosses of a coin is:
A $1 / 4$
B $1 / 3$
C $1 / 2$
D $1$
A coin is tossed 10 times. The number of heads minus the number of tails in 10 tosses is considered as the outcome of the experiment. What is the number of points in the sample space ?
A10
B11
C21
D99