A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
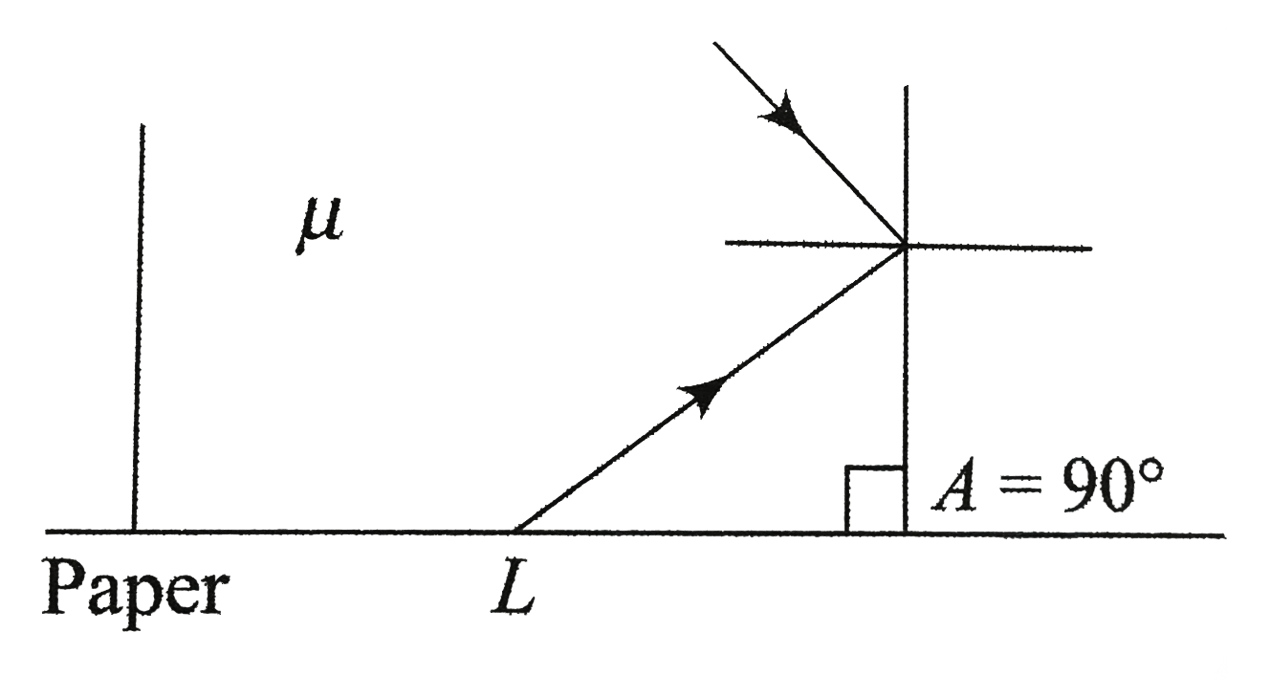
The situation is depicted in figure. Light will not emerge out from the vertical face BC if at it I>θCorsinI>sinθC⇒sinI>1μ[assinθC=1μ]…(i)
But from Snell's law at O1×sinθ=μsinr
And in ΔOPR,r+90+i=180⇒r+i=90∘⇒r=90−i
_S01_011_S01.png)
So sinθ=μsin(90−i)=μcosi⇒cosi=sinθμ
so sini=√1−cos2i=√1−[sinθμ]2....(ii)
so substituting the value of sin i from equation (ii) in (i),
√1−sin2θμ2>1μ i.e., μ2>1+sin2θ
∵(sin2θ)max=1∴μ2>2√2∴μmin=√2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES84videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
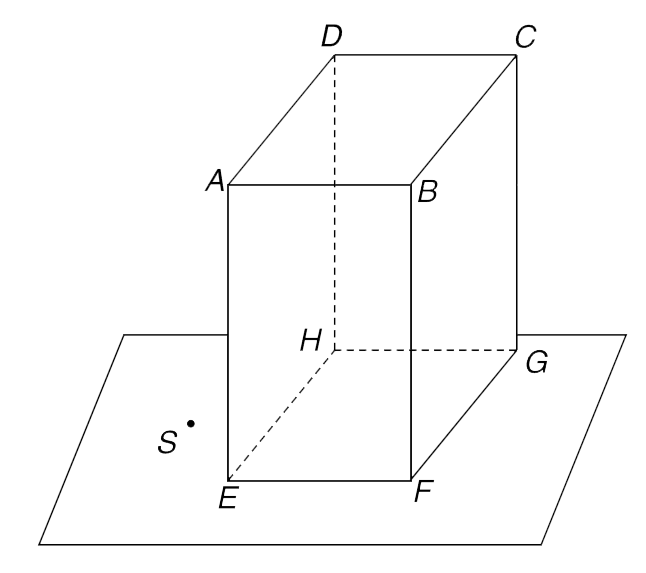
A large rectangular glass block of refractive index μ is lying on a horizontal surface as shown in Figure. Find the minimum value of μ so that the spot S on the surface cannot be seen through top plane ‘ABCD’ of the block.
 View Solution
View SolutionIn the figure shown, μ1>μ2. Find minimum value of i so that TIR never takes place at P.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
A√2B√3C√5D√5/√3 - Question 2 - Select One
Word ‘Newton’s printed on a paper and is placed on a horizontal surface below a cubical glass. The minimum value of refractive index of a cubical glass for which letters are not visible from any vertical faces, of the glass, is (Critical angle =45°)
A√3B0.5C1D√2 - Question 3 - Select One
In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
A block is rotating in contact with vertical wall (rotor) as shown. Find the minimum value of ω so that the block does not slide down.
 View Solution
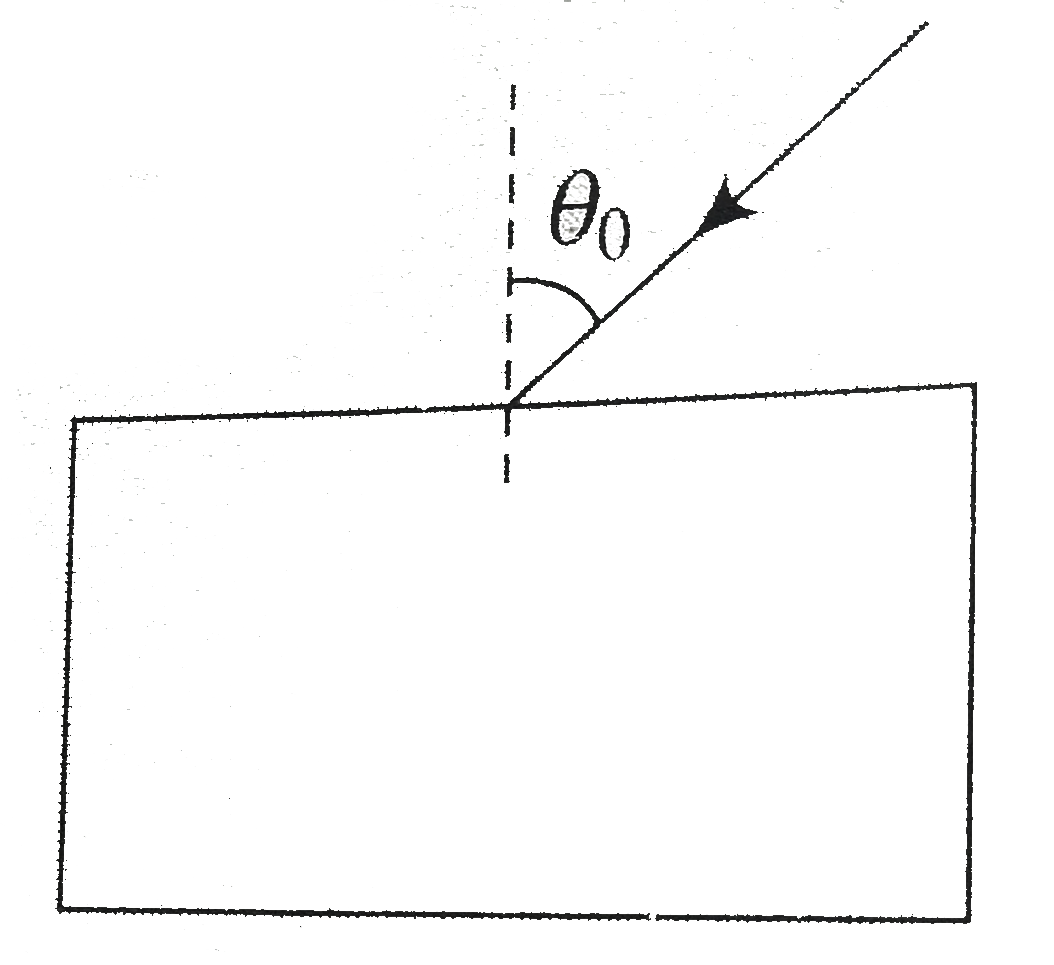
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
 View Solution
View SolutionA jar of height h is filled wih a transparent liquid of refractive index μ, Fig. At the centre of the jar on the botom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.
 .View Solution
.View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
 View Solution
View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied on a 1-kg block. Find the force of interaction of the blocks.

View Solution

