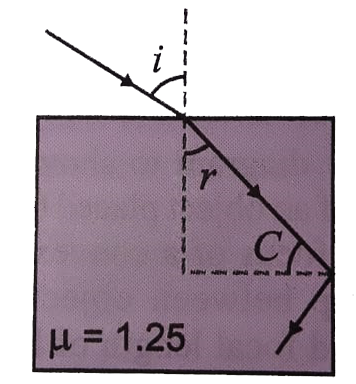
A slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
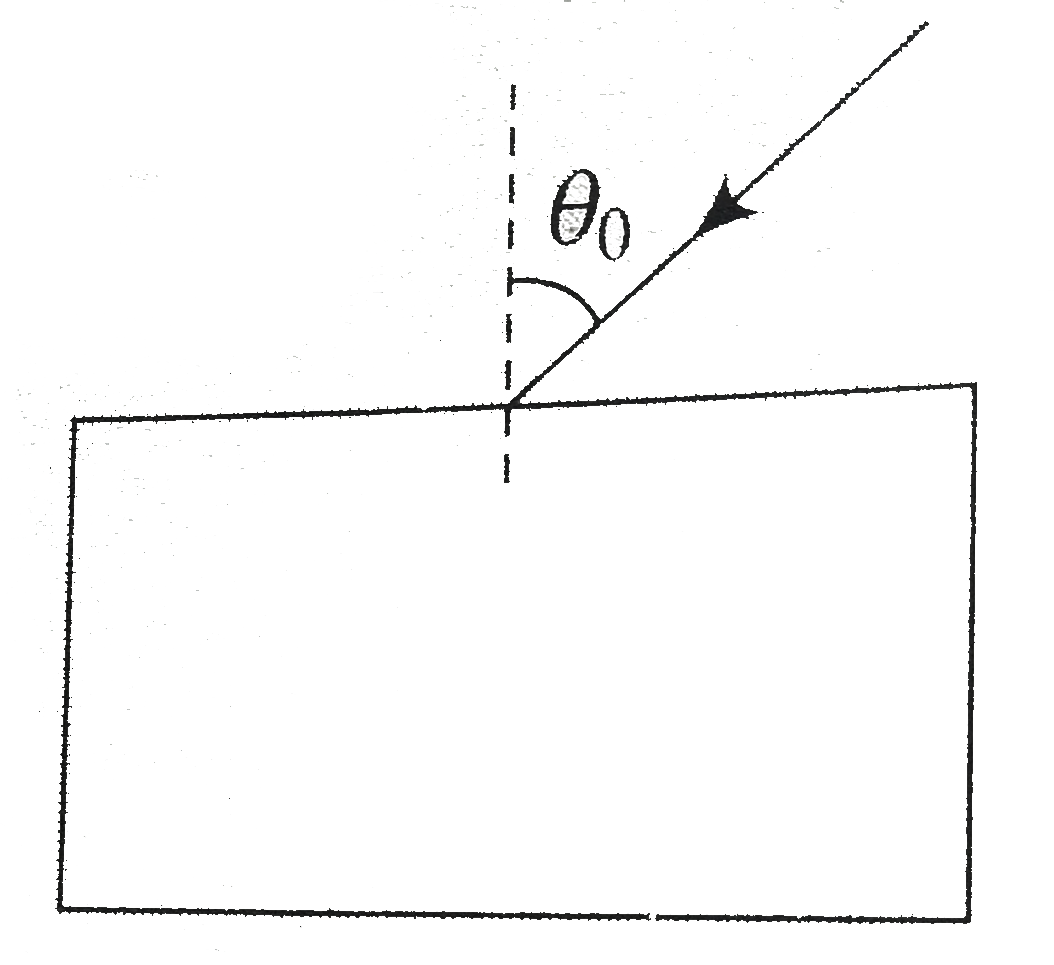
For vertical surface, α>C
⇒sinα>sinC
sinα>1μ (i)
For horizontal surface,
sinθ0=μcosα
⇒sinα=√μ2−sin2θ0μ2 (ii)
From Eqs. (i) and (ii), we get
⇒√μ2−sin2θ0μ>1μ⇒μ2−sin2θ0>1
⇒μ>√1+sin2θ0
So, minimum value of μ=√1+sin2θ0
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
Knowledge Check
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is.
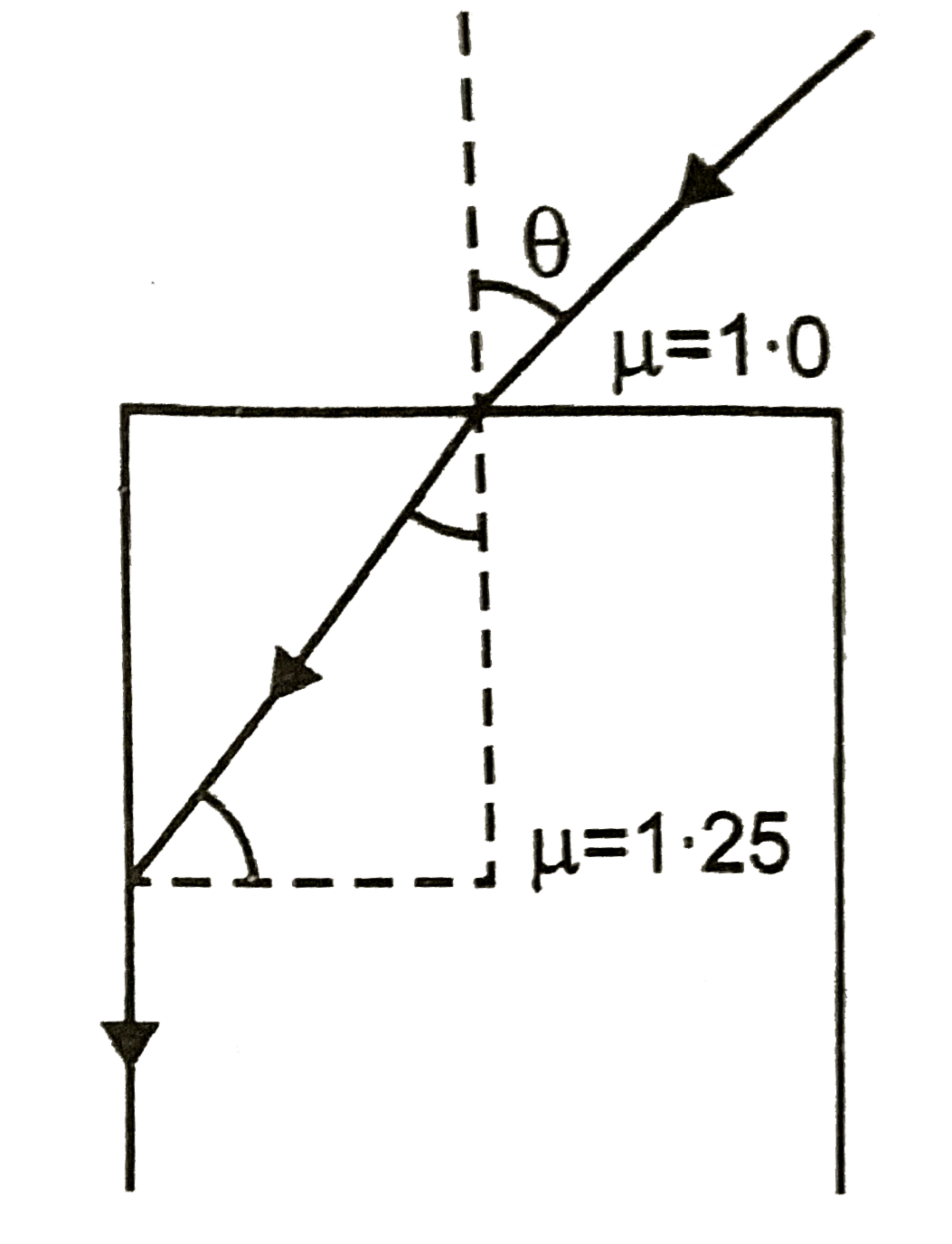 .Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)
.Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is
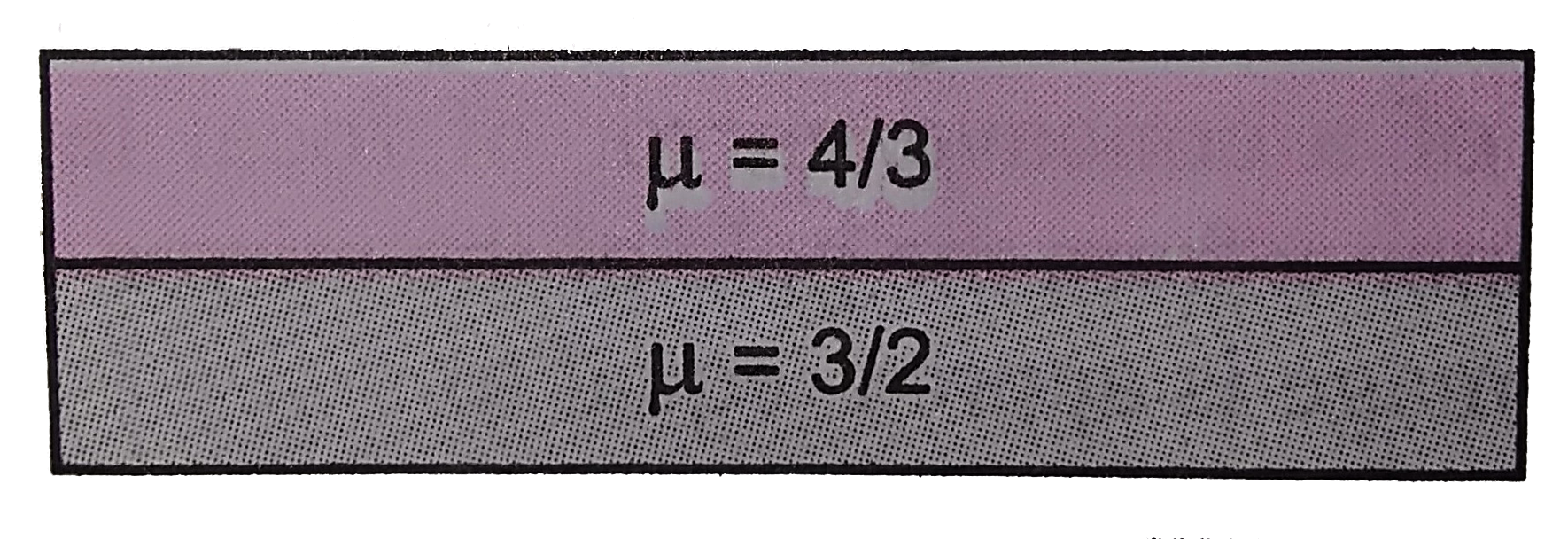 Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)
Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)A cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by
 Asinθ<√n21−n22Bcosθ<√n21−n22Csinθ<1√n21−n22Dcosθ<1√n21−n22
Asinθ<√n21−n22Bcosθ<√n21−n22Csinθ<1√n21−n22Dcosθ<1√n21−n22
Light is incident normally on face AB of a prism as shown in Figure. A liquid of refractive index μ is placed on face AC of the prism. The prism is made of glass of refractive indes 3/2 . Find the limits of μ for which total internal reflection takes place on the face AC.
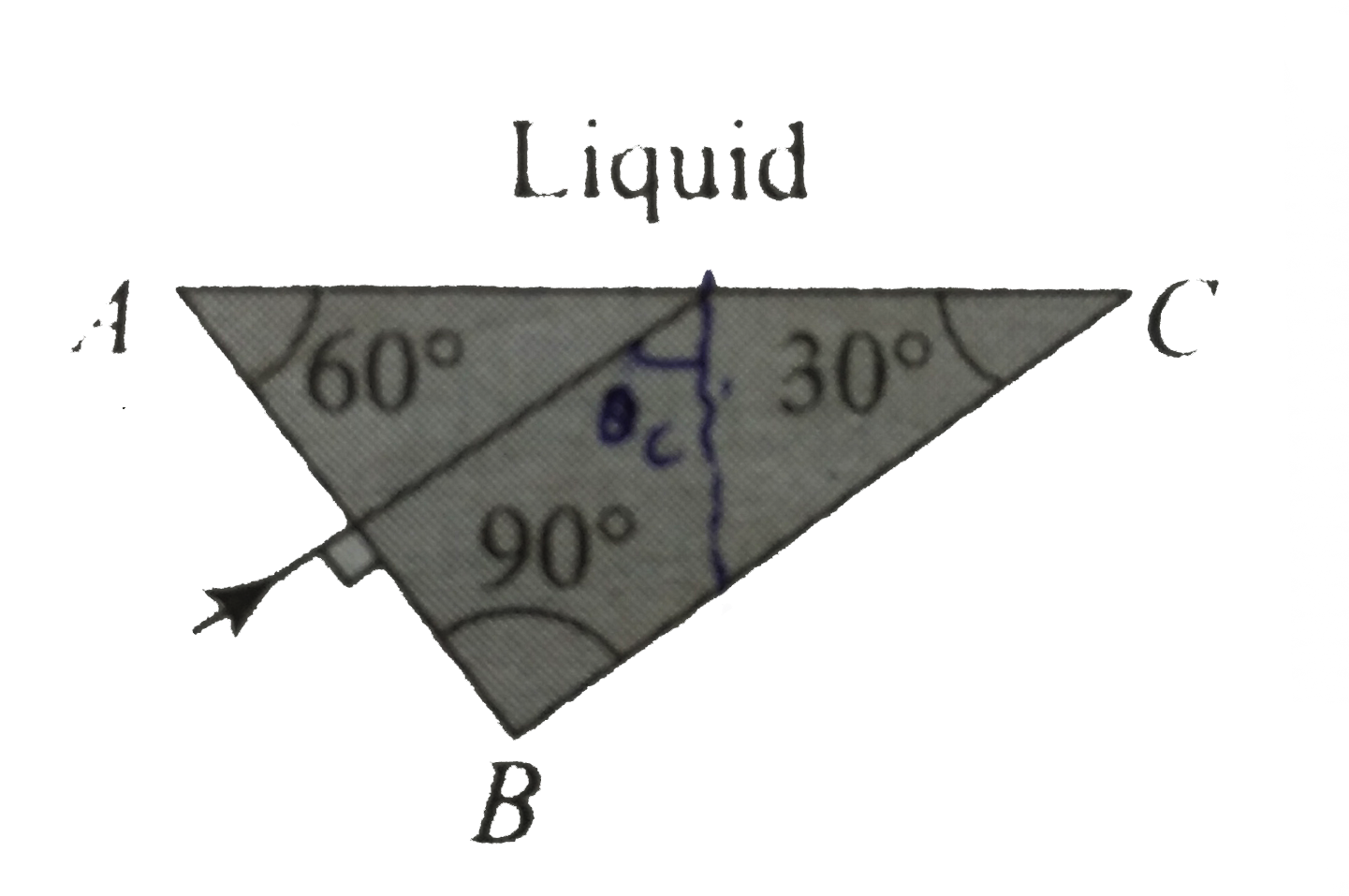
View SolutionConsider the situation shown in figure. Find the maximum angle theta for which the light suffers total internal reflection at the vertical surface.
View SolutionIn the figure shown for an angle of incidence i at the top of the surface, what is the minimum refractive index for total internal reflection at the vertical surface.
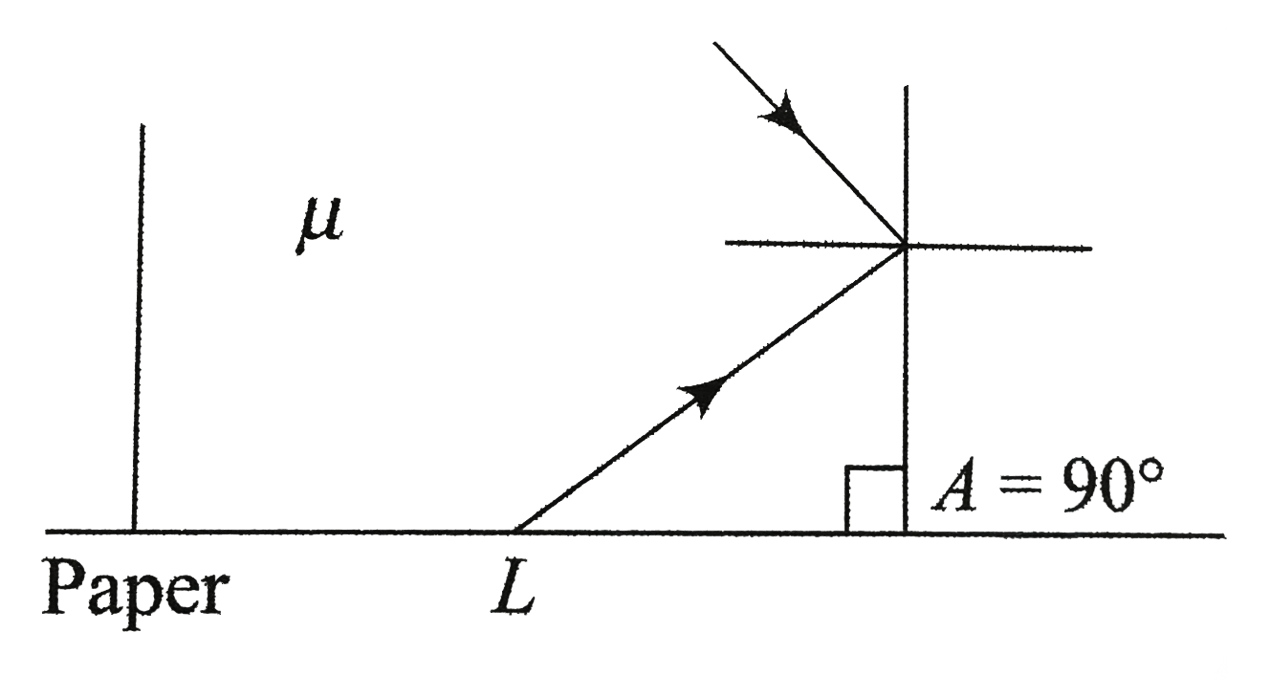
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
View SolutionThe refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
View Solution

 .
.